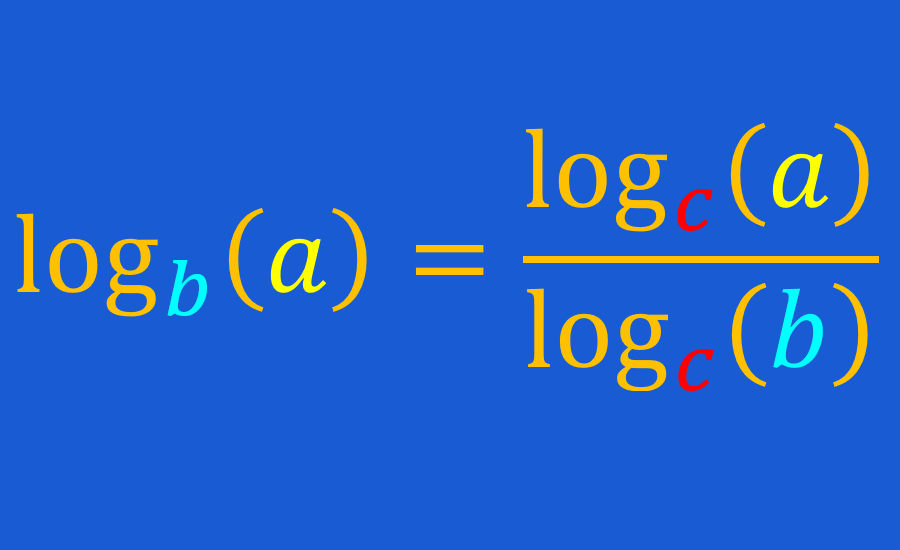La fórmula de cambio de bases de logaritmos puede resultar útil cuando no tenemos calculadoras que nos permitan ingresar logaritmos de cualquier base. Usando esta fórmula podemos reescribir a los logaritmos como una división de logaritmos con la misma base.
A continuación, conoceremos la fórmula de cambio de bases de logaritmos. Además, aprenderemos a aplicar esta fórmula usando varios ejercicios resueltos.
Fórmula de cambio de bases de logaritmos
Tal vez hayas observado que muchas calculadoras solo permiten evaluar logaritmos comunes (de base 10) y logaritmos naturales (de base e). Podemos usar la fórmula de cambio de bases para reescribir a los logaritmos como el cociente de logaritmos de cualquier otra base; cuando usamos una calculadora, podríamos cambiarlos a logaritmos comunes o naturales.
De acuerdo con la fórmula del cambio de base de logaritmos, podemos reescribir a cualquier logaritmo como el cociente de dos logaritmos con una nueva base:
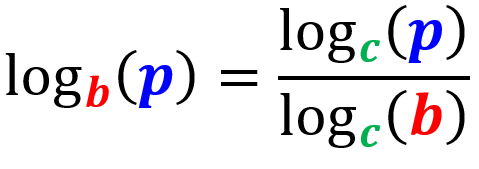
Prueba de la fórmula de cambio de bases
Podemos comprobar que la fórmula de cambio de bases es verdadera al empezar con el logaritmo $latex x=\log_{b}(p)$. Sabemos que los logaritmos y los exponenciales son funciones inversas, por lo que podemos escribir al logaritmo en su forma exponencial:
⇒ $latex {{b}^x}=p$
Ahora, podemos tomar un logaritmo con base “c” a ambos lados de la expresión y tenemos:
$latex \log_{c}({{b}^{x}})=\log_{c}(p)$
Podemos usar la regla de la potencia de logaritmos, la cual nos dice que podemos reescribir de la siguiente manera:
$latex (x)\log_{c}(b)=\log_{c}(p)$
Podemos dividir ambos lados por $latex \log_{c}(b)$ para despejar a x:
$latex x=\frac{\log_{c}(p)}{\log_{c}(b)}$
Ahora, sustituimos el valor de original de x, $latex x=\log_{b}(p)$:
| $latex \log_{b}(p)=\frac{\log_{c}(p)}{\log_{c}(b)}$ |
En términos prácticos, esta fórmula nos dice que podemos evaluar a un logaritmo con una base no estándar al convertirlo en una fracción de la forma “(logaritmo con base estándar del argumento) dividido por (logaritmo con la misma base estándar de la base no estándar)”.
Ejercicios de cambio de bases de logaritmos resueltos
Los siguientes ejercicios ponen en práctica el uso de la fórmula del cambio de bases de logaritmos. Cada ejercicio tiene su respectiva solución, pero es recomendable que intentes resolver los ejercicios tú mismo antes de mirar la respuesta.
EJERCICIO 1
Cambia a $latex \log_{3}(7)$ como un cociente de logaritmos naturales.
Solución
Dado que vamos a expresar al logaritmo como un cociente de logaritmos naturales, la nueva base es e.
Reescribimos al logaritmo como un cociente de logaritmos naturales usando la fórmula de cambio de bases. El numerador del cociente será el logaritmo natural con argumento 7.
El denominador del cociente será el logaritmo natural con argumento 3:
$latex \log_{3}(7)=\frac{\log_{e}(7)}{\log_{e}(3)}$
$latex =\frac{\ln(7)}{\ln(3)}$
EJERCICIO 2
Evalúa $latex \log_{2}(10)$ usando la fórmula de cambio de bases con una calculadora.
Solución
De acuerdo con la fórmula de cambio de bases, podemos escribir al logaritmo base 2 como un logaritmo de cualquier otra base. Dado que las calculadoras sí contienen el logaritmo natural, podemos usar el logaritmo natural:
$latex \log_{2}(10)=\frac{\ln(10)}{\ln(2)}$
$latex \approx 3.3219$
EJERCICIO 3
Convierte a $latex \log_{2}(7)$ como un logaritmo con base 5.
Solución
A pesar de que transformar a un logaritmo con base 5 no sería muy útil para resolver problemas, estos ejercicios están pensados para practicar el uso de la fórmula de cambio de bases. Entonces, tenemos:
$latex \log_{2}(7)=\frac{\log_{5}(7)}{\log_{5}(2)}$
EJERCICIO 4
Evalúa el logaritmo $latex \log_{3}(6)$.
Solución
El argumento es 6 y la base es 3. Podemos usar la fórmula de cambio de bases y cambiar a un cociente de logaritmos naturales:
$latex \log_{3}(6)=\frac{\ln(6)}{\ln(3)}$
$latex =\frac{1.7916}{1.6309}$
Si es que redondeamos a tres decimales, la respuesta final es:
$latex \log_{3}(6)=1.631$
También podríamos usar el logaritmo común:
$latex \log_{3}(6)=\frac{\log(6)}{\log(3)}$
$latex =\frac{0.7782}{0.4771}$
$latex =1.631$
Podemos ver que no importa la base que usemos en la fórmula de cambio de bases. Lo único importante es que mantengamos la misma base tanto en el numerador como en el denominador.
EJERCICIO 5
Simplifica la expresión $latex \frac{\log(625)}{\log(25)}$ para obtener un solo número real.
Solución
En este caso, podemos usar la fórmula de cambio de bases en reverso, es decir, empezamos con el cociente y obtenemos el siguiente logaritmo:
$latex \frac{\log(625)}{\log(25)}=\log_{25}(625)$
Ahora, podemos reescribir a este logaritmo como una potencia para facilitar la resolución. Decimos que el resultado de este logaritmo está dado por la letra x:
$latex {{25}^x}=625$
Podemos reescribir a esto como potencias con la misma base:
$latex {{({{5}^2})}^x}={{5}^4}$
$latex {{5}^{2x}}={{5}^4}$
Dado que las bases son equivalentes, significa que los exponentes también deben ser equivalentes para que la ecuación sea verdadera. Entonces, tenemos:
$latex 2x=4$
$latex x=2$
Por lo tanto, el valor de la expresión original es 2.
Ejercicios de cambio de bases de logaritmos para resolver
Practica lo aprendido sobre la fórmula del cambio de bases con los siguientes ejercicios. Resuelve los ejercicios y selecciona tu respuesta. Verifícala para comprobar que seleccionaste la correcta.
Véase también
¿Interesado en aprender más logaritmos? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
