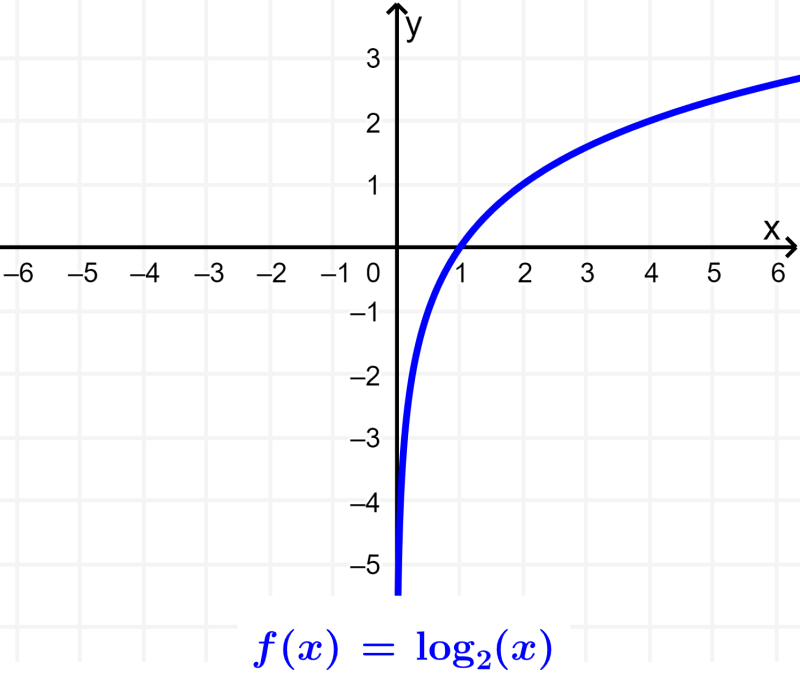
Los logaritmos tienen una gran cantidad de aplicaciones en la vida real. Los logaritmos son especialmente usados para crear escalas de medidas que sean más manejables. Algunos ejemplos de las aplicaciones de los logaritmos incluyen, la escala de Richter para medir terremotos, la escala de decibeles para medir el sonido, los órdenes de magnitud y las aplicaciones en análisis de datos.
A continuación, veremos estas aplicaciones más a detalle.
Órdenes de magnitud
Cuando expresamos algo como “un salario de 6 dígitos”, estamos describiendo a los números dependiendo en cuántas potencias de 10 tienen (están en las decenas, centenas, miles, etc.). Añadir un dígito significa multiplicar por 10. Por ejemplo: el 1 tiene un dígito y el 100 000 tiene seis dígitos.
Los logaritmos cuentan el número de multiplicaciones que son añadidas para obtener un número, Entonces, empezando con el 1 (un solo dígito), añadimos 5 dígitos más $latex ({{10}^5})$ y obtenemos 100 000, un número de seis dígitos.
Los logaritmos nos ayudan a representar números usando escalas más manejables. Resulta más fácil hablar de algo que tiene 6 dígitos en vez de mencionar que tenemos cien mil.
En las computadoras, en donde todo es contado con bits (1 o 0), cada bit tiene un efecto duplicante (no ×10). Entonces, si es que vamos de 8 bits a 16 bits, esto es 8 órdenes de magnitud o $latex {{2}^8}=256$ veces más grande. Cambiando de 16 bits a 32 bits, representa un cambio de 16 órdenes de magnitud o $latex {{2}^{16}}=65536$ veces más grande.
Escala de Richter
La escala de Richter es una escala logarítmica de base 10. Esta escala define la magnitud de un terremoto como el logaritmo de la razón entre la amplitud de las ondas sísmicas con respecto a una amplitud estándar arbitraria:
$latex M=\log(\frac{A}{S})$
en donde, A es la amplitud del terremoto medida con un sismómetro desde aproximadamente 100 km del epicentro del terremoto y S es la amplitud estándar de un terremoto, la cual es definida como 1 micro metro aproximadamente.
Dado que la escala de Richter es una escala logarítmica de base 10, cada incremento de uno en la escala de Richter indica una intensidad diez veces más fuerte que el número previo en la escala.
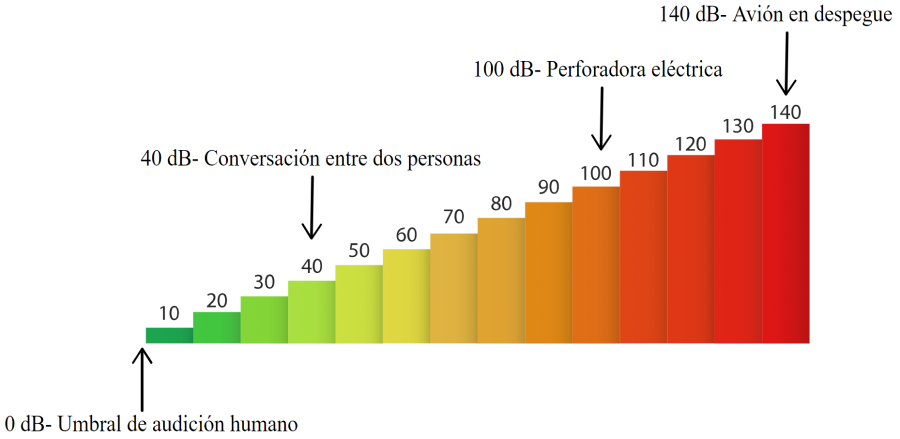
Escala de decibeles
El sonido transporta energía y su intensidad está definida como:
$latex I=\frac{P}{A}$
en donde, P es la potencia, la cual indica la energía que fluye por unidad de área, A, la cual es perpendicular a la dirección en la que la onda de sonido viaja.
La intensidad del sonido es medida en términos del volumen, el cual es medido en términos de un logaritmo. Entonces, la intensidad del sonido es definida como:
$latex \beta=(10dB)\log(\frac{I}{I_{0}})$
En esta definición, dB representa a los decibeles que es igual a un décimo de bel(B). I es la intensidad del sonido y $latex I_{0}$ es la intensidad estándar.
Con los decibeles, podemos representar en la misma escala a intensidades de sonido que varían enormemente en su magnitud.
Aplicaciones en análisis de datos
Los logaritmos son ampliamente usados en el análisis de datos, el cual es a su vez usado en la ciencia de datos y en el aprendizaje automático computacional.
El logit tiene un papel muy importante en la regresión logística. Todas las probabilidades pueden ser convertidas fácilmente a logit.
Las transformaciones logarítmicas también son importantes para facilitar la visualización de patrones en los datos. Usando transformaciones logarítmicas es posible obtener funciones exponenciales que son más fáciles de leer y más entendibles.
Dado que los logaritmos pueden modelar una gran variedad de fenómenos, son extremadamente útiles en la ciencia de datos. Gran parte de la ciencia de datos es el modelamiento de situaciones de la vida real, por lo que las escalas logarítmicas son vitales.
Algoritmo PageRank de Google
Google le da a cada página en la web una puntuación (PageRank), lo cual es aproximadamente una medida de autoridad del sitio web e importancia de la página. Esta es una escala logarítmica, lo que significa que PageRank cuenta el número de dígitos en la puntuación.
Por ejemplo, un sitio con un pagerank de 2 (2 dígitos) es 10 veces más popular que un sitio con un pagerank de 1. El pagerank de CNN es 9, por lo que hay una diferencia es de 4 órdenes de magnitud ($latex {{10}^4}=10000$) en comparación con una página con pagerank de 5.
Véase también
¿Interesado en aprender más sobre logaritmos? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
