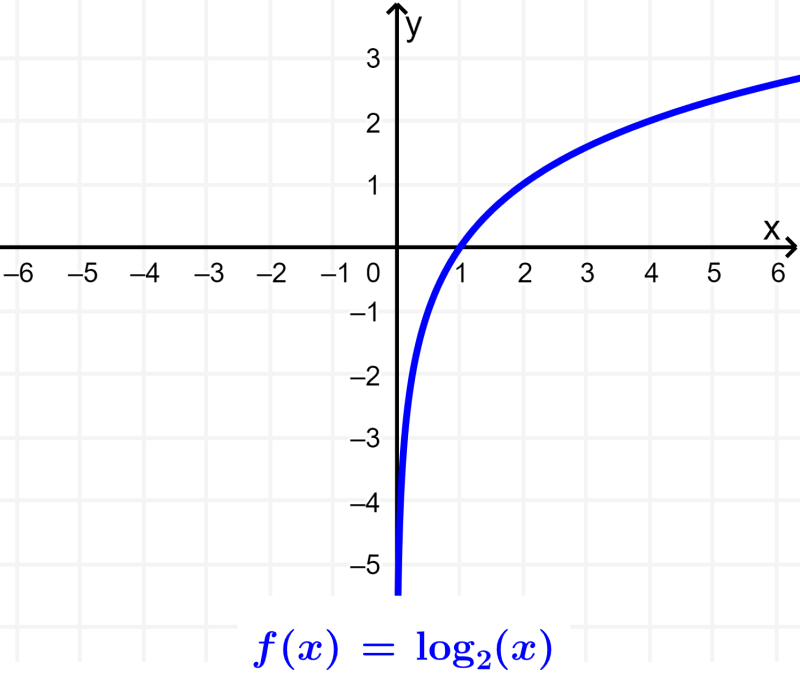
Las propiedades de los logaritmos, también conocidas como leyes de los logaritmos, son útiles ya que nos permiten expandir, condensar o resolver ecuaciones que contienen expresiones logarítmicas.
A continuación, aprenderemos sobre las propiedades y las leyes de los logaritmos. Conoceremos cómo derivar estas propiedades usando las leyes de los exponentes. También, veremos ejemplos de la aplicación de estas propiedades.
Propiedad del producto de logaritmos
La regla del producto de logaritmos indica que la multiplicación de dos o más logaritmos con la misma base puede ser escrita como la suma de los logaritmos individuales:
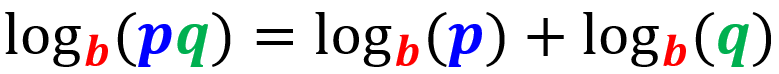
Prueba de esta propiedad
Supongamos que tenemos $latex x=\log_{b}(p)$ y $latex y=\log_{b}(q)$. Podemos escribir cada una de estas ecuaciones a su forma exponencial:
⇒ $latex {{b}^x}=p$
⇒ $latex {{b}^y}=q$
Multiplicando los términos exponenciales p y q, tenemos:
$latex {{b}^x}\times {{b}^y}=pq$
Dado que la base es común, podemos aplicar la regla del producto de exponentes para sumar los exponentes y combinar la base:
$latex {{b}^{x+y}}=pq$
Al tomar el logaritmo con base “b” de ambos lados, tenemos:
$latex \log_{b}({{b}^{x+y}})=\log_{b}(pq)$
Aplicando la regla de la potencia de logaritmos (la cual veremos más adelante), tenemos:
$latex (x+y)\log_{b}(b)=\log_{b}(pq)$
$latex (x+y)=\log_{b}(pq)$
Ahora, sustituimos los valores de x y y en la ecuación obtenida:
| $latex \log_{b}(p)+\log_{b}(q)=\log_{b}(pq)$ |
EJEMPLOS
- Aplicando la propiedad del producto para resolver la expresión $latex \log_{4}(8)+\log_{4}(32)$, tenemos:
$latex \log_{4}(8)+\log_{4}(32)=\log_{4}(8\times 32)$
$latex =\log_{4}(256)$
$latex =4$
- Resolviendo la expresión $latex \log(25)+\log(4)$, tenemos:
$latex \log(25)+\log(4)=\log(25\times 4)$
$latex =\log(100)$
$latex =2$
Propiedad del cociente de logaritmos
La regla o la ley del cociente de logaritmos indica que la razón de dos logaritmos con las mismas bases es igual a la diferencia de los logaritmos
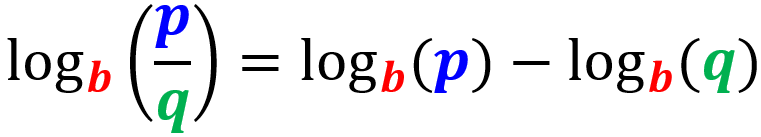
Prueba de esta propiedad
Definamos a las ecuaciones $latex x=\log_{b}(p)$ y $latex y=\log_{b}(q)$. Entonces, podemos reescribirlas en su forma exponencial:
⇒ $latex {{b}^x}=p$
⇒ $latex {{b}^y}=q$
Si es que dividimos los términos exponenciales p y q, tenemos:
$latex \frac{{{b}^x}} {{{b}^y}}=\frac{p}{q}$
Dado que la base es común, aplicamos la regla del cociente de exponentes para combinar la base y restar los exponentes:
$latex {{b}^{x-y}}=\frac{p}{q}$
Ahora, podemos tomar el logaritmo con base “b” de ambos lados:
$latex \log_{b}({{b}^{x-y}})=\log_{b}(\frac{p}{q})$
Si es que aplicamos la regla de la potencia de logaritmos (la cual veremos más adelante), tenemos:
$latex (x-y)\log_{b}(b)=\log_{b}(\frac{p}{q})$
$latex (x-y)=\log_{b}(\frac{p}{q})$
Si es que sustituimos los valores de x y y en la ecuación obtenida, tenemos:
| $latex \log_{b}(p)-\log_{b}(q)=\log_{b}(\frac{p}{q})$ |
EJEMPLOS
- Podemos resolver la expresión $latex \log_{5}(50)-\log_{5}(2)$ con la propiedad del cociente:
$latex \log_{5}(50)-\log_{5}(2)=\log_{5}(\frac{50}{2})$
$latex =\log_{5}(25)$
$latex =2$
- Si es que aplicamos la propiedad del cociente a $latex \log_{3}(108)-\log_{3}(4)$, tenemos:
$latex \log_{3}(108)-\log_{3}(4)=\log_{3}(\frac{108}{4})$
$latex =\log_{3}(27)$
$latex =3$
Propiedad de la potencia de logaritmos
De acuerdo con la propiedad de la potencia de logaritmos, el logaritmo de un número “p” con exponente “n” es igual al producto del exponente con el logaritmo del número (sin el exponente):
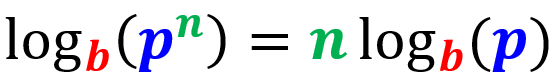
Prueba de esta propiedad
Vamos a definir a la ecuación $latex x=\log_{b}(p)$ y la vamos a reescribir en su forma exponencial:
⇒ $latex {{b}^x}=p$
Podemos elevar a la potencia de n a ambos lados de la ecuación:
$latex {{({{b}^x})}^n}={{p}^n}$
⇒ $latex {{b}^{xn}}={{p}^n}$
Si es que tomamos el logaritmo con base “b” de ambos lados, tenemos:
$latex \log_{b}({{b}^{xn}})=\log_{b}({{p}^n})$
$latex xn\log_{b}(b)=\log_{b}({{p}^n})$
$latex xn=\log_{b}({{p}^n})$
Sustituyendo el valor de x en la ecuación obtenida, tenemos:
| $latex n\log_{b}(p)=\log_{b}({{p}^n})$ |
EJEMPLOS
- Resolvemos la expresión $latex \log_{8}({{64}^2})$ aplicando la propiedad de la potencia de logaritmos:
$latex \log_{8}({{64}^2})=2\log_{8}(64)$
$latex =2(2)$
$latex =4$
- Aplicando la propiedad de la potencia en la expresión $latex \log({{100}^4})$, tenemos:
$latex \log({{100}^4})=4\log(100)$
$latex =4(2)$
$latex =8$
Propiedad de cambio de base de logaritmos
De acuerdo con la propiedad de cambio de base de logaritmos, podemos reescribir a cualquier logaritmo como la razón de dos logaritmos con una nueva base:
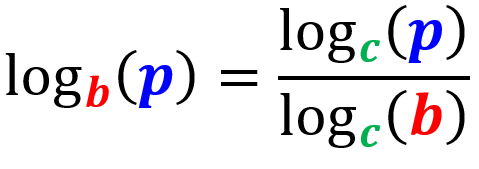
Prueba de esta propiedad
Supongamos que tenemos $latex x=\log_{b}(p)$. Podemos escribir esto en su forma exponencial:
⇒ $latex {{b}^x}=p$
Aplicando el logaritmo con base “c” a ambos lados, tenemos:
$latex \log_{c}({{b}^{x}})=\log_{c}(p)$
Usamos la regla de la potencia de logaritmos:
$latex (x)\log_{c}(b)=\log_{c}(p)$
Ahora, podemos despejar a x:
$latex x=\frac{\log_{c}(p)}{\log_{c}(b)}$
Ahora, sustituimos el valor de x:
| $latex \log_{b}(p)=\frac{\log_{c}(p)}{\log_{c}(b)}$ |
EJEMPLOS
- Aplicamos la propiedad de cambio de bases para resolver $latex \log_{8}(16)$:
$latex \log_{8}(16)=\frac{\log_{2}(16)}{\log_{2}(8)}$
$latex =\frac{4}{3}$
- Resolviendo la expresión $latex \log_{27}(81)$, tenemos:
$latex \log_{27}(81)=\frac{\log_{3}(81)}{\log_{3}(27)}$
$latex =\frac{4}{3}$
Otras propiedades
- El logaritmo de 1 a cualquier base finita diferente de cero es igual a cero.
Prueba de esta propiedad
Podemos probar esto al reescribirla en su forma exponencial:
$latex \log_{b}(1)=0$
⇒ $latex {{b}^0}=1$
- El logaritmo de cualquier número positivo a la misma base es igual a 1.
Prueba de esta propiedad
Nuevamente, podemos probar esto al reescribirla en su forma exponencial:
$latex \log_{b}(b)=1$
⇒ $latex {{b}^1}=b$
Véase también
¿Interesado en aprender más sobre logaritmos y funciones logarítmicas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
