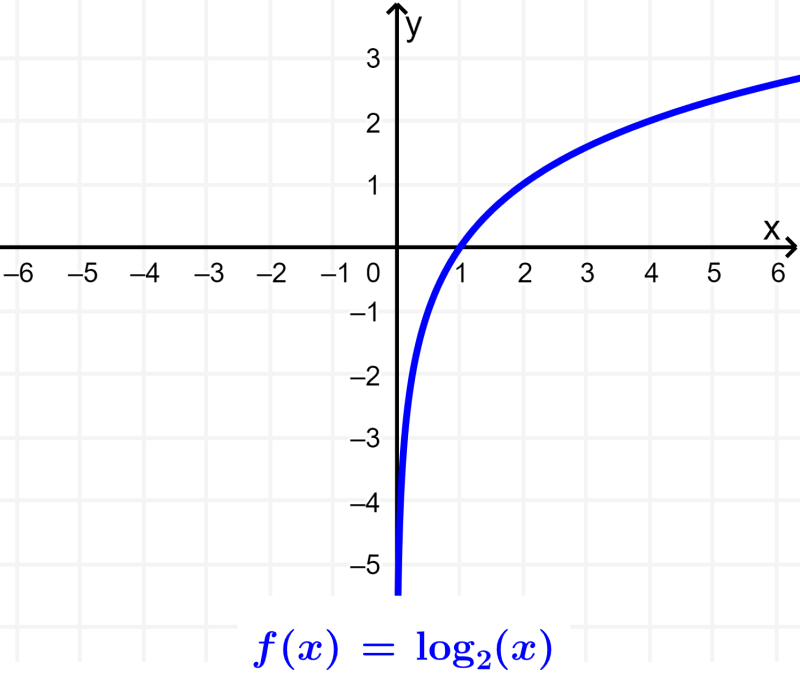
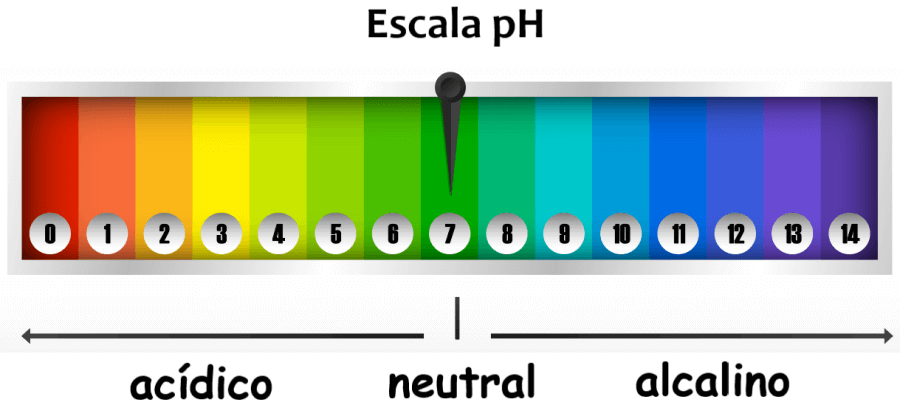
Existen varias aplicaciones de las funciones logarítmicas en la vida cotidiana. Las funciones logarítmicas nos permiten modelar ciertas situaciones de la vida real. Por ejemplo, podemos usar escalas logarítmicas para medir las intensidades de terremotos (escala de Ritcher) y para crear la escala de decibelios del sonido y la escala del pH.
También podemos obtener modelos para la disolución reguladora química y para la entropía de la información.
ÁLGEBRA
Relevante para…
Conocer algunas de las aplicaciones de las funciones logarítmicas.
ÁLGEBRA
Relevante para…
Conocer algunas de las aplicaciones de las funciones logarítmicas.
Aplicaciones importantes de las funciones logarítmicas
Las funciones logarítmicas tienen aplicaciones en varias áreas. Las siguientes son algunas de las más importantes:
Álgebra y Cálculo
Las funciones logarítmicas se utilizan en el cálculo para resolver problemas relacionados con el crecimiento y la disminución exponencial. Por ejemplo, se pueden usar para encontrar la razón de cambio instantánea de una función o para resolver ecuaciones diferenciales que involucran funciones exponenciales.
Física
Las funciones logarítmicas describen fenómenos como la intensidad del sonido y los terremotos. Por ejemplo, la escala de decibelios, que se utiliza para medir la intensidad del sonido, se basa en una función logarítmica.
En sismología, la escala de Richter, que mide la magnitud de los terremotos, también se basa en una función logarítmica.
Ingeniería
Las funciones logarítmicas son usadas para diseñar y analizar circuitos electrónicos, sistemas de control y sistemas mecánicos. Por ejemplo, en ingeniería electrónica, las funciones logarítmicas se utilizan para diseñar y analizar amplificadores, filtros y osciladores.
En los sistemas de control, las funciones logarítmicas se utilizan para modelar el comportamiento de los sistemas y diseñar controladores.
En ingeniería mecánica, las funciones logarítmicas se utilizan para analizar el comportamiento de estructuras y diseñar sistemas mecánicos.
Informática
En informática, las funciones logarítmicas ayudan en el análisis de algoritmos y diseño de algoritmos eficientes. Un ejemplo es el análisis de la complejidad temporal y espacial de los algoritmos.
Muchos algoritmos, como la búsqueda binaria y el algoritmo de clasificación rápida, tienen una complejidad de tiempo logarítmica, lo que los hace muy eficientes para grandes conjuntos de datos.
Economía
El crecimiento económico puede ser analizado con funciones logarítmicas y esto permite analizar las tendencias del mercado. Por ejemplo, se utilizan para modelar el crecimiento del PIB y la propagación de la inflación.
Química
Las funciones logarítmicas pueden ser usadas para describir el comportamiento de las reacciones químicas. Por ejemplo, se utilizan para describir la velocidad de las reacciones químicas, que a menudo se mide en términos del cambio en la concentración de un reactivo o producto a lo largo del tiempo.
Astronomía
Las funciones logarítmicas nos permiten describir el brillo de las estrellas y la distancia de las galaxias. Por ejemplo, la escala de magnitud, que se utiliza para medir el brillo de las estrellas, se basa en una función logarítmica.
Las funciones logarítmicas también se utilizan para estimar la distancia de las galaxias, que puede ser muy grande.
Meteorología
Con el uso de funciones logarítmicas, es posible describir el comportamiento de la presión y la temperatura atmosféricas. Por ejemplo, estas funciones se usan para modelar el comportamiento de la presión atmosférica y la temperatura a diferentes altitudes.
Magnitud de un terremoto
Una de las aplicaciones de las funciones logarítmicas es la medición de las intensidades de los terremotos (escala Ritcher), el sonido (decibeles) y las bases y ácidos (pH). Analicemos la medición de las intensidades de los terremotos.
En 1935 Charles Ritcher definió a la magnitud de un terremoto con la fórmula:
$latex M=\log \left( \frac{I}{S}\right)$
en donde I es la intensidad del terremoto medida por la amplitud de un sismómetro tomada a 100 km del epicentro y S es la intensidad de un terremoto estándar, el cual es definido con una amplitud de 1 micrómetro o $latex {{{10}^{-4}}}$ cm.
Esto significa que la magnitud de un terremoto estándar es:
$latex M=\log \left( \frac{S}{S}\right)=\log (1)=0$
Uno de los terremotos más grandes registrados tuvo una magnitud de 8.9 en la escala de Ritcher. Esto equivaldría a una intensidad de 800 000 000, por lo que la escala de Ritcher nos permite obtener números más manejables.
Cada incremento de un número en la escala de Ritcher indica un aumento de 10 veces en la intensidad. Por ejemplo, un terremoto con una magnitud de 6 es diez veces más fuerte que un terremoto con una magnitud de 5. Un terremoto con una magnitud de 8 es 100 veces más fuerte que un terremoto con una magnitud de 6
EJEMPLO
A comienzos del siglo, un terremoto en California registró 8.3 en la escala de Ritcher. En el mismo año, otro terremoto fue registrado en Sudamérica que fue 4 veces más fuerte. ¿Cuál fue la magnitud del terremoto registrado en Sudamérica?
Solución: Formamos una ecuación con los datos dados en la primera frase:
$latex M_{C}=\log \left( \frac{I_{C}}{S}\right)=8.3$
$latex 8.3=\log \left( \frac{I_{C}}{S}\right)$
Ahora, usamos los datos de la segunda frase para formar la segunda ecuación:
$latex M_{SA}=\log \left( \frac{I_{SA}}{S}\right)$
$latex M_{SA}=\log \left( \frac{4I_{C}}{S}\right)$
Ahora, resolvemos para $latex M_{SA}$:
$latex M_{SA}=\log \left( \frac{4I_{C}}{S}\right)$
$latex =\log (4I_{C})-\log (S)$
$latex =\log (4)+\log (I_{C})-\log (S)$
$latex =\log (4)+(\log (I_{C})-\log (S))$
$latex =\log (4)+\frac{\log (I_{C})}{\log (S)}$
$latex =\log (4)+8.3$
$latex =0.602+8.3$
$latex =8.902$
$latex M_{SA}=8.9$
Entonces, la intensidad del terremoto en Sudamérica fue 8.9 en la escala de Ritcher.
Disolución reguladora química
Sistemas químicos conocidos como disoluciones reguladoras o tampones químicos tienen la habilidad de adaptarse a cambios pequeños en acidad para mantener un rango de valores pH. Las disoluciones reguladoras tienen una gran variedad de aplicaciones desde el mantenimiento de un acuario hasta la regulación de niveles de pH en la sangre.
EJEMPLO
La sangre es una disolución reguladora. Cuando el dióxido de carbono es absorbido en los flujos de sangre, esta produce ácido carbónico y reduce los niveles de pH. El cuerpo compensa produciendo bicarbonato, que es una base débil, para neutralizar el ácido.
La ecuación Henderson-Hasselbalch puede ser usada para calcular el pH de una disolución reguladora. Hasselbalch estaba estudiando el dióxido de carbono que se disuelve en la sangre y el modelo del pH de la sangre en esta situación es $latex \text{pH}=6.1+\log \left( \frac{800}{x} \right)$, en donde x es la presión parcial del dióxido de carbono en las arterias, medida en torr.
Encuentra la presión parcial del dióxido de carbono en las arterias si es que el pH es 7.2.
Solución: Usamos $latex \text{pH}=7.2$ en la ecuación logarítmica dada y obtenemos:
$latex 7.2=6.1+\log \left( \frac{800}{x} \right)$
$latex 1.1=\log \left( \frac{800}{x} \right)$
Al resolver esto para x, encontramos:
$latex x=\frac{800}{{{10}^{1.1}}}=63.55$
Entonces, la presión parcial del dióxido de carbono en las arterias es 63.55 torr.
Entropía de la información
Otra aplicación de las funciones logarítmicas es con la entropía de la información. La entropía de la información H, en bits, de una contraseña generada aleatoriamente que consiste de L caracteres está dada por $latex L\log_{2}(N)$, en donde N es el número de símbolos posibles para cada caracter en la contraseña. En general, entre más grande la entropía, más fuerte es la contraseña.
EJEMPLO
- Si es que una contraseña de 8 caracteres tiene sensibilidad a mayúsculas y minúsculas, es decir, las mayúsculas y minúsculas son consideradas caracteres diferentes, es compuesta sólo de letras y números, encuentra la entropía de la información.
Solución: Hay 27 letras en el abecedario, 54 si es que las mayúsculas y las minúsculas son contadas separadamente. Hay 10 dígitos desde el 0 al 9. Esto es igual a un total de $latex N=63$ símbolos. Dado que la contraseña debe tener 8 caracteres, tenemos $latex L=8$. Entonces:
$latex H=8\log_{2}(64)$
$latex H=\frac{8\ln(64)}{\ln(2)}=48$
- ¿Cuántos símbolos por caracter necesitamos para producir una contraseña de 6 caracteres con una entropía de 40 bits?
Solución: Tenemos $latex L=6$ y $latex H=40$ y tenemos que encontrar N. Entonces, tenemos:
$latex 40=6\log_{2}(N)$
⇒ $latex N={{2}^{\frac{40}{6}}}=101.6$
Entonces, necesitaríamos 102 caracteres para obtener una contraseña con una entropía de 40 bits.
Véase también
¿Interesado en aprender más sobre funciones algebraicas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
