Los ángulos suplementarios son un par de ángulos, los cuales al ser sumados miden 180 grados. Por ejemplo, los ángulos 140° y 40° son suplementarios, ya que al sumarlos obtenemos 180 grados. Cuando unimos a dos ángulos suplementarios, formamos una línea recta.
A continuación, veremos una definición más detallada de los ángulos suplementarios junto con diagramas para ilustrar los conceptos. Además, aprenderemos a encontrar estos ángulos y veremos algunos ejercicios en donde aplicaremos lo aprendido.
¿Qué es un ángulo suplementario?
Los ángulos suplementarios son pares de ángulos tales que la suma de sus ángulos es igual a 180 grados. Estos ángulos siempre vienen en pares, por lo que un ángulo es el suplemento de otro ángulo.
A pesar de que la medida de un ángulo en una línea recta mide 180 grados, no es considerado un ángulo suplementario, ya que no aparece en pares. De igual forma, tampoco podemos tener tres ángulos o más ángulos suplementarios a pesar de que su suma puede ser igual a 180 grados.
EJEMPLOS
Los siguientes son algunos ejemplos de ángulos suplementarios:
- Dos ángulos que miden 90 grados cada uno.
- Ángulos que miden 50 y 130 grados.
- Ángulos que miden 1 y 179 grados.
Podemos tener varios tipos de ángulos suplementarios. Por ejemplo, es posible tener ángulos adyacentes, ángulos no-adyacentes y ángulos rectos.
Ángulos suplemetarios adyacentes
Dos ángulos suplementarios con un vértice común y un segmento común son denominados ángulos suplementarios adyacentes. Un ejemplo de estos ángulos es el siguiente diagrama, en donde los ángulos comparten el segmento OB y también suman 180 grados.
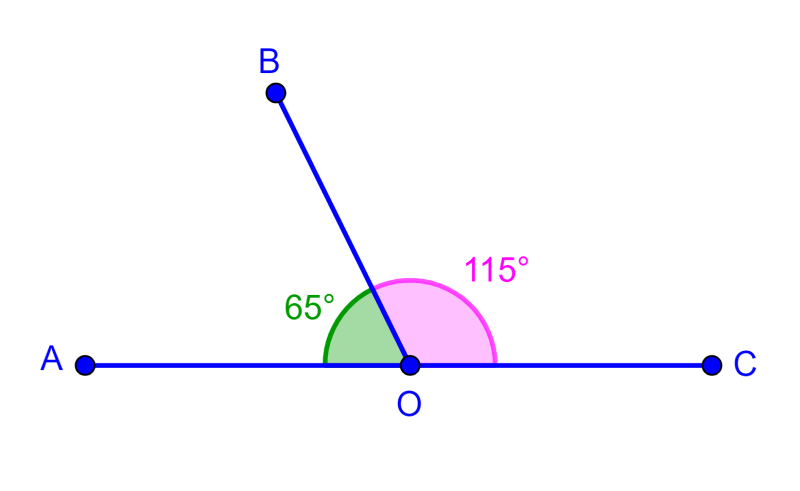
Ángulos suplementarios no-adyacentes
Estos ángulos tienen la característica de ser suplementarios, pero no adyacentes. Esto significa que no comparten un vértice ni un segmento. En el siguiente ejemplo, podemos ver que los ángulos no tiene un vértice común ni un segmento común.
Sin embargo, estos ángulos sí son complementarios, ya que suman 180° y forman una línea recta al unirlos.
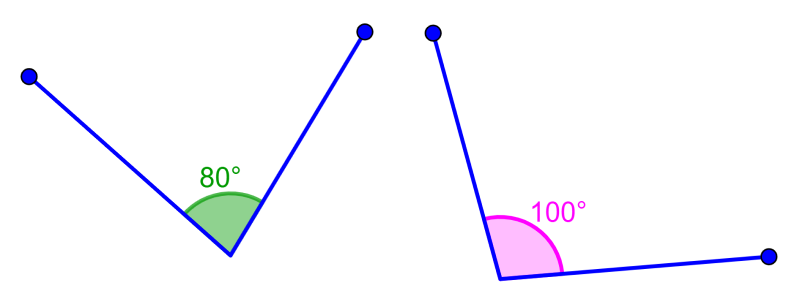
Ángulos suplementarios rectos
Un ángulo suplementario puede ser formado por dos ángulos rectos. Recordemos que los ángulos rectos tienen un ángulo de 90° como en el siguiente diagrama.
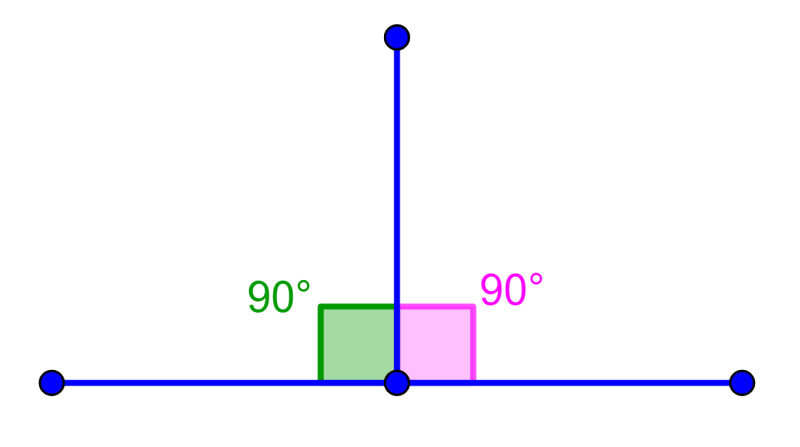
¿Cómo encontrar un ángulo suplementario?
Cuando la suma de dos pares de ángulos es igual a 180 grados, llamamos a ese par de ángulos suplementos el uno del otro. Por lo tanto, sabemos que la suma de dos ángulos suplementarios es 180 grados y cada uno de ellos es denominado un suplemento del otro.
Esto significa que el suplemento de un ángulo es encontrado al restar ese ángulo de 180 grados.
En términos generales, si es que tenemos el ángulo x° su suplemento es (180-x)°. Por ejemplo, el suplemento del ángulo 75° es obtenido al restarlo de 180°. Entonces, su suplemento es (180-75)° = 105°.
Propiedades de ángulos suplementarios
Las siguientes son algunas de las propiedades fundamentales de los ángulos suplementarios:
- Dos ángulos son suplementarios si es que suman 180 grados.
- Tres o más ángulos no pueden ser suplementarios aún si es que suman 180 grados.
- Los ángulos suplementarios pueden ser adyacentes o no-adyacentes.
- Cuando unimos a dos ángulos suplementarios, formamos una línea recta.
- Si es que dos ángulos son suplementarios, cada ángulo es llamado “suplemento” o “ángulo suplementario” del otro ángulo.
Ejercicios de ángulos suplementarios resueltos
Los conceptos aprendidos sobre ángulos suplementarios son aplicados para resolver los siguientes ejercicios. Cada ejercicio tiene su respectiva solución, en donde el proceso y el razonamiento usados son detallados.
EJERCICIO 1
Determina si es que los ángulos 132° y 48° son ángulos suplementarios.
Solución
Sabemos que los ángulos suplementarios suman 180°. Entonces, verificamos si es que los ángulos dados son suplementarios al sumarlos:
132° + 48° = 180°
Vemos que obtuvimos 180°, por lo que los ángulos dados sí son suplementarios.
EJERCICIO 2
Si es que tenemos al ángulo 57°, ¿cuál es su ángulo suplementario?
Solución
Podemos encontrar el ángulo suplementario al restar el ángulo dado de 180°. Entonces, tenemos:
180° – 57° = 123°
El ángulo suplementario a 57° es 123°.
EJERCICIO 3
Encuentra los ángulos suplementarios que tienen una diferencia de 28°.
Solución
Vamos a usar a x para representar a uno de los ángulos. Dado que son suplementarios, el otro ángulo será (180-x)°. La diferencia entre estos ángulos es 28, por lo que tenemos:
(180°-x)-x = 28°
180°-2x = 28°
2x = 152°
x = 76°
⇒ 180°-x = 180°-76°
= 104°
Los dos ángulos suplementarios son 76° y
EJERCICIO 4
¿Cuál es el ángulo suplementario de $latex \frac{2}{3}$ de 120°?
Solución
Tenemos que empezar calculando el ángulo dado:
$latex 120^{\circ}\times \frac{2}{3} =80^{\circ}$
⇒ $latex 180^{\circ}-80^{\circ}=100^{\circ}$
Entonces, el ángulo suplemetario es 100°.
EJERCICIO 5
Encuentra el ángulo que es 68° menos que su suplemento.
Solución
Nuevamente, vamos a usar a la x para representar al ángulo que queremos encontrar. Esto significa que el ángulo suplementario es $latex (180^{\circ}-x)$.
De la pregunta, sabemos que la diferencia entre el ángulo y su suplemento es 68°, por lo que tenemos:
$latex (180-x)-x=68$
$latex 180-2x=68$
$latex -2x=68-180$
$latex -2x=-112$
$latex x=56$
El ángulo es 56°.
Ejercicios de ángulos suplementarios para resolver
Pon en práctica lo aprendido sobre los ángulos suplementarios para resolver los siguientes ejercicios. Si necesitas ayuda con esto, puedes mirar los ejercicios resueltos de arriba.
Véase también
¿Interesado en aprender más sobre ángulos? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
