Los ángulos complementarios están definidos con respecto a la suma de dos ángulos. Tenemos un par de ángulos complementarios cuando la suma de los dos ángulos es igual a 90 grados. En otras palabras, si es que los dos ángulos suman para formar un ángulo recto, estos ángulos son referidos como ángulos complementarios. Aquí, decimos que los dos ángulos se complementan el uno al otro.
A continuación, veremos una definición más detallada de este tipo de ángulos junto con diagramas para ilustrar los conceptos. Además, resolveremos algunos ejercicios en los que aplicaremos las ideas aprendidas.
¿Qué es un ángulo complementario?
Los ángulos complementarios son pares de ángulos que tienen una suma de 90 grados. Al referirnos a estos ángulos, siempre tenemos que recordar que vienen en pares, es decir, un ángulo es el complemento de otro ángulo.
A pesar de que un ángulo recto mide 90 grados, no puede ser llamado un complementario ya que no aparece en pares. Este ángulo es simplemente un ángulo completo. De igual forma, tres ángulos o más ángulos que tienen una suma igual a 90 grados, no pueden ser llamados complementarios.
EJEMPLOS
Los siguientes son ejemplos comunes de ángulos complementarios:
- Dos ángulos que miden 45 grados cada uno.
- Ángulos que miden 30 y 60 grados.
- Ángulos que miden 5 y 85 grados.
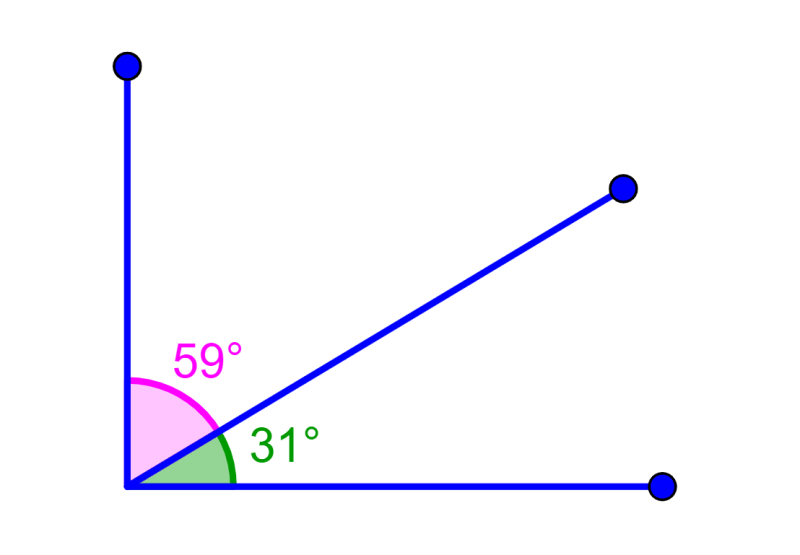
Ángulos complementarios pueden ser ángulos adyacentes. Por ejemplo, en el siguiente diagrama, los ángulos dados son complementarios y adyacentes:
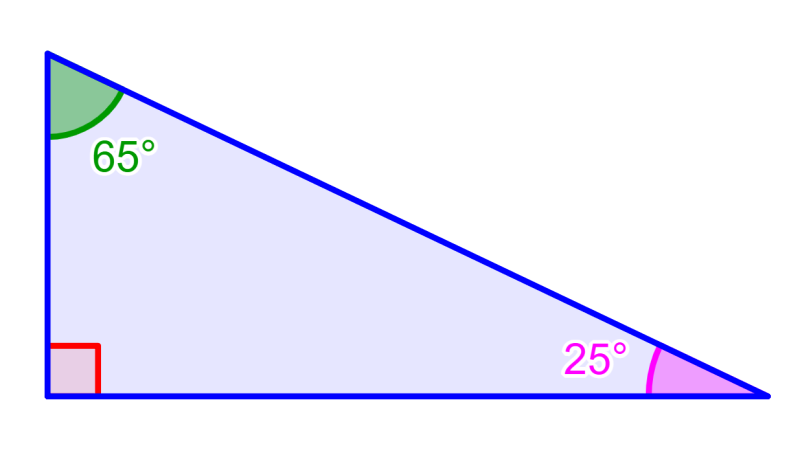
También podemos tener ángulos complementarios que no son adyacentes. Por ejemplo, los ángulos 65° y 25° en el siguiente diagrama son complementarios y no son adyacentes el uno con el otro:
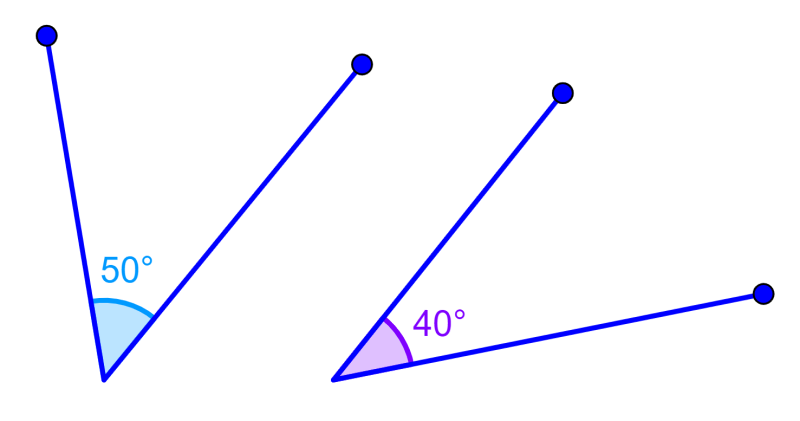
Una propiedad importante de estos ángulos es que no tienen que ser parte de la misma figura necesariamente. Siempre y cuando los ángulos sumen 90 grados, serán complementarios. Por ejemplo, los ángulos en los siguientes diagramas son complementarios, ya que suman 90 grados:
¿Cómo encontrar un ángulo complementario?
Para encontrar ángulos complementarios, tenemos que aplicar las operaciones aritméticas relevantes. Sabemos que la suma de ángulos complementarios es igual a 90 grados y cada uno de ellos es denominado el complemento del otro.
Entonces, el complemento de un ángulo es encontrado al restar al ángulo de 90 grados. En términos generales, si es que tenemos al ángulo x°, su complemento es igual a 90° – x°.
Supongamos que tenemos al ángulo 57° y queremos encontrar su complemento. El complemento del ángulo 57° es obtenido al restarlo de 90°: 90° – 57° = 33°. Entonces, el ángulo complementario de 57° es igual a 33°.
Propiedades de ángulos complementarios
Las siguientes son algunas de las propiedades más importantes de los ángulos complementarios:
- Dos ángulos son complementarios si es que suman 90 grados.
- Los ángulos complementarios pueden ser adyacentes o no-adyacentes.
- Tres o más ángulos no pueden ser complementarios aun si es que su suma es igual a 90 grados.
- Si es que dos ángulos son complementarios, cada ángulo es llamado “complemento” o “ángulo complementario” del otro ángulo.
- Dos ángulos agudos de un triángulo rectángulo son complementarios.
Ejercicios de ángulos complementarios resueltos
Resolvemos los siguientes ejercicios aplicando lo que aprendimos sobre los ángulos complementarios. Cada ejercicio tiene su respectiva solución, en donde el proceso y el razonamiento usados son detallados.
EJERCICIO 1
Calcula el ángulo complementario de 35°.
Solución
Para encontrar el ángulo complementario, restamos el ángulo de 90°:
90° – 35° = 55°
El ángulo complementario de 35° es 55°.
EJERCICIO 2
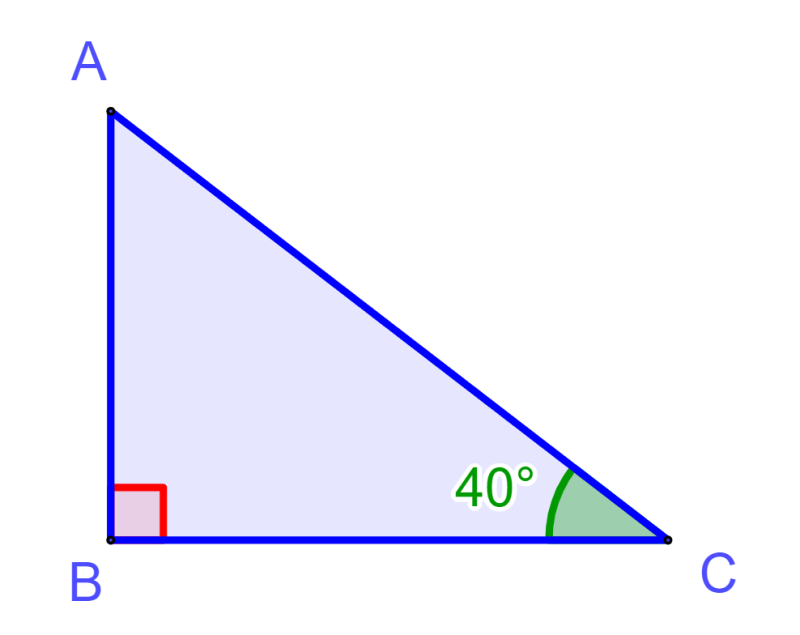
Determina el ángulo faltante de la siguiente figura:
Solución
Sabemos que los ángulos en un triángulo suman 180°, por lo que podemos usar esto y formar la siguiente ecuación:
A + 90° + C = 180°
A + C = 90°
Entonces, sabemos que los ángulos A y C son complementarios ya que deben sumar 90°.
A + 40° = 90°
A = 90° – 40°
A = 50°
EJERCICIO 3
Si es que la diferencia de dos ángulos complementarios es 24°, encuentra los ángulos.
Solución
Podemos usar a x para representar al ángulo pequeño. Esto significa que el ángulo grande será (90-x)°. Entonces, tenemos:
(90°-x)-x = 24°
90°-2x = 24°
2x = 66°
x = 33°
⇒ 90°-x = 90°-33°
= 67°
Los dos ángulos complementarios son 33° y 67°.
EJERCICIO 4
Encuentra el ángulo complementario de 1/3 de 90°.
Solución
Empezamos calculando el ángulo dado:
90/3 =30°
⇒ 90°-30°=60°
Entonces, el ángulo complementario es 60°.
EJERCICIO 5
Encuentra el ángulo que es 38° menos que su complemento.
Solución
Podemos usar a x para representar al ángulo que queremos encontrar, por lo que el ángulo complementario es (90°-x). La pregunta nos dice que la diferencia entre el ángulo y su complemento es igual a 38°. Entonces, tenemos:
(90-x)-x = 38
90-2x = 38
-2x = 38-90
-2x = -38
x = 19
El ángulo es 19°.
Ejercicios de ángulos complementarios para resolver
Usa los siguientes ejercicios para practicar lo aprendido sobre ángulos complementarios. Escoge tu respuesta y haz clic en “Verificar” para comprobar que obtuviste la respuesta correcta.
Véase también
¿Interesado en aprender más sobre ángulos? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
