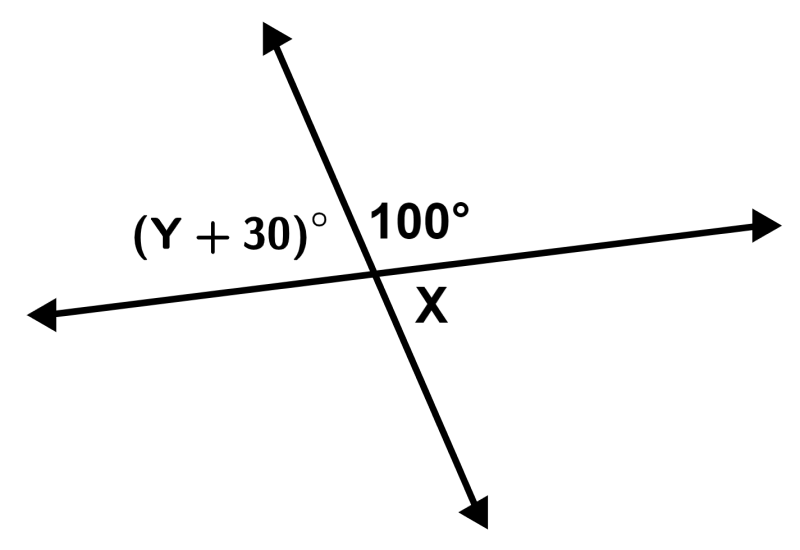Cuando dos líneas se intersecan la una con la otra, entonces, los ángulos opuestos, formados debido a la intersección, son llamados ángulos verticales o ángulos opuestos por el vértice. Un par de ángulos opuestos siempre son iguales el uno con el otro. Además, un ángulo opuesto y su ángulo adyacente son ángulos suplementarios, ya que suman 180 grados.
A continuación, haremos una revisión de lo que significa tener líneas que se intersecan y líneas paralelas. Luego, miraremos los ángulos opuestos por el vértice más a detalle y usaremos diagramas para ilustrarlos. Además, conoceremos el teorema de los ángulos opuestos y resolveremos algunos ejercicios con estos ángulos.
¿Qué son las líneas intersecantes y paralelas?
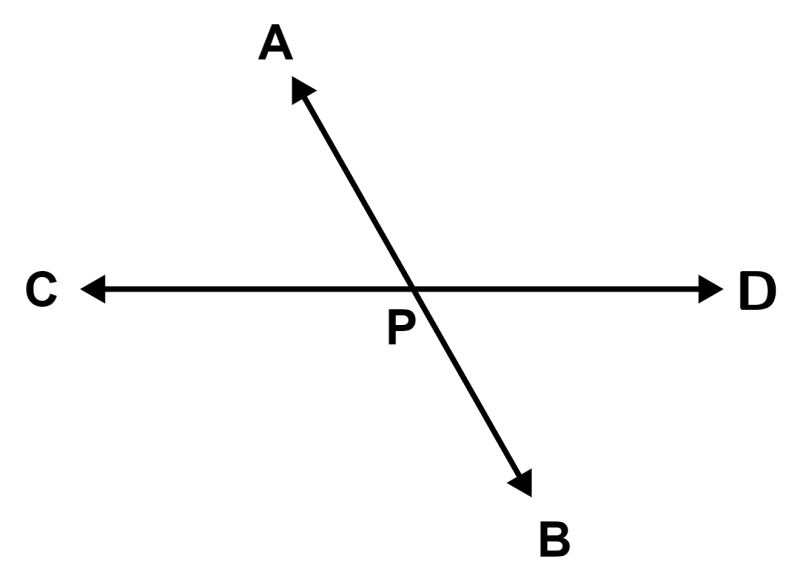
Las líneas intersecantes son líneas que se encuentran o se cruzan la una a la otra en un punto específico. La siguiente es una ilustración de líneas intersecantes:
La línea AB y la línea CD se encuentran en el punto P. Entonces, las dos líneas son líneas intersecantes.
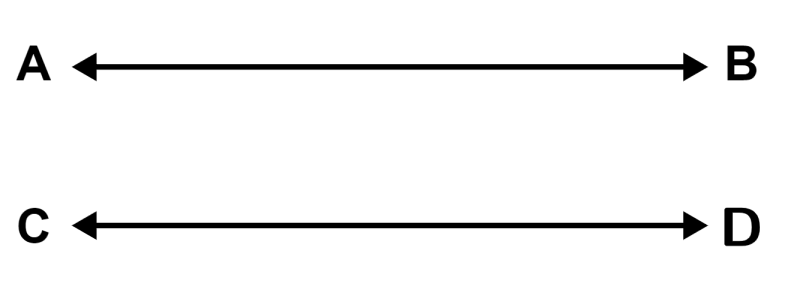
Las líneas paralelas son líneas que no se encuentran en ningún lugar en el plano, tal como tenemos en el siguiente diagrama:
Las líneas AB y CD son paralelas, ya que no se intersecan en ningún punto.
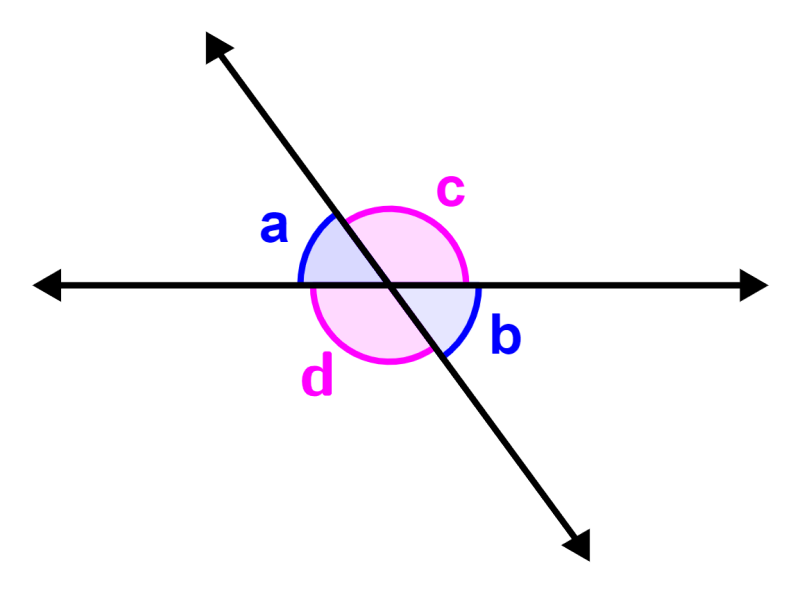
¿Qué son los ángulos opuestos por el vértice?
Los ángulos opuestos son pares de ángulos formados cuando dos líneas se intersecan. Estos ángulos también son denominados ángulos verticales opuestos. Los ángulos opuestos siempre son iguales el uno con el otro.
En general, podemos decir que dos pares de ángulos opuestos son formados cuando dos líneas se intersecan, tal como en el siguiente diagrama:
En este diagrama:
- ∠a y ∠b son ángulos opuestos. Estos ángulos son iguales: ∠a = ∠b.
- ∠c y ∠d son ángulos opuestos. Estos ángulos son iguales: ∠c = ∠d.
Teorema de ángulos opuestos por el vértice
Este teorema indica que, “en un par de líneas intersecantes, los ángulos opuestos por el vértice son iguales”.
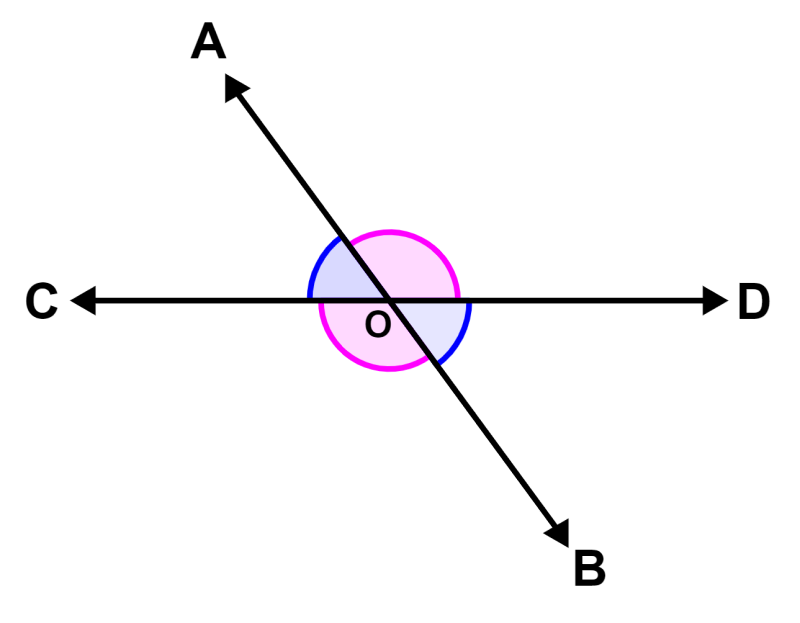
Prueba del teorema: Para comprobar este teorema, consideremos dos líneas AB y CD, las cuales se intersecan en O. Los dos pares de ángulos opuestos son:
- ∠1 y ∠ 2
- ∠3 y ∠4
Podemos ver que el rayo OA se ubica en la línea CD y de acuerdo con el axioma de pares lineales, si es que un rayo se ubica en una línea, los ángulos adycentes forman un par lineal de ángulos. Entonces, tenemos:
∠1 + ∠3 = 180° (par lineal)
De igual forma el rayo OD se ubica en la línea AB, por lo que también tenemos:
∠3 + ∠2 = 180° (par lineal)
Si es que combinamos estas dos ecuaciones, tenemos:
∠1 + ∠3 = ∠3 + ∠2
∠1 = ∠2
Entonces, el par de ángulos opuestos son iguales. Podemos usar el mismo proceso para demostrar esto con el otro par de ángulos opuestos.
Ejercicios de ángulos opuestos por el vértice resueltos
Las propiedades de los ángulos opuestos pueden ser usadas para resolver los siguientes ejercicios.
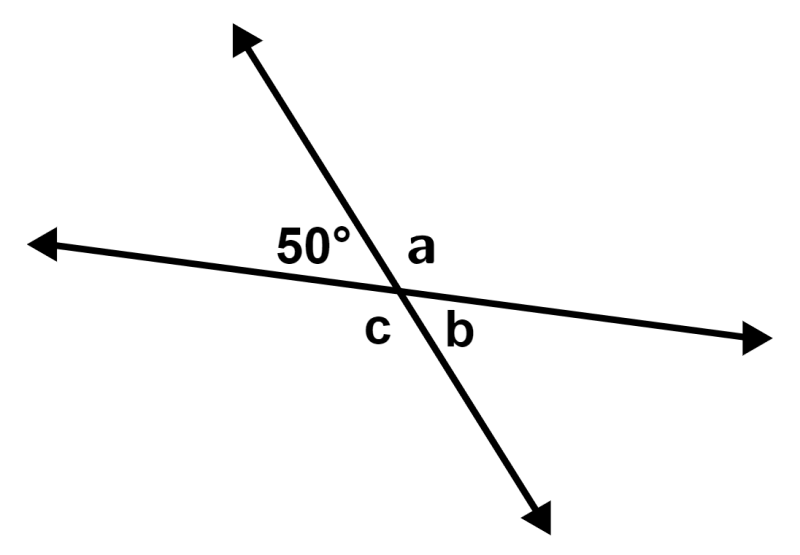
EJERCICIO 1
Calcula los ángulos faltantes en la siguiente figura:
Solución: Los ángulos ∠50° y ∠b son ángulos verticales opuestos, por lo que son iguales y tenemos:
∠b = 50°
Los ángulos ∠50° y ∠a son ángulos suplementarios, por lo que tenemos:
50°+∠a = 180°
∠a = 130°
Los ángulos ∠a y ∠c son opuestos, por lo que tenemos:
∠c = 130°
EJERCICIO 2
Calcula el valor de Y en la siguiente figura:
Solución: Los ángulos ∠100° y ∠X son suplementarios, por lo que tenemos:
100°+∠X = 180°
∠X = 80°
Sabemos que los ángulos (Y+30)° y X son verticales opuestos, por lo que tenemos:
Y+30 = 80
Y = 50°
EJERCICIO 3
Si los ángulos (4a-19)° y (3a+16)° son ángulos verticales opuestos, ¿cuál es el valor de a?
Solución: Dado que los ángulos son verticales opuestos, sabemos que son iguales:
4a-19 = 3a+16
4a-3a = 16+19
a = 35
El valor de los ángulos dados es:
4(35)-19 = 121°
EJERCICIO 4
Si es que tenemos que los ángulos (2x+5)° y (3x-25)° son consecutivos, ¿cuál es su medida?
Solución: Los ángulos consecutivos son suplementarios, por lo que tenemos:
(2x+5) + (3x-25) = 180
5x-20 = 180
5x = 200
x = 40
Entonces, la medida de los ángulos es:
2x+5 = 2(40)+5 = 85°
3x-25 = 3(40)-25 = 95°
Véase también
¿Interesado en aprender más sobre ángulos? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
