Los ángulos alternos internos son los ángulos formados cuando una transversal interseca dos líneas paralelas o no-paralelas. Estos ángulos se ubican en la parte interna de las líneas paralelas, pero en los lados opuestos de la transversal. La transversal cruza a través de las dos líneas, las cuales son coplanares, en puntos diferentes. Estos ángulos representan si es que las dos líneas dadas son paralelas la una a la otra o no. Si es que estos ángulos son iguales el uno al otro, entonces, las líneas cruzadas por la transversal son paralelas.
A continuación, exploraremos a estos ángulos más a detalle. Usaremos diagramas para ilustrar los conceptos y conoceremos algunas de sus propiedades más importantes. Además, aprenderemos sobre el teorema de ángulos alternos internos y veremos su prueba. Finalmente, resolveremos algunos ejercicios relacionados a estos ángulos.
¿Qué son los ángulos alternos internos?
Los ángulos alternos internos son ángulos formados cuando dos líneas paralelas o no-paralelas son intersecadas por una transversal. Estos ángulos están ubicados en las esquinas internas de las intersecciones y están en lados opuestos de la transversal.
Estos ángulos son iguales si es que las líneas intersecadas por la transversal son paralelas. Por otra parte, los ángulos alternos internos formados cuando una transversal cruza dos líneas no-paralelas no tienen ninguna relación geométrica.
Consideremos el siguiente diagrama:
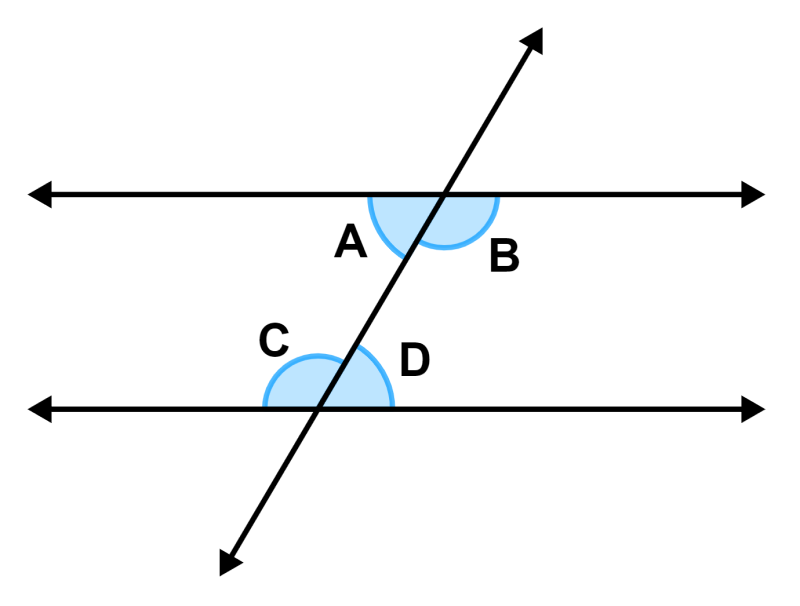
Podemos ver que las dos líneas paralelas son intersecadas por una transversal. Esto significa que los ángulos alternos dentro de las líneas paralelas serán iguales. Es decir, tenemos:
∠A = ∠D y ∠B = ∠C
Propiedades de los ángulos alternos internos
Las siguientes son algunas de las propiedades importantes de los ángulos alternos internos:
- Si es que las dos líneas son paralelas, los ángulos son congruentes.
- Ángulos internos consecutivos son suplementarios, es decir, suman 180°.
- En el caso de líneas no-paralelas, los ángulos alternos internos no tienen propiedades específicas.
Teorema de ángulos alternos internos
Este teorema indica que, “si es que una transversal cruza a dos líneas paralelas, los ángulos alternos internos son congruentes”. Para comprobar este teorema, consideremos el siguiente diagrama:
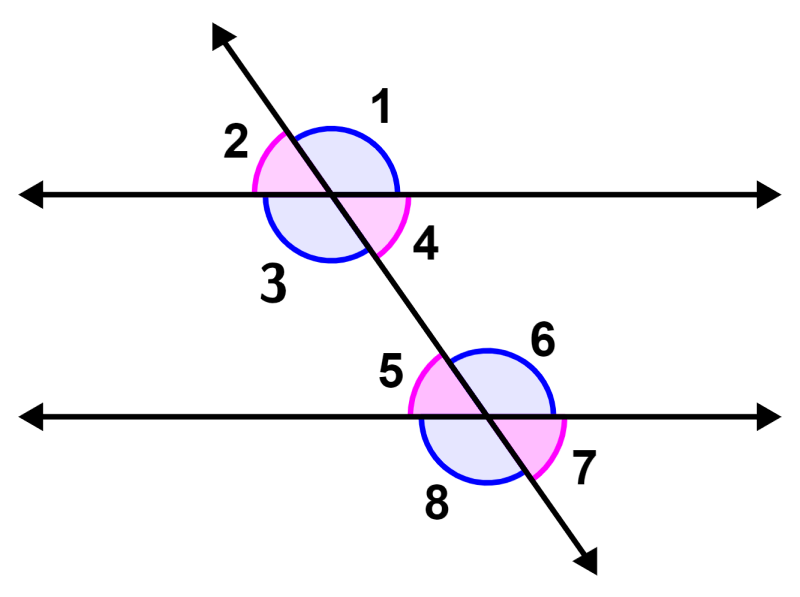
De las propiedades de las líneas paralelas, sabemos que si es que una transversal cruza a través de dos líneas paralelas, los ángulos correspondientes y los ángulos verticales opuestos son iguales el uno con el otro. Entonces, tenemos:
∠2 = ∠5 (ángulos correspondientes)
∠2 = ∠4 (ángulos verticales opuestos)
De estas dos igualdades, podemos concluir que:
∠4 = ∠5 (ángulos alternos internos)
De igual forma, también tenemos:
∠3 = ∠6 (ángulos alternos internos)
Ángulos co-internos
Los ángulos co-internos son los ángulos que están en el mismo lado de la transversal. Los ángulos co-internos suman 180°. Esto significa que los ángulos internos, que están en el mismo lado de la transversal, son suplementarios.
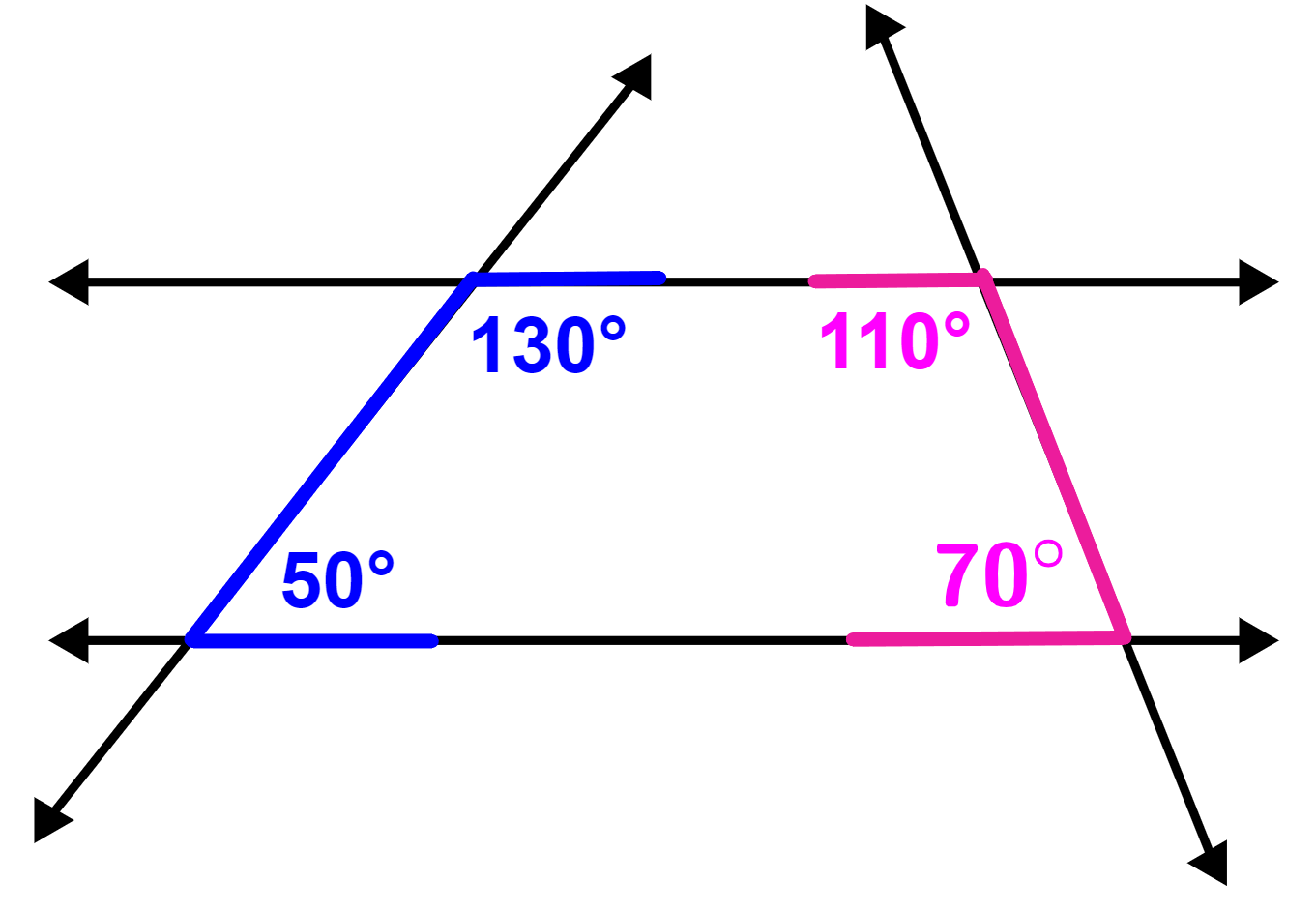
Los ángulos co-internos tienen la forma de una “C” y estos ángulos no son iguales el uno con el otro. Estos ángulos también son conocidos como los ángulos consecutivos internos o los ángulos internos del mismo lado.
Ejercicios de ángulos alternos internos resueltos
Los ejercicios de ángulos alternos internos pueden ser resueltos usando las propiedades de las líneas paralelas.
EJERCICIO 1
Encuentra el valor de B y D en la siguiente figura:
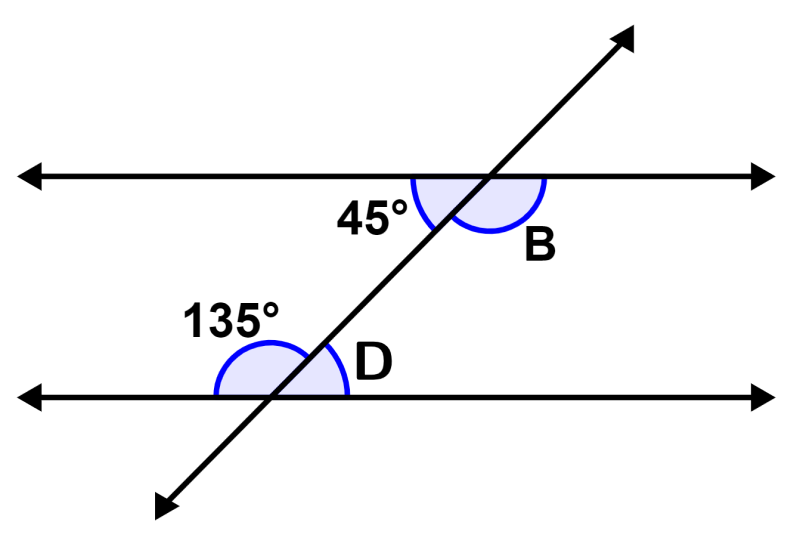
Solución: Dado que el ángulo de 45° y D son ángulos alternos internos, sabemos que son congruentes, por lo que tenemos:
D = 45°
De igual forma, el ángulo de 135° y B son ángulos alternos internos, por lo que tenemos:
B = 135°
EJERCICIO 2
Encuentra el valor de A, C y D en la siguiente figura:
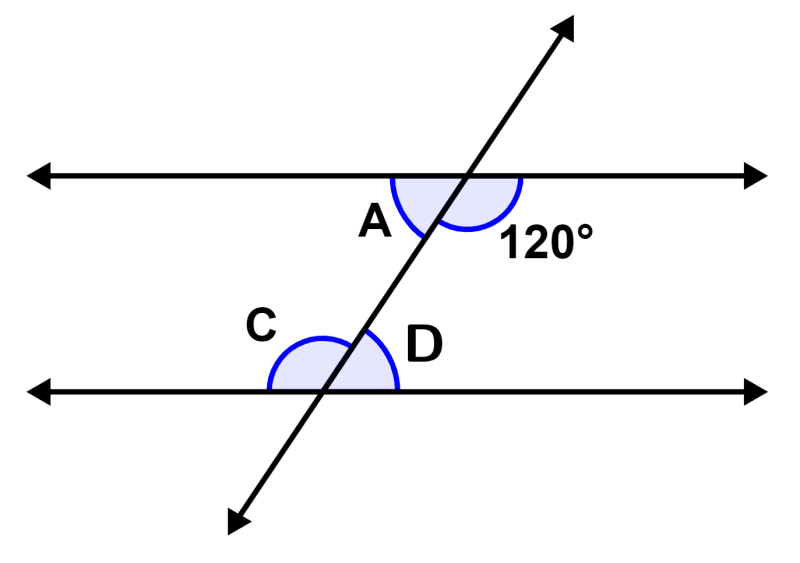
Solución: Los ángulos ∠A, 120°, ∠C y ∠D son ángulos internos, por lo que sabemos que tenemos:
∠C = 120°
Por el teorema de ángulos suplementarios, sabemos que tenemos:
∠C+∠D = 180°
∠D = 180° – ∠C = 180° – 120° = 60°
EJERCICIO 3
Si es que tenemos que los ángulos (4x-19)° y (3x+16)° son ángulos alternos internos congruentes, ¿cuál es el valor de x?
Solución: Los ángulos son congruentes, por lo que tenemos:
4x-19 = 3x+16
4x-3x = 16+19
x = 35
Esto significa que los ángulos dados son iguales a:
4(35)-19 = 121°
EJERCICIO 4
Dos ángulos internos consecutivos son (2x+10)° y (x+5)°. Encuentra la medida de los ángulos.
Solución: Los ángulos internos consecutivos son suplementarios, por lo que tenemos:
(2x+10) + (x+5) = 180
3x+15 = 180
3x = 165
x = 55
Entonces, los ángulos internos consecutivos son:
2x+10 = 2(55)+10 = 120°
x+5 = 55+5 = 60°
Véase también
¿Interesado en aprender más sobre ángulos? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
