Los ángulos alternos externos son un par de ángulos formados en la parte exterior de dos líneas que son cruzadas por una tercera línea. Los ángulos alternos se ubican en lados opuestos de la línea transversal. Dependiendo en la naturaleza de las líneas, los ángulos tendrán algunas características. Por ejemplo, si es que las dos líneas son paralelas, los ángulos alternos externos serán iguales.
A continuación, exploraremos a este tipo de ángulos más a detalle. Ilustraremos los conceptos usando diagramas y conoceremos las propiedades fundamentales de estos ángulos. También, aprenderemos sobre el teorema de ángulos alternos externos y veremos algunos ejercicios resueltos.
¿Qué son los ángulos alternos externos?
Los ángulos alternos externos son ángulos creados cuando tres líneas se intersecan. Cuando una línea transversal cruza a las otras dos líneas, crea un exterior y un interior para las líneas paralelas. Estos ángulos son creados en el espacio afuera de las líneas paralelas en lados alternos.
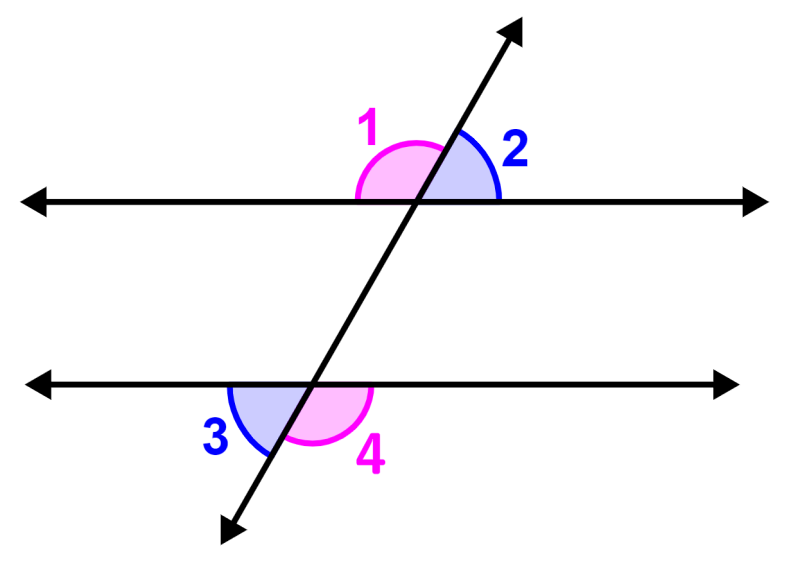
En el siguiente diagrama, tenemos dos líneas paralelas que son cruzadas por una línea transversal. Podemos enumerar los vértices exteriores de la siguiente manera:
Entonces, tenemos los cuatro ángulos exteriores:
- ∠1
- ∠2
- ∠3
- ∠4
Los ángulos alternos externos son pares que aparecen afuera de las líneas cruzadas y en diferentes líneas. En este caso, los ángulos alternos externos son:
- ∠1 y ∠4
- ∠2 y ∠3
Propiedades de los ángulos alternos externos
Las siguientes son las propiedades fundamentales de los ángulos alternos externos:
- Cuando las dos líneas son paralelas, los ángulos alternos externos son congruentes (tienen la misma medida).
- Los ángulos externos consecutivos son suplementarios (suman 180°).
- Cuando las dos líneas son no-paralelas, los ángulos alternos externos no tienen propiedades específicas.
Teorema de ángulos alternos externos
Cuando dos líneas son paralelas, la transversal crea ángulos alternos externos. El teorema dice: “Si es que un par de líneas paralelas son cruzadas por una transversal, entonces, los ángulos alternos externos son congruentes “.
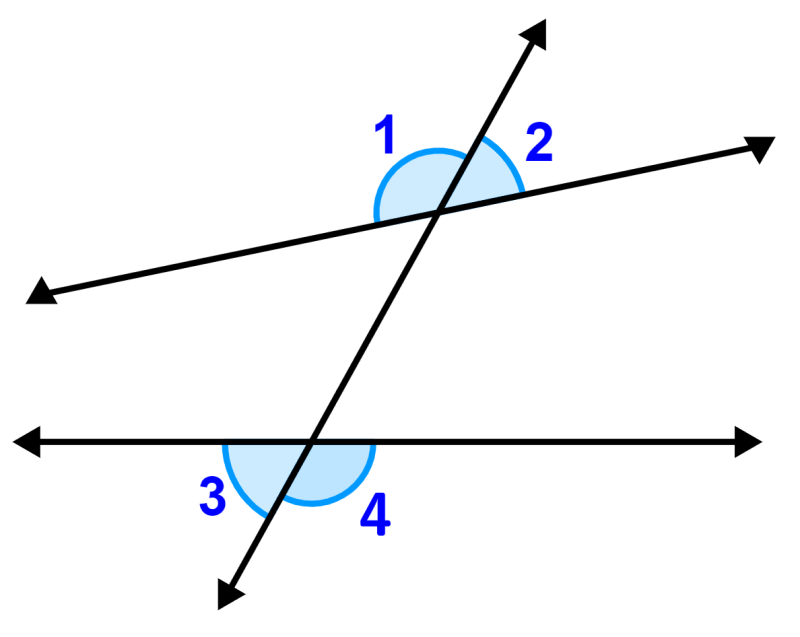
En el siguiente diagrama, tenemos un par de líneas paralelas que son cruzadas por una transversal.
Tenemos los mismos ángulos externos:
- ∠1
- ∠2
- ∠3
- ∠4
Usando el teorema de ángulos alternos externos, sabemos que los ángulos alternos externos formados por líneas paralelas son congruentes, por lo que tenemos:
- ∠1 = ∠4
- ∠2 = ∠3
Teorema inverso de ángulos alternos externos
Lo opuesto del teorema de ángulos alternos externos también es verdadero: “Si es que los ángulos alternos externos de dos líneas cruzadas por una transversal son congruentes, entonces, las líneas son paralelas”.
Entonces, si es que tenemos que los ángulos ∠1 y ∠4 son iguales, automáticamente sabemos que las líneas deben ser paralelas.
Ejercicios de ángulos alternos externos resueltos
Podemos usar las propiedades de los ángulos alternos externos para resolver algunos ejercicios.
EJERCICIO 1
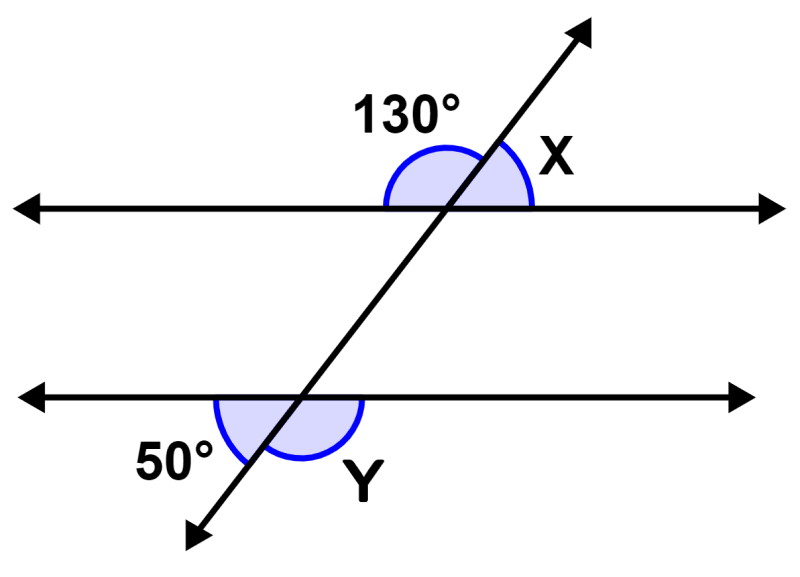
¿Cuál es el valor de X y Y en la siguiente figura?
Solución: Los ángulos 50° y Y son ángulos alternos externos. Dado que las líneas son paralelas, sabemos que tenemos:
Y = 50°
Similarmente, los ángulos 130° y Y son ángulos alternos externos, por lo que tenemos:
X = 130°
EJERCICIO 2
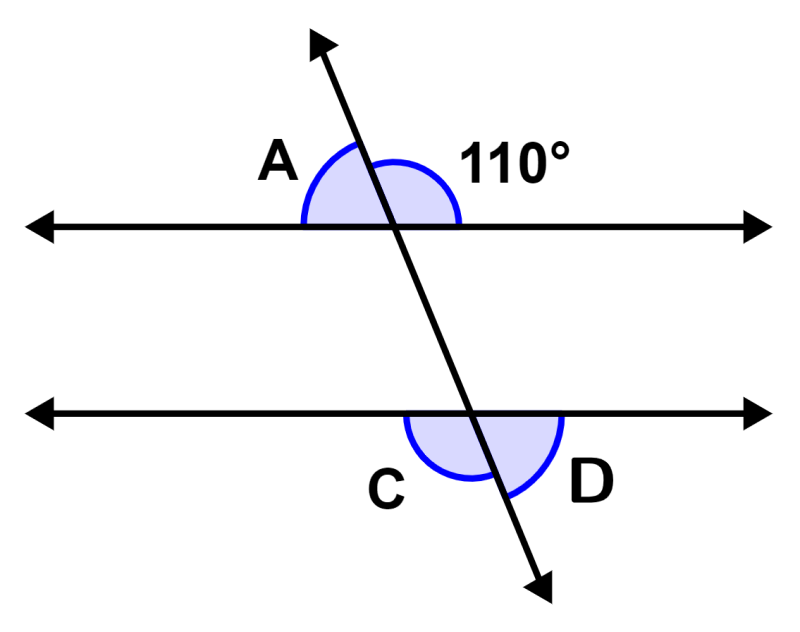
¿Cuál es el valor de los ángulos faltantes en el diagrama?
Solución: Los ángulos ∠A, 110°, ∠C y ∠D son ángulos externos. Dado que las líneas son paralelas, tenemos:
∠C = 110°
Además, sabemos que los ángulos consecutivos son suplementarios, por lo que tenemos:
∠C+∠D = 180°
∠D = 180° – ∠C = 180° – 110° = 70°
EJERCICIO 3
Tenemos que los ángulos (5x-25)° y (3x+35)° son ángulos alternos externos congruentes. ¿Cuál es el valor de x?
Solución: Sabemos que los ángulos congruentes tienen la misma medida, por lo que tenemos:
5x-25 = 3x+35
5x-3x = 25+35
2x = 60
x = 30
Entonces, los ángulos dados son:
5(30)-25 = 125°
EJERCICIO 4
Tenemos los ángulos externos consecutivos (3x-10)° y (x+30)°. Encuentra la medida de los ángulos.
Solución: Sabemos que los ángulos externos consecutivos son suplementarios, por lo que podemos formar la siguiente ecuación:
(3x-10) + (x+30) = 180
4x+20 = 180
4x = 160
x = 40
Entonces, los ángulos son:
3x-10 = 3(40)-10 = 110°
x+30 = 40+30 = 70°
Véase también
¿Interesado en aprender más sobre ángulos? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
