Antes de empezar con los ángulos correspondientes directamente, tenemos que hacer una breve revisión de los ángulos, de las líneas paralelas y no-paralelas y de las líneas transversales.
En geometría, un ángulo está compuesto por tres partes: un vértice y dos lados o segmentos. El vértice de un ángulo es el punto en el que dos lados o líneas del ángulo se encuentran, mientras que los lados son simplemente los segmentos de líneas.
Las líneas paralelas son dos o más líneas en el plano 2D que nunca se cruzan. Estas líneas tienen la misma pendiente. Por otra parte, las líneas no-paralelas son dos o más líneas que se intersecan. Una línea transversal es una línea que pasa a través de dos líneas paralelas o no-paralelas.
¿Qué son los ángulos correspondientes?
Los ángulos correspondientes son ángulos formados cuando una línea transversal cruza a dos líneas rectas. Estos ángulos son formados en esquinas equivalentes o en esquinas correspondientes con la transversal cuando dos líneas son intersecadas por una tercera línea.
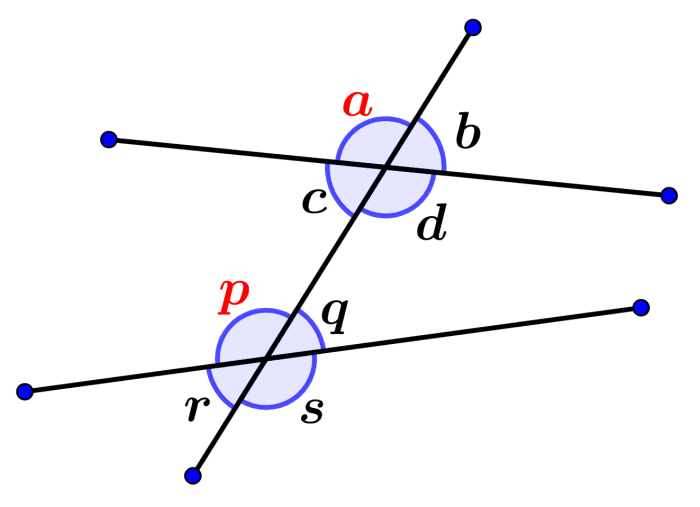
Por ejemplo, en la siguiente figura, los ángulos a y p son correspondientes.
La transversal puede intersecar tanto a dos líneas paralelas como a dos líneas no-paralelas. Entonces, los ángulos correspondientes pueden ser de dos tipos:
- Ángulos correspondientes formados por líneas paralelas y una transversal
- Ángulos correspondientes formados por líneas no-paralelas y una transversal
A continuación, aprenderemos sobre estos dos tipos de ángulos correspondientes.
Ángulos correspondientes entre paralelas y transversales
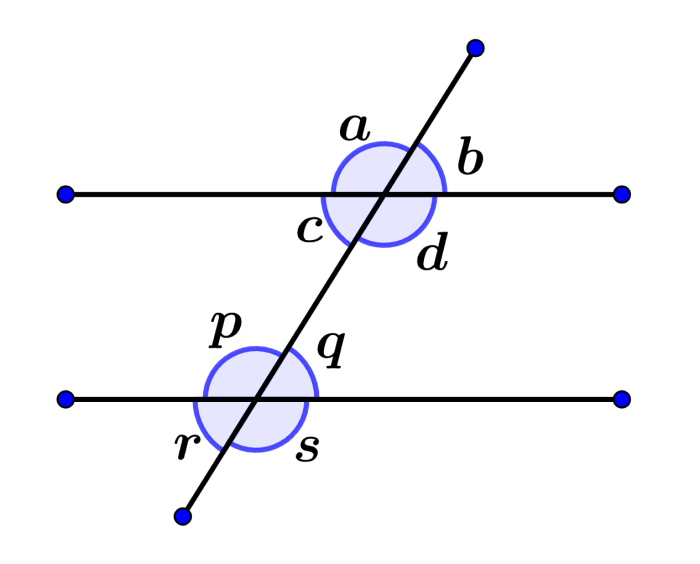
Si es que una línea transversal cruza a dos líneas paralelas, entonces, los ángulos correspondientes formados tienen la misma medida. En el siguiente diagrama, podemos ver que las dos líneas paralelas son intersecadas por una transversal, lo cual forma ocho ángulos con la transversal.
Entonces, los ángulos formados por la primera línea con la transversal tienen los mismos ángulos correspondientes formados por la segunda línea con la transversal.
Todos los pares de ángulos correspondientes en la figura son:
- ∠a y ∠p
- ∠c y ∠q
- ∠c y ∠r
- ∠d y ∠s
Sabemos que los ángulos correspondientes formados por dos líneas paralelas siempre son iguales. Entonces, tenemos:
- ∠a = ∠p
- ∠c = ∠q
- ∠c = ∠r
- ∠d = ∠s
Ángulos correspondientes formados por líneas no-paralelas y transversales
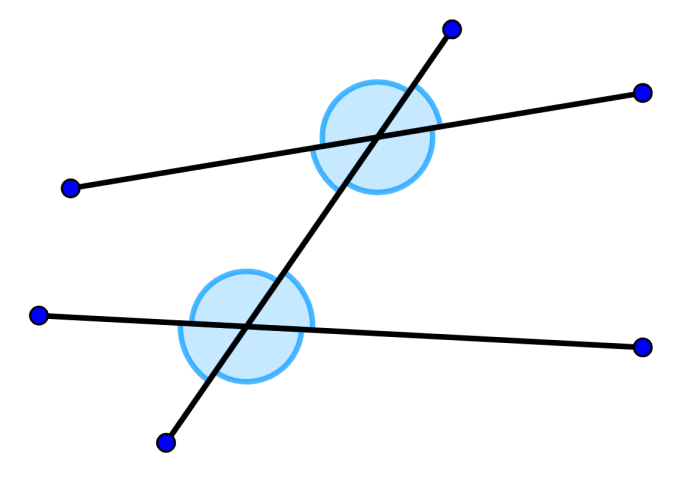
Si es que una línea transversal interseca a dos líneas no paralelas, los ángulos correspondientes formados no tienen ninguna relación el uno con el otro. Estos ángulos no son iguales como en el caso de los ángulos formados por líneas paralelas, pero sí son correspondientes el uno del otro.
De la misma forma, en el caso de una intersección de dos líneas no-paralelas con una línea transversal, no existe una relación entre los ángulos internos, los ángulos externos, los ángulos verticales opuestos y los ángulos consecutivos.
Ejercicios de ángulos correspondientes resueltos
Los siguientes ejercicios muestran cómo pueden ser resueltos los problemas que involucran a ángulos correspondientes. Una técnica muy útil es dibujar un diagrama para encontrar el resto de ángulos fácilmente.
EJERCICIO 1
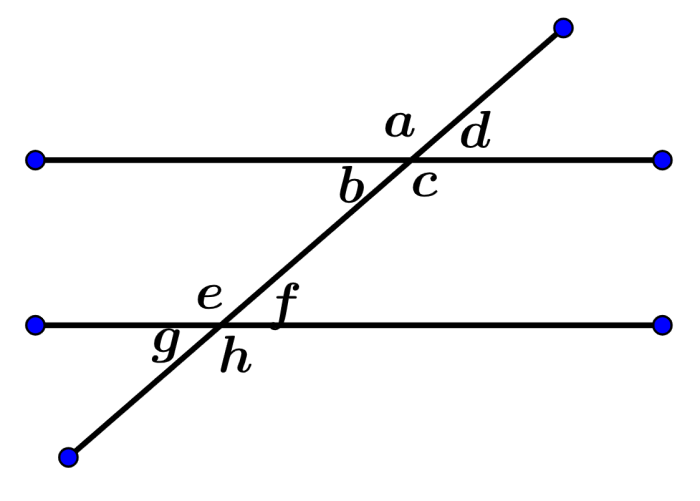
Si es que tenemos que el ángulo d en el siguiente diagrama es igual a 40°, encuentra el resto de ángulos.
Solución: Tenemos el ángulo ∠d = 40°. Sabemos que los ángulos opuestos verticales son iguales, por lo que tenemos:
∠d = ∠b
⇒ ∠b = 40°
Sabemos que los ángulos correspondientes también son iguales, por lo que tenemos:
∠b = ∠ g= 40°
y también
∠d = ∠ f= 40°
Usando los ángulos suplementarios, tenemos:
∠ b + ∠ a = 180°
∠a+ 40° = 180°
∠ a = 140°
Nuevamente, usando ángulos correspondientes, tenemos:
∠ a = ∠ e = 140°
y también
∠d = ∠h = 40°
EJERCICIO 2
Los dos ángulos correspondientes de una figura formada por líneas paralelas miden 8x+10 y 58. Encuentra el valor de x
Solución: Sabemos que los ángulos correspondientes formados por líneas paralelas siempre son congruentes, por lo que tenemos:
8x + 10 = 58
8x = 58 – 10
8x = 48
x = 6
EJERCICIO 3
Los dos ángulos correspondientes de una figura formada por líneas paralelas miden 7y – 12 y 5y + 6. Encuentra la magnitud de un ángulo correspondiente.
Solución: Primero, tenemos que encontrar el valor de y. Sabemos que los dos ángulos correspondientes miden lo mismo, por lo que tenemos:
7y – 12 = 5y + 6
7y – 5y = 6 + 12
2y = 18
y = 9
Ahora, tenemos que sustituir este valor en uno de los ángulos:
7y – 12 = 7(9) -12 = 51
Véase también
¿Interesado en aprender más sobre ángulos? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
