La amplitud de una función es definida como la distancia entre el eje central hasta el valor máximo o valor mínimo de la función. En el caso de las funciones seno y coseno, el eje central es llamado el eje sinusoidal. La amplitud también puede ser definida como la mitad de la distancia entre el valor máximo y el valor mínimo de la función.
A continuación, aprenderemos cómo determinar la amplitud de funciones trigonométricas, especialmente funciones seno y coseno, y resolveremos algunos ejercicios de práctica.
TRIGONOMETRÍA
Relevante para…
Aprender a encontrar la amplitud de funciones trigonométricas.
TRIGONOMETRÍA
Relevante para…
Aprender a encontrar la amplitud de funciones trigonométricas.
¿Cuál es la amplitud de funciones coseno?
Podemos determinar la amplitud de funciones coseno al comparar a la función con su forma general. La forma general de una función coseno es:
$latex f(x)=\pm A~\cos(B(x+C))+D$
En la forma general, el coeficiente A es la amplitud del coseno. Si es que no hay ningún número en frente del coseno, sabemos que la amplitud es 1. La amplitud puede ser entendida de mejor manera usando la gráfica de una función coseno.
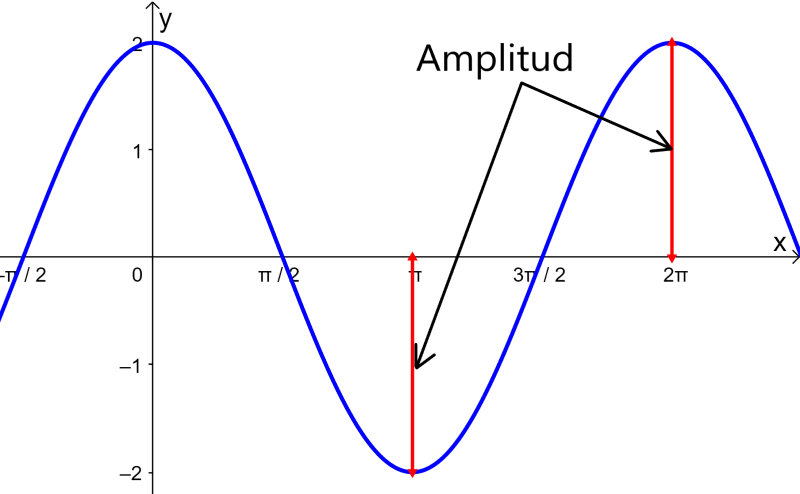
La siguiente representa a la gráfica de la función $latex y=2~\cos(x)$. La amplitud de esta función es 2.
La amplitud es medida como una distancia, por lo que usamos el valor absoluto del valor máximo o valor mínimo de la función. Por ejemplo, en el caso de la función $latex y=-2~\cos(x)$, la gráfica tendría una reflexión con respecto al eje x. Sin embargo, esta función seguiría teniendo la misma amplitud.
En esta función, el eje sinusoidal se ubica en el eje x. El eje sinusoidal se ubica exactamente en la mitad entre los picos y los hoyos de la función. Si es que la función fuera trasladada verticalmente, el eje sinusoidal sería trasladado por la misma cantidad manteniendo su posición inicial con respecto a los picos y hoyos de la función.
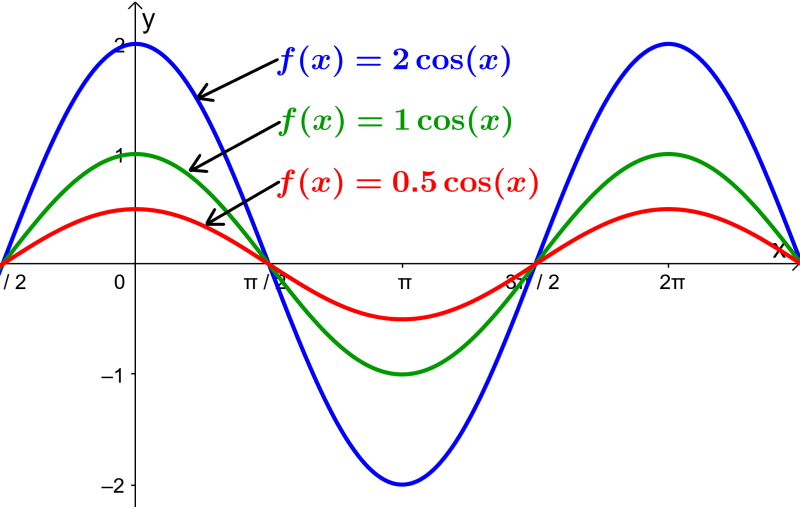
Conociendo el valor de la amplitud de la función, es posible determinar cómo se verá la gráfica de la función. A medida que la amplitud de la función se hace más grande, su gráfica se ve más alta. De igual forma, a medida que la amplitud de la función se hace más pequeña, su gráfica se ve más baja.
¿Cuál es la amplitud de funciones seno?
La forma general de una función seno es:
$latex f(x)=\pm A~\sin(B(x+C))+D$
En esta forma, el coeficiente A es la amplitud del seno. Si es que no tenemos a ningún número presente, entonces, es asumido que la amplitud es 1. Podemos definir a la amplitud usando una gráfica. La siguiente es la gráfica de la función $latex y=2~\sin(x)$, la cual tiene una amplitud de 2:
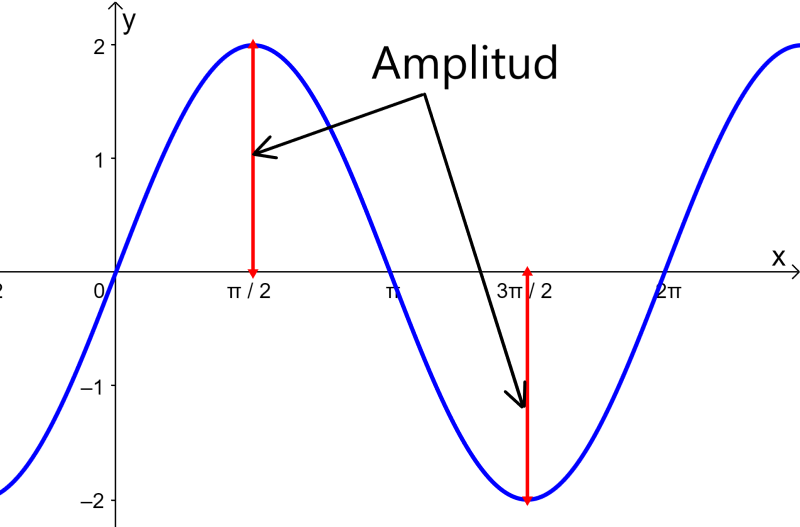
Observamos que la amplitud es 2 en vez de 4. En este caso, la amplitud corresponde al valor absoluto del valor máximo o valor mínimo de la función. Si es que tuviéramos la función $latex y=-2~\sin(x)$, la gráfica estaría reflejada con respecto al eje x, pero su amplitud seguiría siendo la misma.
El eje sinusoidal es la línea horizontal que se ubica entre los picos y los hoyos. En esta función, el eje sinusoidal es simplemente el eje x. Sin embargo, si es que la gráfica fuera trasladada verticalmente, el eje sinusoidal ya no estaría en el eje x, sino que se ubicaría exactamente en la mitad de los picos y los hoyos.
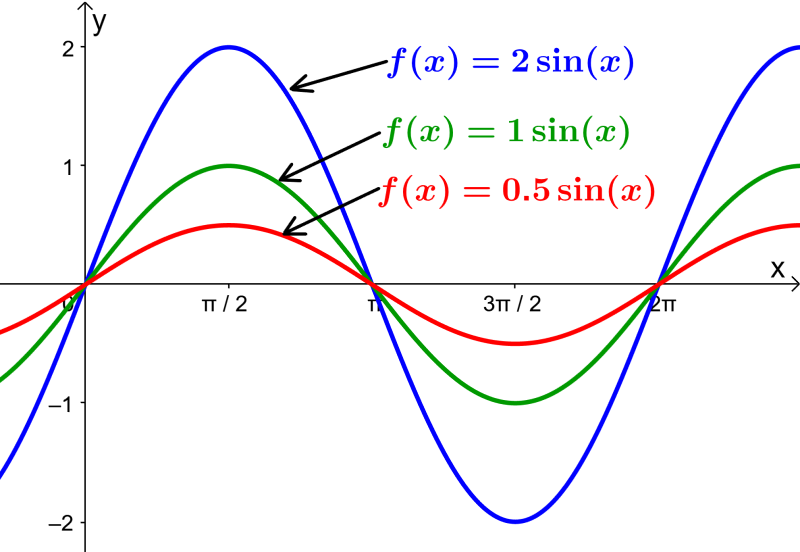
Entre más grande es la amplitud de la función, más alta se verá su gráfica. Por otra parte, entre menor sea la amplitud de la función, más baja se verá su gráfica.
Ejercicios de amplitud de funciones trigonométricas resueltos
EJERCICIO 1
Si es que tenemos la función $latex y=4~\cos(2x)$, ¿cuál es su amplitud?
Solución
Usamos la forma general $latex y=A~\cos(B(x+C))+D$ y encontramos el valor de A para determinar la amplitud. Si es que comparamos a la forma general con la función dada, tenemos:
$latex A=4$
Esto significa que la amplitud es igual a 4.
EJERCICIO 2
¿Cuál es la amplitud de la función $latex y=3~\sin(2x)$?
Solución
Para determinar la amplitud de la función, tenemos que compararla con la forma general $latex y=A~\sin(B(x+C))+D$. Comparando las funciones, vemos que tenemos:
$latex A=3$
Esto significa que la amplitud es igual a 3.
EJERCICIO 3
¿Cuál es la amplitud de la función coseno $latex y=-11~\cos(3x)+4$?
Solución
Comparamos a esta función con la forma general $latex y=A~\cos(B(x+C))+D$. Al hacer esto, podemos encontrar el siguiente valor:
$latex A=-11$
Sabemos que la amplitud es medida usando el valor absoluto, por lo que la amplitud es igual a 11.
EJERCICIO 4
Si es que tenemos la función seno $latex y=-4~\sin(4x)+1$, ¿cuál es su amplitud?
Solución
Usamos la forma general $latex y=A~\sin(B(x+C))+D$ y la comparamos con la función dada. Al compararlas, vemos que tenemos:
$latex A=-4$
Sabemos que la amplitud es el valor absoluto de este parámetro, por lo que la amplitud es igual a 4.
EJERCICIO 5
Si es que tenemos a la función $latex y=\frac{1}{3}\cos(-\frac{1}{2}x-3)$, ¿cuál es su amplitud?
Solución
Nuevamente, comparamos a la función dada con la forma general $latex y=A~\cos(B(x+C))+D$. Entonces, tenemos el valor:
$latex A=\frac{1}{3}$
La amplitud es igual a $latex \frac{1}{3}$. Podemos ver que la amplitud también puede ser un número fraccionario y menor que 1.
EJERCICIO 6
¿Cuál es la amplitud de la función $latex y=\frac{1}{3}\sin(-\frac{1}{4}x-4)$?
Solución
Nuevamente, tenemos que comparar la función dada con la forma general $latex y=A~\sin(B(x+C))+D$. Al realizar esto, tenemos:
$latex A=\frac{1}{3}$
La amplitud es igual a $latex \frac{1}{3}$. Entonces, la amplitud no tiene que ser necesariamente un valor entero.
EJERCICIO 7
¿Cuál es la amplitud de la función $latex y=3\cos(\frac{2}{3}(5x-2))$?
Solución
Esta función tiene a un factor que está en frente. Toda la función está siendo multiplicada por el 3. Comparando a esta función con la forma general $latex y=A~\cos(B(x+C))+D$, tenemos:
$latex A=3(\frac{2}{3})$
$latex A=2$
La amplitud de la función es 2.
EJERCICIO 8
Si es que tenemos la función $latex y=2(\frac{3}{2}\sin(2x-2))$, ¿cuál es su amplitud?
Solución
En este caso, vemos que toda la función está siendo multiplicada por el 2. Esto significa que cuando comparamos a la función con la forma general $latex y=A~\sin(B(x+C))+D$, tenemos:
$latex A=2(\frac{3}{2})$
$latex A=3$
La amplitud de la función es 3.
Ejercicios de amplitud de funciones trigonométricas para resolver
¿Cuál es la amplitud de la función $latex y=2.1(-2\cos(\frac{1}{2}x)-5)$?
Escribe la respuesta en la casilla.
Véase también
¿Interesado en aprender más sobre funciones trigonométricas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
