El periodo de la función seno es 2π. Esto significa que el valor de la función es el mismo cada 2π unidades. Similar a otras funciones trigonométricas, la función seno es una función periódica, lo que significa que se repite en intervalos regulares. El intervalo de la función seno es 2π.
Por ejemplo, tenemos sin(π)=0. Si es que sumamos 2π a la entrada de la función, tenemos sin(π+2π), lo cual es igual a sin(3π). Debido a que tenemos sin(π)=0, también tenemos sin(3π)=0. Cada vez que sumemos 2π de los valores de la entrada, obtendremos el mismo resultado.
Periodo de la función seno básica
La función seno básica es $latex y=\sin(x)$. Dado que esta función puede ser evaluada para cualquier número real, la función seno está definida para todos los números reales. El periodo de esta función puede ser observado claramente en su gráfica, ya que es la distancia entre puntos «equivalentes».
Dado que la gráfica de $latex y=\sin(x)$ se ve como un único patrón que se repite una y otra vez, podemos pensar en el periodo como la distancia en el eje x antes de que la gráfica empiece a repetirse.
Observando a la gráfica, vemos que la gráfica se repite después de 2π. Esto significa que la función es periódica con un periodo de 2π. En el círculo unitario, 2π equivale a una vuelta completa alrededor del círculo.
Cualquier cantidad mayor que 2π significa que estamos repitiendo la vuelta. Esta es la razón por la que el valor de la función es el mismo cada 2π.
Cambiar el periodo de la función seno
El periodo de la función seno básica $latex y=\sin(x)$ es 2π, pero si es que x es multiplicada por una constante, el periodo de la función puede cambiar.
Si es que x es multiplicada por un número mayor que 1, eso «acelera» a la función y el periodo será más pequeño. Eso significa que no tomará mucho para que la función empiece a repetirse. Por ejemplo, si es que tenemos la función $latex y=\sin(2x)$, esto hace que la «velocidad» de la función original se duplique. En este caso, el periodo es π.
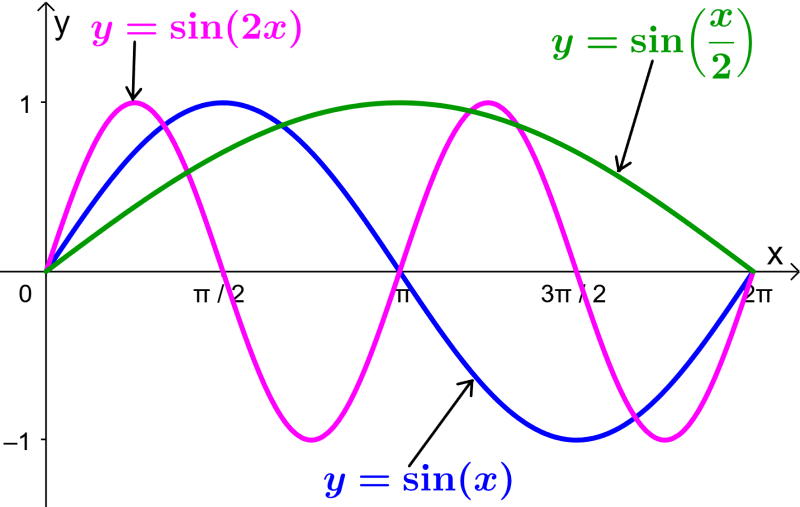
Por otra parte, si es que x es multiplicada por un número entre el 0 y el 1, esto hace que la función reduzca su «velocidad» y el periodo será más grande, ya que tomará más tiempo para que la función se repita.
Por ejemplo, la función $latex y=\sin(\frac{x}{2})$ reduce a la mitad la «velocidad» de la función original. El periodo de esta función es 4π.
Encontrar el periodo de una función seno
Para encontrar el periodo de una función seno, debemos considerar al coeficiente de la x que está dentro de la función. Podemos usar la B para representar a este coeficiente. Entonces, si es que tenemos una ecuación en la forma $latex y=\sin(Bx)$, tenemos la siguiente fórmula:
| $latex \text{Periodo}=\frac{2\pi}{|B|}$ |
En el denominador, tenemos |B|. Esto significa que tomamos el valor absoluto de B. Entonces, si es que B es un número negativo, simplemente tomamos la versión positiva del número.
Esta fórmula funciona incluso si es que tenemos variaciones más complejas de la función seno como $latex y=3\sin(2x+4)$. Solo el coeficiente de x importa al momento de calcular el periodo, por lo que tendríamos:
$latex \text{Periodo}=\frac{2\pi}{|B|}$
$latex \text{Periodo}=\frac{2\pi}{2}$
$latex \text{Periodo}=\pi$
Ejercicios de periodo de funciones seno resueltos
Lo aprendido sobre el periodo de funciones seno es usado para resolver los siguientes ejercicios. Intenta resolver los ejercicios tú mismo antes de mirar la respuesta.
EJERCICIO 1
¿Cuál es el periodo de la función $latex y=\sin(3x)$?
Solución
Usamos la fórmula del periodo con el valor $latex |B|=3$. Entonces, tenemos:
$latex \text{Periodo}=\frac{2\pi}{|B|}$
$latex \text{Periodo}=\frac{2\pi}{3}$
El periodo de la función es $latex \frac{2}{3}\pi$.
EJERCICIO 2
Tenemos la función seno $latex y=3\sin(4x)+1$. ¿Cuál es su periodo?
Solución
El único valor que necesitamos es el coeficiente de x. Entonces, usamos el valor $latex |B|=4$ en la fórmula del periodo:
$latex \text{Periodo}=\frac{2\pi}{|B|}$
$latex \text{Periodo}=\frac{2\pi}{4}$
$latex \text{Periodo}=\frac{\pi}{2}$
El periodo de la función es $latex \frac{\pi}{2}$.
EJERCICIO 3
¿Cuál es el periodo de la función $latex y=\frac{1}{2}\sin(-\frac{1}{4}x-4)$?
Solución
Sólo tenemos que usar al coeficiente de x para encontrar al periodo. Vemos que en este caso, el coeficiente es negativo, por lo que tomamos su versión positiva.
Entonces, usamos el valor $latex |B|=\frac{1}{4}$ en la fórmula del periodo:
$latex \text{Periodo}=\frac{2\pi}{|B|}$
$latex \text{Periodo}=\frac{2\pi}{\frac{1}{4}}$
$latex \text{Periodo}=8\pi$
El periodo de la función es $latex 8\pi$.
Ejercicios de periodo de funciones seno para resolver
Resuelve los siguientes ejercicios de práctica usando lo aprendido sobre el periodo de funciones seno. Si necesitas ayuda con esto, puedes mirar los ejercicios resueltos de arriba.
Véase también
¿Interesado en aprender más sobre senos Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
