El coseno de un ángulo es encontrado al relacionar a los lados de un triángulo rectángulo. El coseno es igual a la longitud del lado adyacente al ángulo dividido por la longitud de la hipotenusa. El coseno también es igual al seno del ángulo complementario. Los valores del coseno de los ángulos más importantes pueden ser obtenidos usando las proporciones de los triángulos conocidos.
A continuación, conoceremos sobre el coseno de ángulos más a detalle y resolveremos algunos ejercicios de práctica.
TRIGONOMETRÍA
Relevante para…
Aprender sobre el coseno de un ángulo con ejercicios.
TRIGONOMETRÍA
Relevante para…
Aprender sobre el coseno de un ángulo con ejercicios.
Definición del coseno de un ángulo
El coseno de un ángulo de un triángulo rectángulo es definido como la longitud del lado adyacente al ángulo dividida por la longitud de la hipotenusa del triángulo.
Adicionalmente, el coseno de un ángulo es definido como el seno del ángulo complementario. El ángulo complementario es igual al ángulo dado restado de 90° (un ángulo recto). Por ejemplo, si tenemos al ángulo 40°, su complemento es 50°. Entonces, para cualquier ángulo θ, tenemos:
$latex \cos (\theta)=\sin (90^{\circ}-\theta)$
En términos de radianes, tenemos:
$latex \cos (\theta)=\sin (\frac{\pi}{2}-\theta)$
Triángulos rectángulos y cosenos
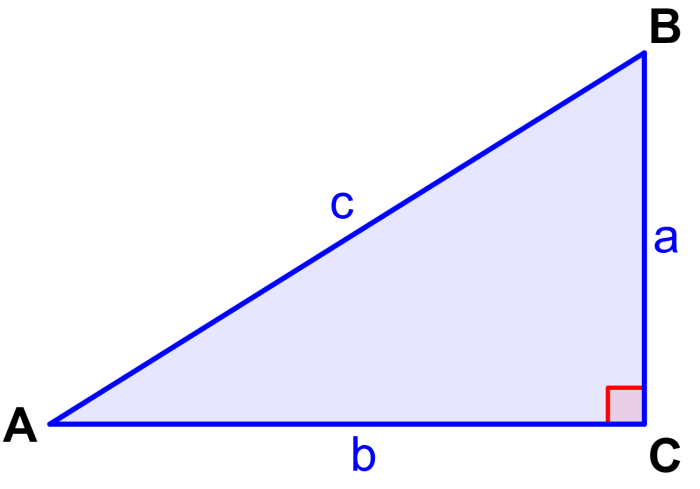
Observemos al triángulo rectángulo ABC que tiene un ángulo recto en C.
Generalmente, usamos a la letra a para denotar al lado que está opuesto al ángulo A, usamos a la letra b para denotar al lado que está opuesto al ángulo B y usamos a la letra c para denotar al lado que está opuesto al ángulo C.
Dado que la suma de los ángulos internos de un triángulo es igual a 180° y el ángulo C mide 90°, sabemos que los ángulos A y B son complementarios, es decir, suman 90°.
Esto significa que el coseno de B es igual al seno de A. El coseno de un ángulo en un triángulo rectángulo es igual al lado adyacente dividido por la hipotenusa:
| $latex \cos=\frac{\text{adyacente}}{\text{hipotenusa}}$ |
En el triángulo de arriba, tenemos $latex \cos(A)=\frac{b}{c}$ y también $latex \cos(B)=\frac{a}{c}$.
Cosenos para ángulos especiales comunes
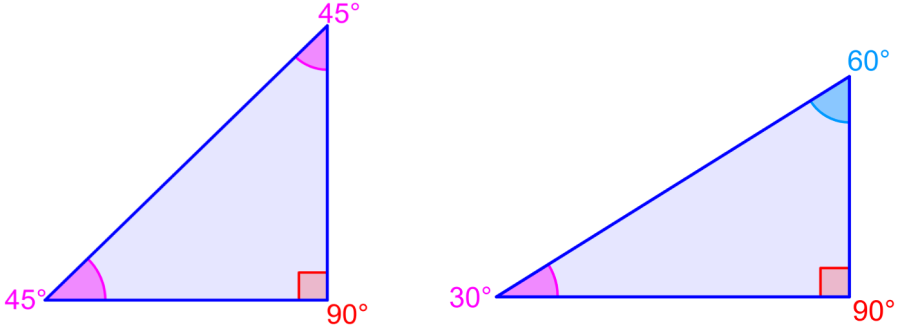
Podemos obtener el resultado de cosenos de ángulos especiales basándonos en las proporciones de los lados. Por ejemplo, el ángulo de 45° es encontrado en un triángulo isósceles rectángulo, el cual tiene los ángulos 45°-45°-90°.
Sabemos que los triángulos rectángulos tienen la relación $latex {{c}^2}={{a}^2}+{{b}^2}$, pero en este caso, $latex a=b$, por lo que tenemos $latex {{c}^2}=2{{a}^2}$. Esto significa que tenemos $latex c=a\sqrt{2}$.
Entonces, tanto el seno como el coseno de 45° son iguales a $latex \frac{1}{\sqrt{2}}$, lo cual puede ser escrito como $latex \frac{\sqrt{2}}{2}$.
En el caso del triángulo rectángulo con ángulos 30°-60°-90°, las proporciones de sus lados son 1:$latex \sqrt{3}$:2. Usando estas proporciones, tenemos $latex \sin(30^{\circ})=\cos(60^{\circ})=\frac{1}{2}$ y también tenemos $latex \sin(60^{\circ})=\cos(30^{\circ})=\frac{\sqrt{3}}{2}$.
| Grados | Radianes | Coseno |
| 90° | $latex \frac{\pi}{2}$ | 0 |
| 60° | $latex \frac{\pi}{3}$ | $latex \frac{1}{2}$ |
| 45° | $latex \frac{\pi}{4}$ | $latex \frac{\sqrt{2}}{2}$ |
| 30° | $latex \frac{\pi}{6}$ | $latex \frac{\sqrt{3}}{2}$ |
| 0° | 0 | 1 |
Ejercicios de coseno de un ángulo resueltos
Los siguientes ejercicios pueden ser usados para seguir el proceso usado para resolver problemas relacionados con cosenos. Estos y los siguientes ejercicios hacen referencia al triángulo rectángulo usado arriba.
EJERCICIO 1
Si es que tenemos que $latex \cos(A)=0.2$ y $latex b=3$, ¿cuál es el valor de c?
Solución
Haciendo referencia al triángulo rectángulo que tenemos arriba, vemos que tenemos $latex \cos(A)=\frac{b}{c}$. Podemos usar los valores dados en esta ecuación y resolver para c:
$latex \cos(A)=\frac{b}{c}$
$latex 0.2=\frac{3}{c}$
$latex c=\frac{3}{0.2}$
$latex c=15$
El valor de la hipotenusa es 15.
EJERCICIO 2
Si es que tenemos $latex a=10$ y $latex \cos(B)=\frac{1}{3}$, encuentra el valor de c.
Solución
Del triángulo rectángulo de arriba, podemos deducir que tenemos $latex \cos(B)=\frac{a}{c}$. Usando los valores dados en la fórmula y resolviendo para c, tenemos:
$latex \cos(B)=\frac{a}{c}$
$latex \frac{1}{3}=\frac{10}{c}$
$latex c=3(10)$
$latex c=30$
El valor de la hipotenusa es 30.
EJERCICIO 3
¿Cuál es el valor de A si es que tenemos $latex b=5$ y $latex c=8$?
Solución
Podemos formar la siguiente relación $latex \cos(A)=\frac{b}{c}$. Entonces, usando los valores dados, tenemos:
$latex \cos(A)=\frac{b}{c}$
$latex \cos(A)=\frac{5}{8}$
$latex \cos(A)=0.625$
Ahora usamos la función $latex {{\cos}^{-1}}$ en una calculadora para obtener el resultado:
$latex {{\cos(0.625)}^{-1}}=51.3$°
El águlo A mide 51.3°.
→ Calculadora de Coseno (Grados y Radianes)
Ejercicios de coseno de un ángulo para resolver
Practica lo aprendido sobre el coseno de un ángulo para resolver los siguientes ejercicios de práctica. Si necesitas ayuda con esto, puedes mirar los ejercicios de práctica de arriba.
Véase también
¿Interesado en aprender más sobre cosenos? Mira estas páginas: