Los sistemas de ecuaciones 2×2 son sistemas con dos ecuaciones y dos incógnitas. Existen varios métodos distintos para resolver estos sistemas de ecuaciones. En este caso, nos enfocaremos en dos métodos, en el método de eliminación y el método de sustitución.
Empezaremos explorando un breve resumen sobre cómo resolver sistemas de ecuaciones 2×2 para luego mirar varios ejercicios resueltos.
ÁLGEBRA
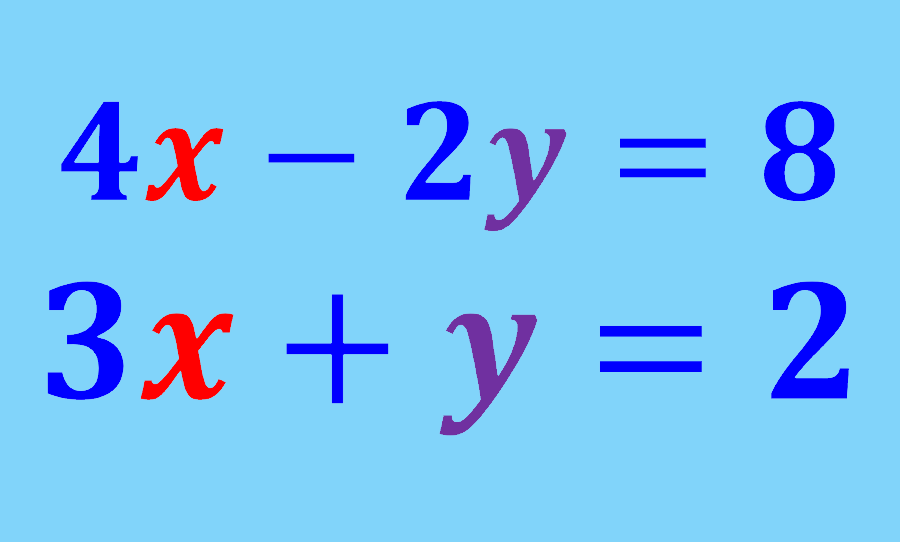
Relevante para…
Practicar la resolución de ejercicios sistemas de ecuaciones 2×2.
ÁLGEBRA
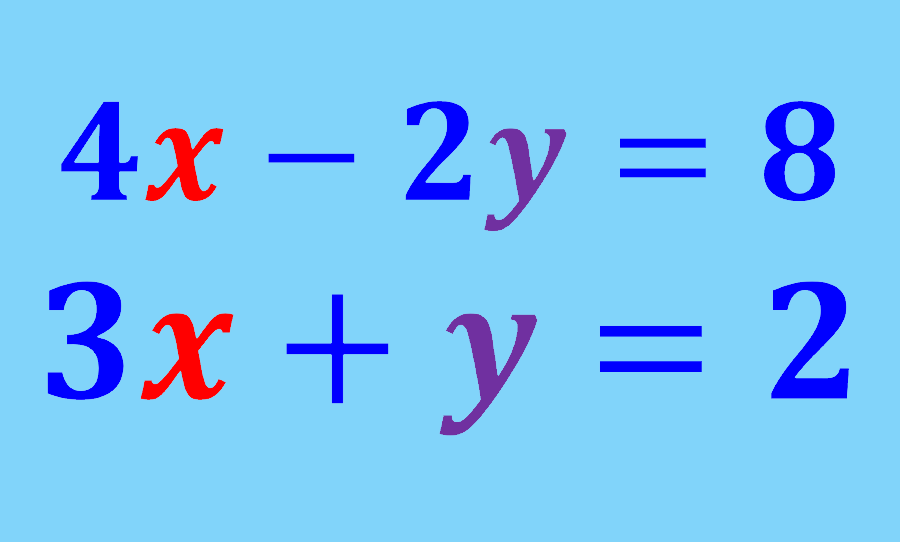
Relevante para…
Practicar la resolución de ejercicios sistemas de ecuaciones 2×2.
Resumen de sistemas de ecuaciones 2×2
Podemos resolver sistemas de ecuaciones 2×2 con tres métodos principales, con el método de eliminación, el método de sustitución y el método gráfico. Aquí nos enfocaremos en el método de eliminación y el método de sustitución.
Resolver sistemas de ecuaciones 2×2 con el método de sustitución
Podemos seguir los siguientes pasos para resolver el sistema por sustitución:
Paso 1: Simplificar las ecuaciones: Esto incluye eliminar paréntesis, combinar términos semejantes y eliminar fracciones.
Paso 2: Resolver cualquier ecuación para una variable. No importa la ecuación o la variable que escojamos.
Paso 3: Sustituye la expresión obtenida en el paso 2 en la otra ecuación. Esto resultará en una sola ecuación con una variable.
Paso 4: Resuelve la ecuación obtenida en el paso 3.
Paso 5: Sustituye el valor del paso 4 en cualquiera de las otras ecuaciones y resuelve para la otra incógnita.
Resolver sistemas de ecuaciones 2×2 por el método de eliminación
Usamos los siguientes pasos para resolver el sistema de ecuaciones por eliminación:
Paso 1: Simplificar las ecuaciones y colocarlas en la forma Ax+By=C.
Paso 2: Multiplica una o ambas ecuaciones por algún número de modo que obtengamos coeficientes opuestos o bien para x o para y. Necesitamos eliminar una de las variables al sumar las ecuaciones. Entonces, tenemos que lograr que un coeficiente sea a y el otro –a.
Paso 3: Suma las ecuaciones. Al hacer esto eliminaremos una variable y tendremos una ecuación con una incógnita.
Paso 4: Resuelve la ecuación del paso 3 para la variable restante.
Paso 5: Sustituye el valor del paso 4 en cualquier ecuación y resuelve para la segunda variable.
10 Ejercicios de sistemas de ecuaciones 2×2 resueltos
EJERCICIO 1
Resuelve el sistema de ecuaciones usando el método de sustitución: $latex \begin{cases}x+2y=10 \\ 2x-y=5 \end{cases}$
Solución
Paso 1: No tenemos nada para simplificar.
Paso 2: Podemos resolver la primera ecuación para x:
$latex x+2y=10$
$latex x=10-2y$
Paso 3: Sustituimos la expresión $latex x=10-2y$ en la segunda ecuación:
$latex 2x-y=5$
$latex 2(10-2y)-y=5$
$latex 20-4y-y=5$
Paso 4: Resuelve para y:
$latex 20-4y-y=5$
$latex -5y=-15$
$latex y=3$
Paso 5: Sustituimos $latex y=3$ en la primera ecuación:
$latex x+2y=10$
$latex x+2(3)=10$
$latex x=4$
EJERCICIO 2
Resuelve el sistema de ecuaciones usando el método de eliminación: $latex \begin{cases}x-y=3 \\ 2x+y=12 \end{cases}$
Solución
Paso 1: No tenemos nada que simplificar y ambas ecuaciones ya están en la forma Ax+By=C.
Paso 2: Ya tenemos coeficientes opuestos en la variable y.
Paso 3: Sumamos las ecuaciones:
$latex x-y=3$
$latex + \hspace{1cm} 2x+y=12$
___________________
$latex 3x=15$
Paso 4: Resolvemos para x:
$latex 3x=15$
$latex x=5$
Paso 5: Sustituimos $latex x=5$ en la segunda ecuación:
$latex 2x+y=12$
$latex 2(5)+y=12$
$latex 10+y=12$
$latex y=2$
EJERCICIO 3
Resuelve lo siguiente usando el método de sustitución: $latex \begin{cases}-2x-y=1 \\ 3x+4y=6 \end{cases}$
Solución
Paso 1: No tenemos nada para simplificar.
Paso 2: Resolvemos la primera ecuación para y:
$latex -2x-y=1$
$latex -y=1+2x$
$latex y=-1-2x$
Paso 3: Sustituimos la expresión $latex y=-1-2x$ en la segunda ecuación:
$latex 3x+4y=6$
$latex 3x+4(-1-2x)=6$
$latex 3x-4-8x=6$
Paso 4: Resuelve para x:
$latex 3x-4-8x=6$
$latex -5x=10$
$latex x=-2$
Paso 5: Sustituimos $latex x=-2$ en la primera ecuación:
$latex -2x-y=1$
$latex -2(-2)-y=1$
$latex 4-y=1$
$latex -y=-3$
$latex y=3$
EJERCICIO 4
Resuelve el sistema de ecuaciones usando el método de eliminación: $latex \begin{cases}y=2x+7 \\ -6x-2y=-4 \end{cases}$
Solución
Paso 1: Escribimos a las ecuaciones en la forma Ax+By=C:
$latex \begin{cases}-2x+y=7 \\ -6x-2y=-4 \end{cases}$
Paso 2: Multiplicamos la primera ecuación por 2 para obtener coeficientes opuestos en y:
$latex \begin{cases}-4x+2y=14 \\ -6x-2y=-4 \end{cases}$
Paso 3: Sumamos las ecuaciones:
$latex -4x+2y=14$
$latex + \hspace{1cm} -6x-2y=-4$
___________________
$latex -10x=10$
Paso 4: Resolvemos para x:
$latex -10x=10$
$latex x=-1$
Paso 5: Sustituimos $latex x=-1$ en la primera ecuación:
$latex y=2x+7$
$latex y=2(-1)+7$
$latex y=5$
EJERCICIO 5
Resuelve el sistema de ecuaciones usando el método de sustitución: $latex \begin{cases}2(2x-4)+y=3 \\ -x+2y=4 \end{cases}$
Solución
Paso 1: Simplificamos la primera ecuación:
$latex \begin{cases}4x-8+y=3 \\ -x+2y=4 \end{cases}$
Paso 2: Resolvemos la primera ecuación para y:
$latex 4x-8+y=3$
$latex y=-4x+11$
Paso 3: Sustituimos la expresión $latex y=-4x+11$ en la segunda ecuación:
$latex -x+2y=4$
$latex -x+2(-4x+11)=4$
$latex -x-8x+22=4$
Paso 4: Resolvemos para x:
$latex -x-8x+22=4$
$latex -9x=-18$
$latex x=2$
Paso 5: Sustituimos $latex x=2$ en la segunda ecuación:
$latex -x+2y=4$
$latex -2+2y=4$
$latex 2y=6$
$latex y=3$
EJERCICIO 6
Resuelve lo siguiente usando el método de eliminación: $latex \begin{cases}2x=3y-14 \\ 2y=x+8 \end{cases}$
Solución
Paso 1: Escribimos a las ecuaciones en la forma Ax+By=C:
$latex \begin{cases}2x-3y=-14 \\ -x+2y=8 \end{cases}$
Paso 2: Multiplicamos la segunda ecuación por 2 para obtener coeficientes opuestos en la x:
$latex \begin{cases}2x-3y=-14 \\ -2x+4y=16 \end{cases}$
Paso 3: Sumamos las ecuaciones:
$latex 2x-3y=-14$
$latex + \hspace{1cm} -2x+4y=16$
___________________
$latex y=2$
Paso 4: Ya obtuvimos el valor de y:
$latex y=2$
Paso 5: Sustituimos $latex y=2$ en la primera ecuación:
$latex 2x=3y-14$
$latex 2x=3(2)-14$
$latex 2x=-8$
$latex x=-4$
EJERCICIO 7
Resuelve el sistema de ecuaciones: $latex \begin{cases}2x-3y=7 \\ 2x+3y=1 \end{cases}$
Solución
Vamos a resolver por sustitución. Entonces, resolviendo la primera ecuación para x, tenemos:
$latex 2x-3y=7$
$latex 2x=3y+7$
$latex x=\frac{3y+7}{2}$
Usando la expresión $latex x=\frac{3y+7}{2}$ en la segunda ecuación, tenemos:
$latex 2x+3y=1$
$latex 2\left(\frac{3y+7}{2}\right)+3y=1$
$latex 3y+7+3y=1$
Resolviendo la ecuación para y, tenemos:
$latex 3y+7+3y=1$
$latex 6y=-6$
$latex y=-1$
Usando el valor y=-1 en la segunda ecuación, tenemos:
$latex 2x+3y=1$
$latex 2x+3(-1)=1$
$latex 2x-3=1$
$latex 2x=4$
$latex x=2$
La solución al sistema es $latex x=2,~~y=-1$.
EJERCICIO 8
Resuelve el sistema de ecuaciones: $latex \begin{cases}2x-7y=1 \\ 2x+3y=11 \end{cases}$
Solución
Vamos a resolver por eliminación. Entonces, multiplicamos a la segunda ecuación por -1 para obtener coeficientes opuestos en x:
$latex \begin{cases}2x-7y=1 \\ -2x-3y=-11 \end{cases}$
Al sumar las ecuaciones, tenemos:
$latex 2x-7y=1$
$latex + \hspace{1cm} -2x-3y=-11$
___________________
$latex -10y=-10$
Resolviendo para y, tenemos:
$latex y=1$
Usando el valor y=1 en la primera ecuación, tenemos:
$latex 2x-7y=1$
$latex 2x-7(1)=1$
$latex 2x=8$
$latex x=4$
La solución es $latex x=4,~~y=1$.
EJERCICIO 9
Resuelve el sistema de ecuaciones: $latex \begin{cases}3x-4y=5 \\ 6x-4y=2 \end{cases}$
Solución
Podemos empezar simplificando la segunda ecuación al dividirla por 2:
$latex \begin{cases}3x-4y=5 \\ 3x-2y=1 \end{cases}$
Ahora, vamos a resolver por sustitución. Entonces, resolvemos la segunda ecuación para x y tenemos:
$latex 3x-2y=1$
$latex 3x=2y+1$
$latex x=\frac{2y+1}{3}$
Usando $latex x=\frac{2y+1}{3}$ en la primera ecuación, tenemos:
$latex 3x-4y=5$
$latex 3\left(\frac{2y+1}{3}\right)-4y=5$
$latex 2y+1-4y=5$
Resolviendo la ecuación para y, tenemos:
$latex 2y+1-4y=5$
$latex -2y=4$
$latex y=-2$
Usando el valor y=-2 en la segunda ecuación, tenemos:
$latex 3x-2y=1$
$latex 3x-2(-2)=1$
$latex 3x+4=1$
$latex 3x=-3$
$latex x=-1$
La solución al sistema es $latex x=-1,~~y=-2$.
EJERCICIO 10
Encuentra la solución al sistema de ecuaciones: $latex \begin{cases}3x-y=1 \\ 5x+y=7 \end{cases}$
Solución
Vamos a resolver por eliminación, ya que tenemos coeficientes opuestos en y:
$latex \begin{cases}3x-y=1 \\ 5x+y=7 \end{cases}$
Al sumar las ecuación, tenemos:
$latex 3x-y=1$
$latex + \hspace{1cm} 5x+y=7$
___________________
$latex 8x=8$
Resolviendo la ecuación para x, tenemos:
$latex x=1$
Usando el valor x=1 en la segunda ecuación, tenemos:
$latex 5x+y=7$
$latex 5(1)+y=7$
$latex y=2$
La solución es $latex x=1,~~y=2$.
Ejercicios de sistemas de ecuaciones 2×2 para resolver


Resuelve el sistema de ecuaciones $latex \begin{cases} -2x+3y=7 \\ 3x-y=7 \end{cases} $
Escribe la respuesta en la forma x=?, y=?.
Véase también
¿Interesado en aprender más sobre ecuaciones algebraicas? Mira estas páginas:


