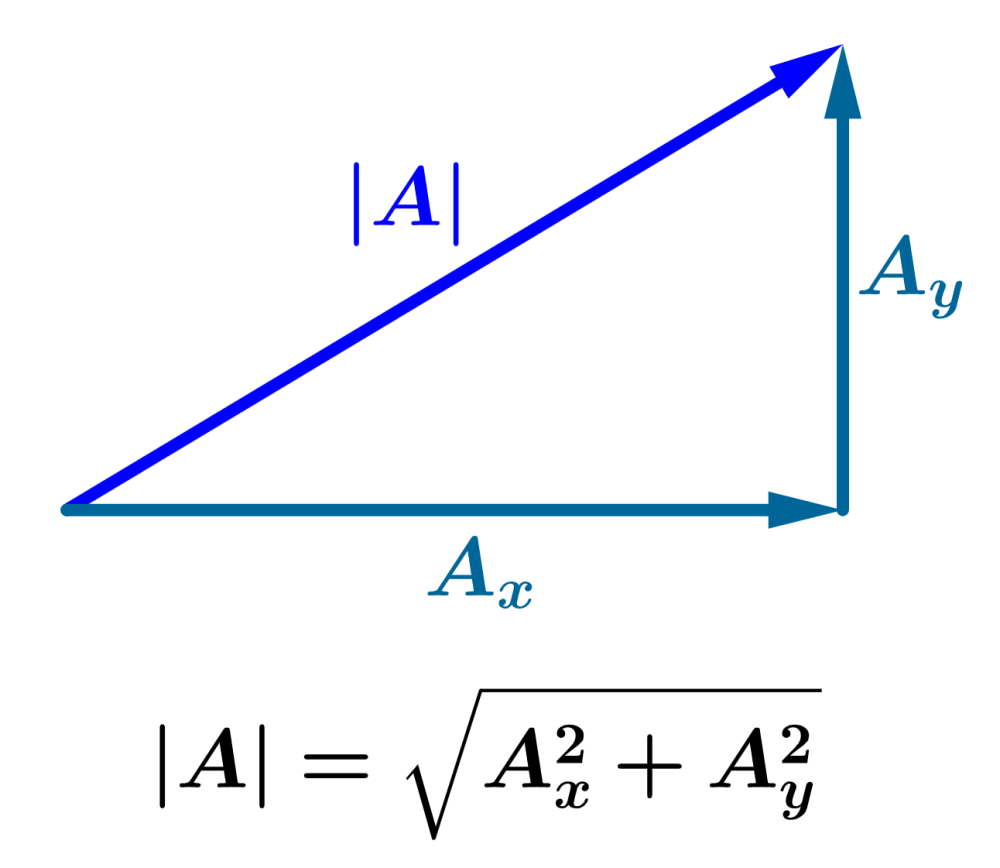El cálculo de magnitudes de vectores nos ayuda a cuantificar el tamaño o la longitud de un vector en el espacio. Para encontrar la magnitud de un vector 2D o 3D, tenemos que usar el teorema de Pitágoras con los componentes correspondientes.
En este artículo, conoceremos las fórmulas para calcular la magnitud de vectores 2D y 3D, proporcionando así una base sólida para seguir explorando los vectores. Veremos varios ejercicios resueltos.
¿Cómo calcular la magnitud de un vector?
Para calcular la magnitud de un vector, podemos usar los componentes del vector en fórmulas estándar que son derivadas a partir del teorema de Pitágoras.
Magnitud de un vector 2D
Consideremos al siguiente vector 2D que tiene los componentes $latex A_{x}$ y $latex A_{y}$.
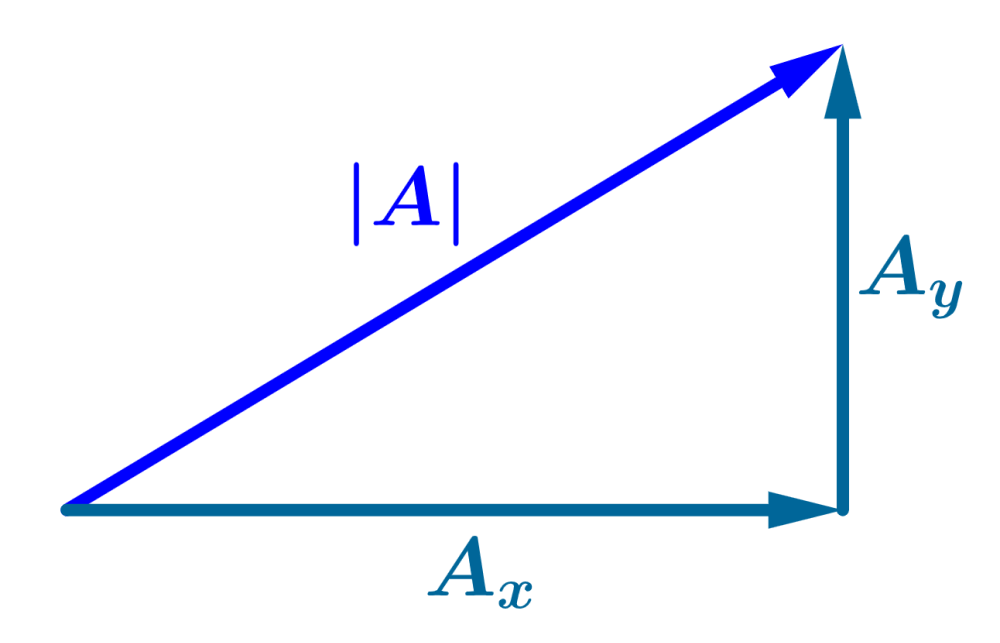
Para encontrar la magnitud de este vector, podemos utilizar el teorema de Pitágoras, que establece que en un triángulo rectángulo, el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de las longitudes de los otros dos lados.
En este caso, la hipotenusa es la magnitud, es decir, $latex |A|$. Los dos lados son $latex A_{x}$ y $latex A_{y}$:
$latex |A|^2=A_{x}^2+A_{y}^2$
Tomando la raíz cuadrada de ambos lados, encontramos la magnitud del vector 2D:
$latex |A| = \sqrt{A_{x}^2+A_{y}^2}$
Magnitud de un vector 3D
Consideremos ahora un vector 3D que tiene los componentes $latex A_{x}$, $latex A_{y}$ y $latex A_{z}$.
Podemos utilizar la misma lógica que para el vector 2D, pero esta vez, utilizamos el teorema de Pitágoras en 3D. Entonces, tenemos:
$latex |A|^2=A_{x}^2+A_{y}^2+A_{z}^2$
Tomando la raíz cuadrada de ambos lados, hallamos la magnitud del vector 3D:
$latex |A| = \sqrt{A_{x}^2+A_{y}^2+A_{z}^2}$
10 Ejercicios resueltos de la magnitud de un vector
EJERCICIO 1
Encuentra la magnitud del vector $latex \vec{A} = 3i+4j$.
Solución
Tenemos los siguientes componentes:
- $latex A_{x}=3$
- $latex A_{y}=4$
Ahora, usamos estos componentes en la fórmula de la magnitud de un vector 2D:
$latex |A| = \sqrt{A_{x}^2+A_{y}^2}$
$latex = \sqrt{3^2 + 4^2} $
$latex = \sqrt{9 + 16}$
$latex = \sqrt{25}$
$latex |A| = 5$
EJERCICIO 2
¿Cuál es la magnitud del vector $latex \vec{B} = -6i+8j$?
Solución
Podemos observar lo siguiente:
- $latex B_{x}=-6$
- $latex B_{y}=8$
Al aplicar la fórmula de la magnitud con los componentes dados, tenemos:
$latex |B| = \sqrt{A_{x}^2+A_{y}^2}$
$latex = \sqrt{(-6)^2 + 8^2} $
$latex = \sqrt{36 + 64}$
$latex = \sqrt{100}$
$latex |B| = 10$
EJERCICIO 3
Determina la magnitud del vector $latex \vec{C} = -5i +12j$.
Solución
Podemos observar lo siguiente:
- $latex C_{x}=-5$
- $latex C_{y}=12$
Usamos la fórmula de la magnitud de un vector 2D:
$latex |C| = \sqrt{C_{x}^2+C_{y}^2}$
$latex = \sqrt{(-5)^2 + 12^2} $
$latex = \sqrt{25 + 144}$
$latex = \sqrt{169}$
$latex |C| = 13$
EJERCICIO 4
Un excursionista comienza en la base de una montaña y camina 6 kilómetros hacia el este y luego 3 kilómetros hacia el norte para llegar a un campamento. ¿Cuál es la distancia en línea recta entre la base y el campamento?
Solución
Podemos representar a la base de la montaña por el origen (0, 0) en un sistema de coordenadas 2D. El movimiento del excursionista puede representarse como un vector 2D, cuyos componentes son la distancia recorrida en dirección este (x) y la distancia recorrida en dirección norte (y).
Entonces, tenemos:
- $latex V_{x}=6$
- $latex V_{y}=3$
Al usar estos componentes en la fórmula de la magnitud, tenemos:
$latex |V| = \sqrt{V_{x}^2+V_{y}^2}$
$latex = \sqrt{6^2 + 3^2} $
$latex = \sqrt{36 + 9}$
$latex = \sqrt{45}$
$latex |V| = 6.71$
La distancia entre la base y el campamento es 6.71 kilómetros.
EJERCICIO 5
Un barco navega 10 kilómetros hacia el oeste y luego 6 kilómetros hacia el sur desde un puerto. ¿Cuál es la distancia más corta entre la posición final del barco y el puerto?
Solución
Representamos al puerto por el origen (0, 0). El movimiento del barco puede representarse como un vector, cuyos componentes son la distancia recorrida en dirección oeste (x) y la distancia recorrida en dirección sur (y).
Como el barco se mueve hacia el oeste ($latex x$ negativo) y hacia el sur ($latex y$ negativo), las componentes del vector son negativos. Entonces,
- $latex V_{x}=-10$
- $latex V_{y}=-6$
Al aplicar la fórmula de la magnitud:
$latex |V| = \sqrt{V_{x}^2+V_{y}^2}$
$latex = \sqrt{(-10)^2 + (-6)^2} $
$latex = \sqrt{100 + 36}$
$latex = \sqrt{136}$
$latex |V| = 11.66$
La distancia más corta entre la posición final del barco y el puerto es de aproximadamente 11.66 kilómetros.
EJERCICIO 6
Encuentra la magnitud del vector $latex \vec{A} = 1i + 2j +2k$.
Solución
Podemos observar lo siguiente:
- $latex A_{x}=1$
- $latex A_{y}=2$
- $latex A_{z}=2$
Al aplicar la fórmula de la magnitud de un vector 3D, tenemos:
$latex |A| = \sqrt{A_{x}^2+A_{y}^2+A_{z}^2}$
$latex = \sqrt{1^2 + 2^2+2^2} $
$latex = \sqrt{1+4+4}$
$latex = \sqrt{9}$
$latex |A| = 3$
EJERCICIO 7
Si es que tenemos el vector $latex \vec{B} = -3i+ 4j+ 2k$, ¿cuál es su magnitud?
Solución
Podemos observar la siguiente información:
- $latex B_{x}=-3$
- $latex B_{y}=4$
- $latex B_{z}=2$
Aplicando la fórmula de la magnitud de un vector 3D, tenemos:
$latex |B| = \sqrt{B_{x}^2+B_{y}^2+B_{z}^2}$
$latex = \sqrt{(-3)^2 + 4^2+2} $
$latex = \sqrt{9 + 16+4}$
$latex = \sqrt{29}$
$latex |B| = 5.385$
EJERCICIO 8
Encuentra la magnitud del vector $latex \vec{C} = 5i -6j+ 8k$.
Solución
Tenemos los siguientes componentes:
- $latex C_{x}=5$
- $latex C_{y}=-6$
- $latex C_{z}=8$
Usando la fórmula de la magnitud, tenemos:
$latex |C| = \sqrt{C_{x}^2+C_{y}^2+C_{z}^2}$
$latex = \sqrt{5^2 + (-6)^2+8^2} $
$latex = \sqrt{25 +36+64}$
$latex = \sqrt{125}$
$latex |C| = 11.18$
EJERCICIO 9
Un dron despega de una ubicación (0, 0, 0) en un sistema de coordenadas 3D. Vuela 30 metros hacia el este, luego 40 metros hacia el norte y finalmente asciende 50 metros en vertical. ¿Cuál es la distancia en línea recta entre las posiciones inicial y final del dron?
Solución
El movimiento del dron puede representarse como un vector 3D, donde los componentes corresponden a las distancias recorridas hacia el este, hacia el norte y hacia arriba:
Entonces, tenemos estos componentes:
- $latex V_{x}=30$
- $latex V_{y}=40$
- $latex V_{z}=50$
Ahora, usamos la fórmula de la magnitud de un vector 3D:
$latex |V| = \sqrt{V_{x}^2+V_{y}^2+V_{z}^2}$
$latex = \sqrt{30^2 + 40^2+50^2} $
$latex = \sqrt{900 + 1600+2500}$
$latex = \sqrt{5000}$
$latex |V| = 70.71$
La distancia en línea recta entre las posiciones inicial y final del dron es de aproximadamente 70.71 metros.
EJERCICIO 10
Un avión vuela a una altitud constante de 5 kilómetros. Vuela 32 kilómetros hacia el sur y 40 kilómetros hacia el oeste. ¿Cuál es la distancia en línea recta entre las posiciones inicial y final del avión?
Solución
El movimiento del avión se puede representar como un vector 3D:
- $latex V_{x}=-40$
- $latex V_{y}=-32$
- $latex V_{z}=5$
Ahora, calculamos la magnitud con los componentes dados:
$latex |V| = \sqrt{V_{x}^2+V_{y}^2+V_{z}^2}$
$latex = \sqrt{(-40)^2 + (-32)^2+5^2} $
$latex = \sqrt{1600 + 1024+25}$
$latex = \sqrt{2649}$
$latex |V| = 51.47$
La distancia entre la posición inicial y final del avión es de 51.47 kilómetros.
Magnitud de vectores 2D y 3D – Ejercicios para resolver
¿Cuál es la magnitud del vector $latex \vec{A}=-8i+7j-9k$?
Escribe la respuesta usando dos decimales.
Véase también
¿Interesado en aprender más sobre vectores? Puedes mirar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
