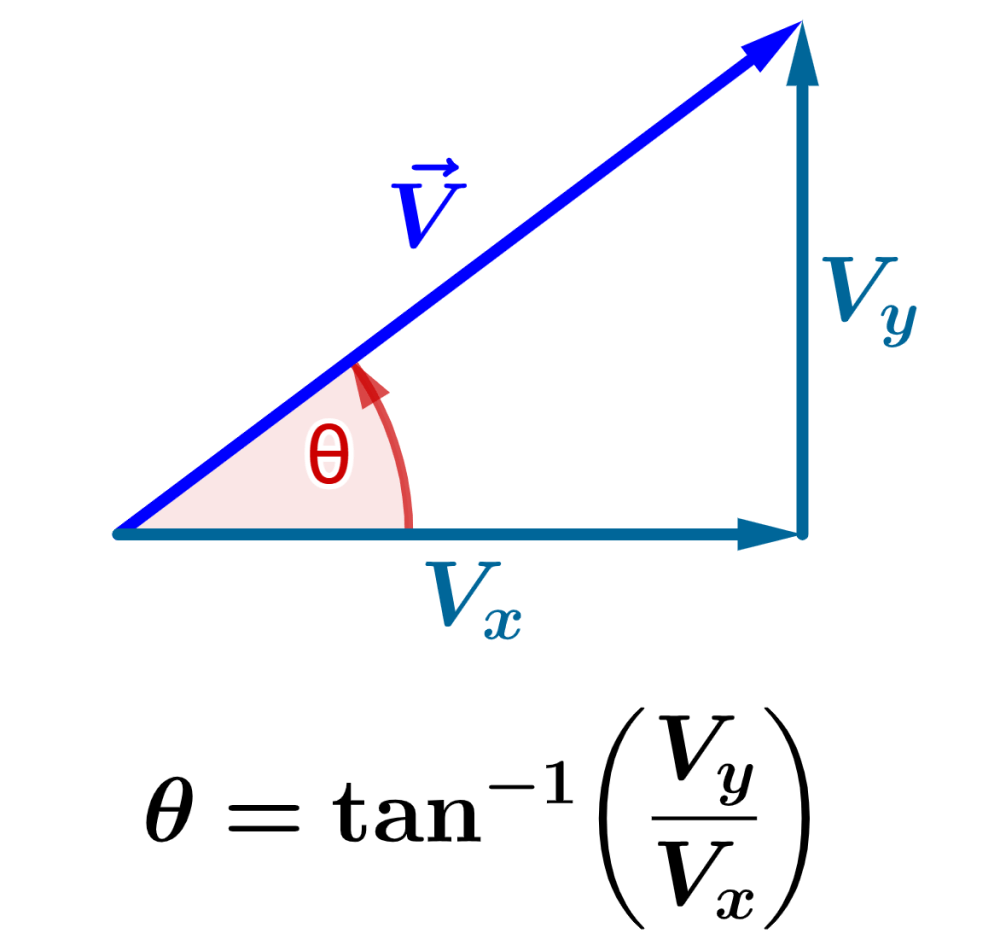La dirección de un vector es la orientación del vector en un sistema de coordenadas, normalmente descrita por el ángulo que forma con uno de los ejes. Para encontrar la dirección de un vector 2D, calculamos la tangente inversa del componente en y del vector sobre el componente en x.
En este artículo, conoceremos la fórmula que podemos aplicar para encontrar la dirección de un vector. Aprenderemos a derivar esta fórmula y la usaremos para resolver algunos ejercicios de práctica.
¿Cómo calcular la dirección de un vector 2D?
En un sistema de coordenadas cartesianas 2D (plano $latex x, ~y$), la dirección de un vector puede especificarse mediante el ángulo que forma con el eje $latex x$ positivo.
Este ángulo se mide normalmente en el sentido contrario a las agujas del reloj, siendo el rango de ángulos posibles de 0° a 360° (0 a 2π radianes).
Para calcular el ángulo de un vector utilizando sus componentes, podemos usar trigonometría, específicamente, la función tangente.
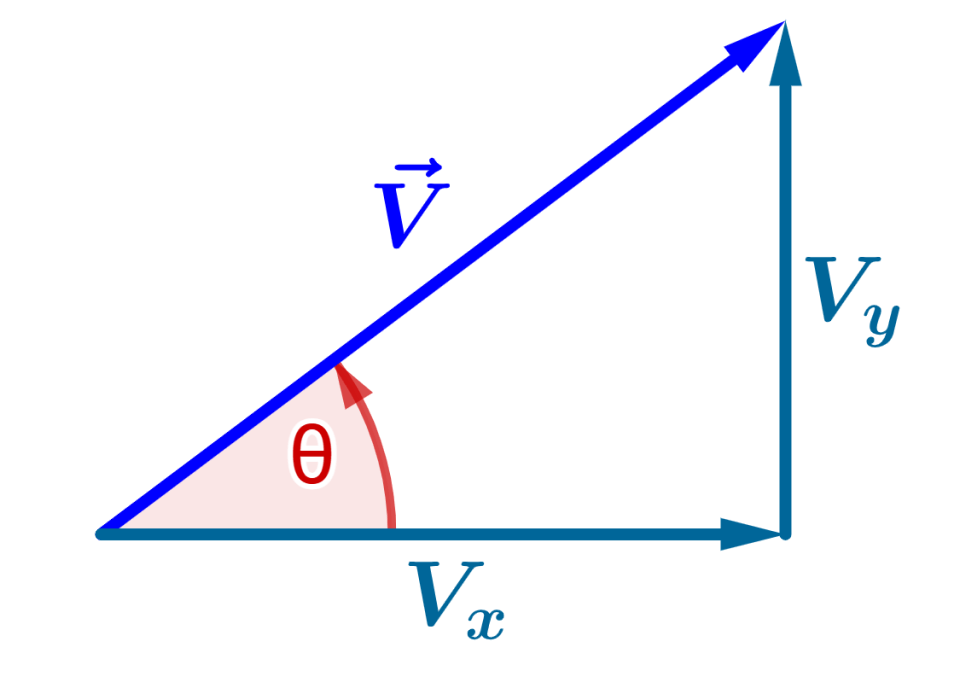
Supongamos que tenemos el vector $latex \vec{V}$ con los componentes $latex V_{x}$ y $latex V_{y}$ y el ángulo $latex \theta$:
Podemos observar que tenemos un triángulo rectángulo, en donde el vector $latex \vec{V}$ es la hipotenusa. El lado adyacente (base) es igual a $latex V_{x}$, y el lado opuesto (altura) es $latex V_{y}$.
Según la definición de la función tangente en un triángulo rectángulo, tenemos:
$$\tan(\theta) = \frac{\text{opuesto}}{\text{adyacente}}$$
En este caso,
$$\tan(\theta) = \frac{V_{y}}{V_{x}}$$
Para encontrar θ, tenemos que tomar la tangente inversa (también llamada arctangente o atan) de ambos lados de la ecuación. Entonces,
$$\theta = \tan^{-1}\left(\frac{V_{y}}{ V_{x}}\right)$$
Es importante tener en cuenta el cuadrante en el que se encuentra el vector, ya que la función tangente inversa devuelve un resultado comprendido entre $latex -\frac{\pi}{2}$ y $latex \frac{\pi}{2}$ (-90° a 90°).
Entonces, usamos la siguiente tabla para obtener el ángulo correcto:
| Cuadrante | Valor de $latex \tan^{-1}$ |
| I | Usamos el valor de la calculadora |
| II | Sumamos 180° (π) al valor de la calculadora |
| III | Sumamos 180° (π) al valor de la calculadora |
| IV | Sumamos 360° (2π) al valor de la calculadora |
Ejercicios resueltos de la dirección de un vector
EJERCICIO 1
Encuentra el ángulo $latex \theta $ del vector $latex \vec{A}$ con componentes $latex A_{x} = 3$ y $latex A_{y} = 4$.
Solución
Tenemos los siguientes componentes:
- $latex A_{x}=3$
- $latex A_{y}=4$
Entonces, usamos la fórmula del ángulo o dirección de un vector:
$$\theta = \tan^{-1}\left(\frac{A_{y}}{ A_{x}}\right)$$
$$\theta = \tan^{-1}\left(\frac{4}{3}\right)$$
Usando una calculadora, obtenemos:
$latex \theta \approx 53.13^{\circ}$
Por lo tanto, el ángulo del vector A con respecto al eje $latex x$ positivo es de aproximadamente 53.13°.
EJERCICIO 2
¿Cuál es el ángulo $latex \theta $ del vector $latex \vec{B}$ que tiene componentes $latex B_{x} = -5$ y $latex B_{y} = 12$?
Solución
Podemos observar la siguiente información:
- $latex B_{x}=-5$
- $latex B_{y}=12$
Al aplicar la fórmula del ángulo con estos componentes, tenemos:
$$\theta = \tan^{-1}\left(\frac{V_{y}}{ V_{x}}\right)$$
$$\theta = \tan^{-1}\left(\frac{12}{-5}\right)$$
Usando una calculadora, obtenemos:
$latex \theta \approx -67.38^{\circ}$
Sin embargo, como el vector está en el segundo cuadrante ($latex x$ negativo, $latex y$ positivo), debemos sumar 180° al resultado:
$latex \theta = -67.38^{\circ} + 180^{\circ} $
$latex \theta = 112.62^{\circ}$
Por lo tanto, el ángulo del vector B con respecto al eje $latex x$ positivo es de aproximadamente 112.62°.
EJERCICIO 3
Calcula el ángulo $latex \theta $ del vector $latex \vec{C}$ que tiene los componentes $latex C_{x} = -6$ y $latex C_{y} = -8$.
Solución
Podemos obtener la siguiente información:
- $latex C_{x}=-6$
- $latex C_{y}=-8$
Al sustituir estos valores en la fórmula del ángulo de un vector, tenemos:
$$\theta = \tan^{-1}\left(\frac{C_{y}}{ C_{x}}\right)$$
$$\theta = \tan^{-1}\left(\frac{-8}{-6}\right)$$
Usando una calculadora, obtenemos:
$latex \theta \approx 53.13^{\circ}$
Como el vector está en el tercer cuadrante ($latex x$ negativo, $latex y$ negativo), debemos sumar 180° al resultado:
$latex \theta = 53.13^{\circ} + 180^{\circ} $
$latex \theta = 233.13^{\circ}$
EJERCICIO 4
¿Cuál es el ángulo $latex \theta $ del vector $latex \vec{D}$ con componentes $latex D_{x} = 7$ y $latex D_{y} = -3$?
Solución
Podemos extraer la siguiente información:
- $latex D_{x}=7$
- $latex D_{y}=-3$
El ángulo del vector es igual a:
$$\theta = \tan^{-1}\left(\frac{D_{y}}{ D_{x}}\right)$$
$$\theta = \tan^{-1}\left(\frac{-3}{7}\right)$$
Usando una calculadora, obtenemos:
$latex \theta \approx -23.2^{\circ}$
Como el vector está en el cuarto cuadrante ($latex x$ positivo, $latex y$ negativo), podemos sumar 360° al resultado:
$latex \theta = -23.2^{\circ} + 360^{\circ}$
$latex \theta = 336.8^{\circ}$
EJERCICIO 5
Si es que un vector tiene los componentes $latex A_{x} = -10$ y $latex A_{y} = 0$, ¿cuál es su ángulo $latex \theta$?
Solución
En este caso, tenemos un componente $latex y $ igual a cero, por lo que al usar la función tangente inversa, obtendremos un ángulo igual a cero.
Podemos resolver este problema al considerar que el componente $latex x$ es negativo. Entonces, sabemos que el ángulo formado debe ser igual a 180°.
$latex \theta =180^{\circ}$
Cuando tenemos problemas similares a este, es útil considerar la posición en los ejes del plano cartesiano.
EJERCICIO 6
Encuentra el ángulo $latex \theta $ del vector $latex \vec{G}$ con los componentes $latex G_{x} = 8$ y $latex G_{y} = 15$.
Solución
Tenemos los siguientes componentes:
- $latex G_{x}=8$
- $latex G_{y}=15$
Entonces, usamos la fórmula del ángulo o dirección de un vector:
$$\theta = \tan^{-1}\left(\frac{G_{y}}{ G_{x}}\right)$$
$$\theta = \tan^{-1}\left(\frac{15}{8}\right)$$
Usando una calculadora, obtenemos:
$latex \theta \approx 61.93^{\circ}$
EJERCICIO 7
¿Cuál es el ángulo $latex \theta $ del vector $latex \vec{H}$ con componentes $latex H_{x} = -12$ y $latex H_{y} = -5$?
Solución
Podemos observar lo siguiente:
- $latex H_{x}=-12$
- $latex H_{y}=-5$
Al aplicar la fórmula del ángulo de un vector 2D, tenemos:
$$\theta = \tan^{-1}\left(\frac{H_{y}}{ H_{x}}\right)$$
$$\theta = \tan^{-1}\left(\frac{-5}{-12}\right)$$
Usando una calculadora, obtenemos:
$latex \theta \approx 22.62^{\circ}$
Como el vector está en el tercer cuadrante ($latex x$ negativo, $latex y$ negativo), debemos sumar 180° al resultado:
$latex \theta = 22.62^{\circ} + 180^{\circ}$
$latex \theta = 202.62^{\circ}$
EJERCICIO 8
Un avión vuela con rumbo norte a una velocidad de 150 km/h. Hay un fuerte viento del oeste que empuja el avión hacia el este con una velocidad de 40 km/h. ¿Cuál es la dirección del avión con respecto al suelo?
Solución
Vamos a representar a la velocidad del avión con $latex \vec{A}$ a la velocidad del viento con $latex \vec{V}$.
Como el avión vuela con rumbo norte, sus componentes de velocidad son $latex A_{x}$ = 0$ km/h y $latex A_{y} = 150$ km/h. El viento sopla del oeste, por lo que sus componentes de velocidad son $latex V_{x} = 40$ km/h y $latex V_{y} = 0$ km/h.
Para hallar la velocidad y la dirección reales del avión con respecto al suelo, $latex \vec{R}$, tenemos que sumar las componentes de la velocidad del avión y las componentes de la velocidad del viento:
$latex R_{x} = A_{x} + V_{x} = 0 + 40 = 40$ km/h
$latex R_{y} = R_{y} + V_{y} = 150 + 0 = 150$ km/h
Ahora, usamos la fórmula del ángulo con estos componentes:
$$\theta = \tan^{-1}\left(\frac{R_{y}}{ R_{x}}\right)$$
$$\theta = \tan^{-1}\left(\frac{150}{40}\right)$$
$latex \theta \approx 75.62^{\circ}$
Como el ángulo se mide desde el eje $latex x$ positivo (este), el avión vuela aproximadamente 75.96° al norte del este.
Dirección de vectores 2D – Ejercicios para resolver
Encuentra el ángulo θ de un vector que tiene los componentes $latex V_{x}=0$ y $latex V_{y}=-14$.
Escribe el ángulo en grados.
Véase también
¿Interesado en aprender más sobre vectores? Puedes mirar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
