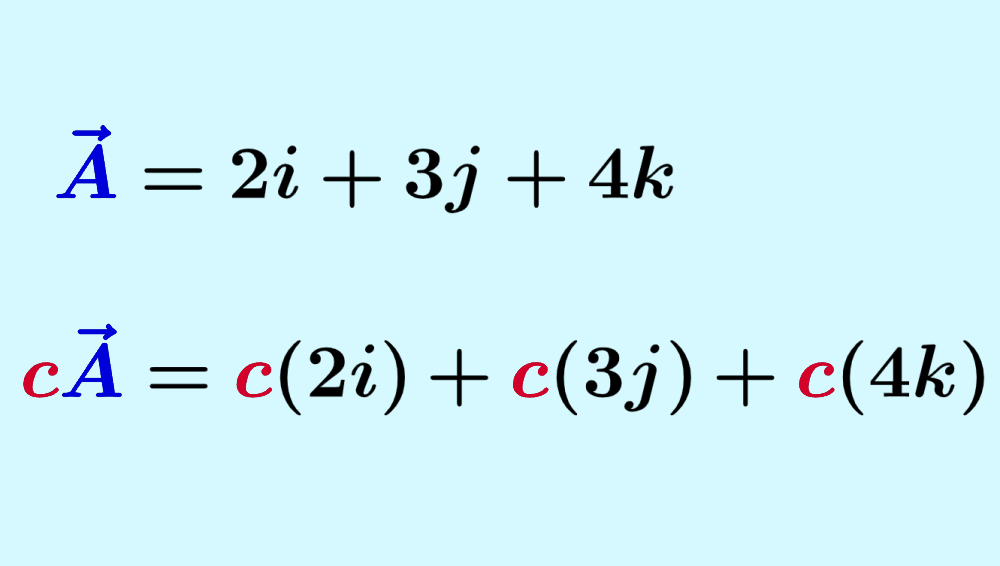La multiplicación de un vector por un escalar es resuelta simplemente al multiplicar a la magnitud por el escalar. Esto también es equivalente a multiplicar a cada uno de los componentes del vector por el escalar.
A continuación, aprenderemos sobre la multiplicación de un vector por un escalar más en detalle. Resolveremos algunos ejercicios y problemas de práctica para aplicar lo aprendido.
¿Cómo multiplicar a un vector por un escalar?
Para multiplicar a un vector por un escalar, solo tenemos que multiplicar a su magnitud por el escalar. Alternativamente, multiplicamos a cada uno de los componentes por el escalar.
Cuando multiplicamos a un vector por un escalar positivo, cambiamos su magnitud, pero no su dirección:
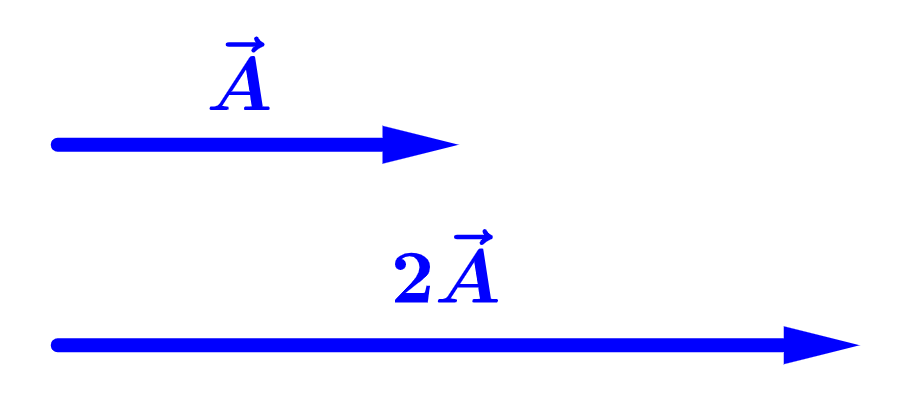
Cuando multiplicamos a un vector por un escalar negativo, cambiamos su magnitud y revertimos su dirección:
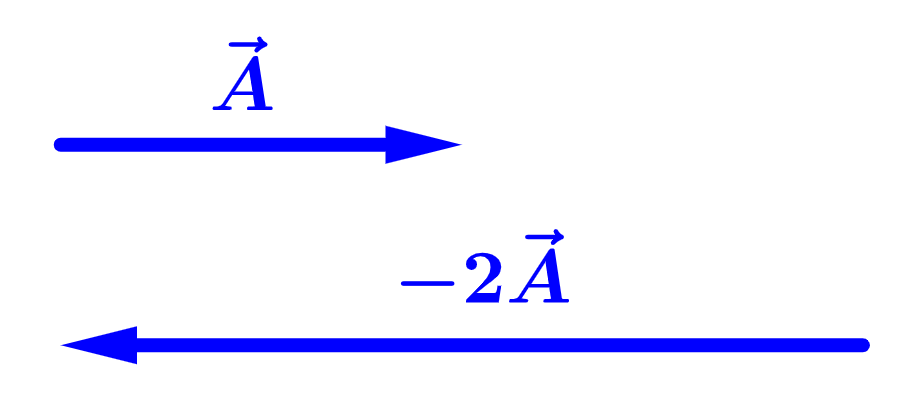
Si es que multiplicamos a un vector $latex \vec{A}$ por un escalar $latex k$, cada componente del producto $latex \vec{R}=k \vec{A}$, es el producto de $latex k$ y el componente correspondiente de $latex \vec{A}$:
$latex R_{x}=kA_{x}$
$latex R_{y}=kA_{y}$
Ten en cuenta que los componentes no son vectores. Los componentes de un vector son números y no vectores. Por esta razón, usamos letras sin flechas encima para representarlos.
Ejercicios resueltos de multiplicación de un vector por un escalar
EJERCICIO 1
Multiplica al vector $latex \vec{A} = 5i -2j+ 3k$ por el escalar $latex k = 4$.
Solución
Multiplicamos a cada componente del vector A por el escalar $latex k$:
$latex 5i \times 4 = 20i$
$latex -2j \times 4 = -8j$
$latex 3k \times 4 = 12k$
El vector resultante es: $latex \vec{R}= 20i -8j+ 12k$.
EJERCICIO 2
Encuentra el producto del vector $latex \vec{B} = -1i+ 6j+ 0k$ por el escalar $latex k = -3$
Solución
Al multiplicar a cada componente del vector B por el escalar $latex k$, tenemos:
$latex -1i \times -3 = 3i$
$latex 6j \times -3 = -18j$
$latex 0k \times -3 = 0k$
El vector resultante es: $latex \vec{R}= 3i -18j+ 0k$.
EJERCICIO 3
Multiplica al vector $latex \vec{C} = 3i -4j +7k$ por el escalar $latex k = 0.5$.
Solución
Cuando multiplicamos a cada componente del vector C por el escalar $latex k$, tenemos:
$latex 3i \times 0.5 = 1.5i$
$latex -4j \times 0.5 = -2j$
$latex 7k \times 0.5 = 3.5k$
El vector resultante es: $latex \vec{R}= 1.5i -2j+ 3.5k$.
EJERCICIO 4
¿Cuál es el resultado al multiplicar al vector $latex \vec{D} = 2i -5j+ 4k$ por el escalar $latex k = 3$.
Solución
Al multiplicar al escalar $latex k$ por cada componente del vector dado, tenemos:
$latex 2i \times 3 = 6i$
$latex -5j \times 3 = -15j$
$latex 4k \times 3 = 12k$
El vector resultante es: $latex \vec{R}= 6i -15j+ 12k$.
EJERCICIO 5
Multiplica al vector $latex \vec{E} = 7i+ 0j -3k$ por el escalar $latex k = -2$
Solución
Cuando multiplicamos a cada componente del vector E por el escalar $latex k$, tenemos:
$latex 7i \times -2 = -14i$
$latex 0j \times -2 = 0j$
$latex -3k \times -2 = 6k$
El vector resultante es: $latex \vec{R}= -14i +0j+ 6k$.
EJERCICIO 6
Multiplica al vector $latex \vec{F} = -4i+ 3j+ 8k$ por el escalar: $latex k = 0.25$
Solución
Al distribuir la multiplicación del escalar $latex k$ a cada componente del vector, tenemos:
$latex -4i \times 0.25 = -1i$
$latex 3j \times 0.25 = 0.75j$
$latex 8k \times 0.25 = 2k$
El vector resultante es: $latex \vec{R}= -i +0.75j+ 2k$.
Multiplicar vectores por un escalar – Ejercicios para resolver
Si es que la magnitud de un vector es 17 unidades y multiplicamos al vector por 2.5, ¿cuál es la magnitud del nuevo vector?
Escribe la respuesta en la casilla.
Véase también
¿Interesado en aprender más sobre vectores? Puedes mirar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
