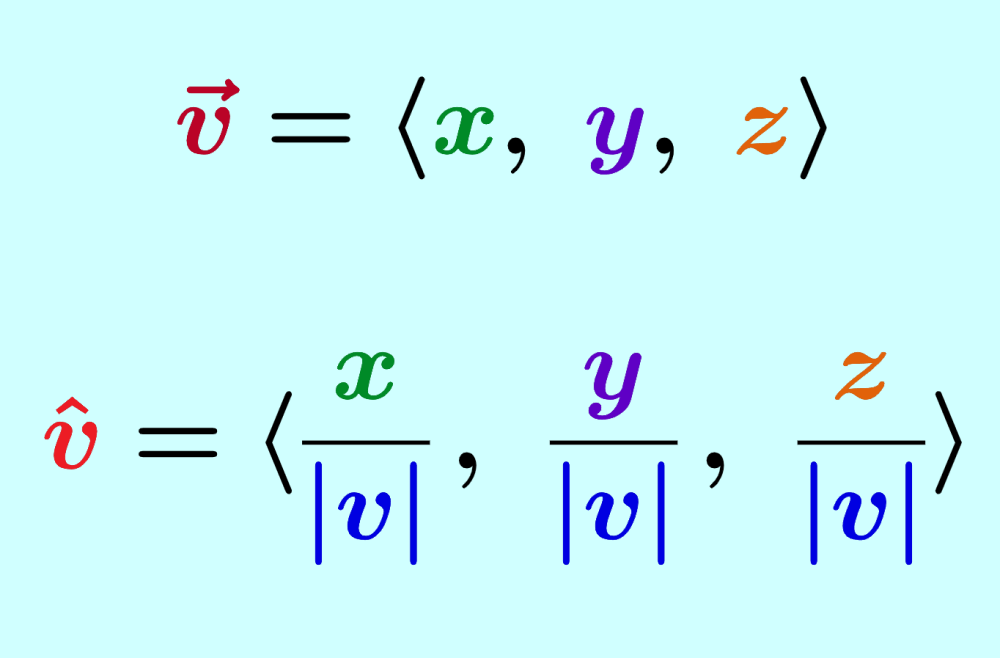Los vectores unitarios son vectores que tienen una magnitud de 1 y no tienen unidades. Estos vectores son usados para describir una dirección en el espacio. Para encontrar el vector unitario de un vector, dividimos a cada componente por su magnitud.
A continuación, aprenderemos a calcular vectores unitarios de vectores. Conoceremos las fórmulas que podemos usar y las aplicaremos para resolver algunos ejercicios de práctica.
¿Cómo encontrar el vector unitario de un vector?
Para encontrar el vector unitario de un vector dado, tenemos que normalizar el vector original. Un vector unitario es un vector con una magnitud (longitud) de 1, que apunta en la misma dirección que el vector original.
Entonces, podemos seguir dos pasos simples para encontrar el vector unitario:
Paso 1: Calcula la magnitud (longitud) del vector original: Para un vector $latex \vec{V} = \langle x, y, z\rangle$, la magnitud está dada por:
$latex |V| = \sqrt{x^2 + y^2 + z^2}$
Paso 2: Divide a cada componente del vector original por su magnitud:
$$\hat{V} = \frac{\vec{V}}{|V|}$$
$$= \langle \frac{x}{|V|}, ~\frac{y}{|V|}, ~\frac{z}{|V|}\rangle$$
Nota: Usamos la notación (^) o «sombrero» sobre la letra que representa a vectores unitarios. Esto nos permite distinguirlos de vectores normales.
10 Ejercicios resueltos de vectores unitarios
EJERCICIO 1
Encuentra el vector unitario del vector $latex \vec{A} = \langle 3, ~4 \rangle$.
Solución
Empezamos calculando la magnitud del vector:
$$|A| = \sqrt{3^2 + 4^2} =$$
$$ \sqrt{9 + 16} = \sqrt{25} = 5$$
Ahora, normalizamos al vector original:
$$\hat{A} = \left\langle \frac{3}{5}, ~\frac{4}{5} \right\rangle $$
$$= \langle 0.6, ~0.8 \rangle$$
El vector unitario de $latex \vec{A} = \langle 3, ~4 \rangle$ es $latex \hat{A} = \langle 0.6, ~0.8 \rangle$.
EJERCICIO 2
¿Cuál es el vector unitario de $latex \vec{B} = \langle -6, ~8 \rangle$?
Solución
Al calcular la magnitud del vector, tenemos:
$$|B| = \sqrt{(-6)^2 + 8^2} $$
$$= \sqrt{36 + 64} = \sqrt{100} = 10$$
Al normalizar al vector, tenemos:
$$\hat{B} = \left\langle \frac{-6}{10}, ~\frac{8}{10} \right\rangle $$
$$= \langle -0.6, ~0.8 \rangle$$
El vector unitario de $latex \vec{B} = \langle -6, ~8 \rangle$ es $latex \hat{B} = \langle -0.6, ~0.8 \rangle$.
EJERCICIO 3
Encuentra el vector unitario del vector $latex \vec{C} = \langle 5, ~12 \rangle$.
Solución
Empezamos calculando la magnitud del vector dado:
$$|C| = \sqrt{5^2 + 12^2} $$
$$= \sqrt{25 + 144} = \sqrt{169} = 13$$
Ahora, dividimos a cada componente del vector por la magnitud:
$$ \hat{C} = \left\langle \frac{5}{13},~ \frac{12}{13} \right\rangle $$
$$= \langle \frac{5}{13}, ~\frac{12}{13} \rangle$$
$$ \approx \langle 0.385, ~0.923 \rangle$$
El vector unitario de $latex \vec{C} = \langle 5,~ 12 \rangle$ es $latex \hat{C} \approx \langle 0.385, ~0.923 \rangle$.
EJERCICIO 4
¿Cuál es el vector unitario del vector $latex \vec{A} = \langle 2,~ -4, ~1 \rangle$?
Solución
La magnitud del vector $latex \vec{A}$ es:
$$|A| = \sqrt{2^2 + (-4)^2 + 1^2} $$
$$= \sqrt{4 + 16 + 1} = \sqrt{21}$$
Normalizando al vector, tenemos:
$$\hat{A} = \left\langle \frac{2}{\sqrt{21}}, ~\frac{-4}{\sqrt{21}}, ~\frac{1}{\sqrt{21}} \right\rangle $$
$$\approx \langle 0.44, -0.88, 0.22 \rangle$$
El vector unitario de $latex \vec{A} = \langle 2, ~-4, ~1 \rangle$ es $latex \hat{A} \approx \langle 0.44, ~-0.88,~ 0.22 \rangle$.
EJERCICIO 5
Si tenemos al vector $latex \vec{B} = \langle -3, ~6,~ 2 \rangle$, encuentra su vector unitario.
Solución
La magnitud del vector $latex \vec{B}$ es:
$$|B| = \sqrt{(-3)^2 + 6^2 + 2^2} $$
$$= \sqrt{9 + 36 + 4} = \sqrt{49} = 7$$
Cuando normalizamos al vector, tenemos:
$$\hat{B} = \left\langle \frac{-3}{7}, ~\frac{6}{7}, ~\frac{2}{7} \right\rangle$$
$$ \approx \langle -0.43, ~0.86,~ 0.29 \rangle$$
El vector unitario de $latex \vec{B} = \langle -3, ~6, ~2 \rangle$ es $latex \hat{B} \approx \langle -0.43,~ 0.86,~ 0.29 \rangle$.
.
EJERCICIO 6
Encuentra el vector unitario del vector $latex \vec{D} = \langle 4,~ -8, ~4 \rangle$.
Solución
Empezamos encontrando la magnitud del vector D:
$$|D| = \sqrt{4^2 + (-8)^2 + 4^2} $$
$$= \sqrt{16 + 64 + 16} = \sqrt{96} = 4\sqrt{6}$$
Ahora, dividimos a cada componente por la magnitud del vector:
$$\hat{D} = \left\langle \frac{4}{4\sqrt{6}}, ~\frac{-8}{4\sqrt{6}}, ~\frac{4}{4\sqrt{6}} \right\rangle $$
$$= \langle \frac{1}{\sqrt{6}},~ \frac{-2}{\sqrt{6}},~ \frac{1}{\sqrt{6}} \rangle $$
$$\approx \langle 0.41, ~-0.82,~ 0.41 \rangle$$
El vector unitario de $latex \vec{D} = \langle 4,~ -8,~ 4 \rangle$ es $latex \hat{D} \approx \langle 0.41,~ -0.82,~ 0.41 \rangle$.
EJERCICIO 7
¿Cuál es el vector unitario del vector $latex \vec{E} = \langle -6, ~3, ~9 \rangle$?
Solución
Encontramos la magnitud del vector:
$$|E| = \sqrt{(-6)^2 + 3^2 + 9^2} $$
$$= \sqrt{36 + 9 + 81} = \sqrt{126} = 3\sqrt{14}$$
Cuando dividimos a cada componente por la magnitud, tenemos:
$$\hat{E} = \left\langle \frac{-6}{3\sqrt{14}}, ~\frac{3}{3\sqrt{14}},~ \frac{9}{3\sqrt{14}} \right\rangle$$
$$ = \langle \frac{-2}{\sqrt{14}}, ~\frac{1}{\sqrt{14}}, ~\frac{3}{\sqrt{14}} \rangle$$
$$ \approx \langle -0.53,~ 0.27, ~0.80 \rangle$$
El vector unitario de $latex \vec{E} = \langle -6, ~3, ~9 \rangle$ es $latex \hat{E} \approx \langle -0.53, ~0.27,~ 0.80 \rangle$.
EJERCICIO 8
Encuentra el vector unitario del vector $latex \vec{G} = \langle 5, ~10, ~-5 \rangle$.
Solución
La magnitud del vector dado es:
$$|G| = \sqrt{5^2 + 10^2 + (-5)^2} $$
$$= \sqrt{25 + 100 + 25} = \sqrt{150} = 5\sqrt{6}$$
Al normalizar el vector, tenemos:
$$\hat{G} = \left\langle \frac{5}{5\sqrt{6}},~ \frac{10}{5\sqrt{6}},~ \frac{-5}{5\sqrt{6}} \right\rangle $$
$$= \langle \frac{1}{\sqrt{6}}, ~\frac{2}{\sqrt{6}},~ \frac{-1}{\sqrt{6}} \rangle$$
$$ \approx \langle 0.41,~ 0.82, ~-0.41 \rangle$$
El vector unitario de $latex \vec{G} = \langle 5,~ 10, ~-5 \rangle$ es $latex \hat{G} \approx \langle 0.41,~ 0.82,~ -0.41 \rangle$.
EJERCICIO 9
Si tenemos al vector $latex \vec{A} = \langle 2,~ 4,~ -4 \rangle$, encuentra su vector unitario.
Solución
Encontramos la magnitud del vector A:
$$|A| = \sqrt{2^2 + 4^2 + (-4)^2} $$
$$= \sqrt{4 + 16 + 16} = \sqrt{36} = 6$$
Dividimos a cada componente del vector por su magnitud:
$$\hat{A} = \left\langle \frac{2}{6},~ \frac{4}{6},~ \frac{-4}{6} \right\rangle $$
$$= \langle \frac{1}{3}, ~\frac{2}{3}, ~-\frac{2}{3} \rangle $$
$$\approx \langle 0.333, ~0.667, ~-0.667 \rangle$$
El vector unitario de $latex \vec{A} = \langle 2, ~4,~ -4 \rangle$ es $latex \hat{A} \approx \langle 0.333, ~0.667,~ -0.667 \rangle$.
EJERCICIO 10
Encuentra el vector unitario del vector $latex \vec{B} = \langle -3, ~6, ~9 \rangle$.
Solución
Calculamos la magnitud del vector dado:
$$|B| = \sqrt{(-3)^2 + 6^2 + 9^2} $$
$$= \sqrt{9 + 36 + 81} = \sqrt{126} = 3\sqrt{14}$$
Al normalizar al vector, tenemos:
$$\hat{B} = \left\langle \frac{-3}{3\sqrt{14}}, ~\frac{6}{3\sqrt{14}},~ \frac{9}{3\sqrt{14}} \right\rangle $$
$$= \langle \frac{-1}{\sqrt{14}}, ~\frac{2}{\sqrt{14}},~ \frac{3}{\sqrt{14}} \rangle $$
$$\approx \langle -0.27,~ 0.53, ~0.80 \rangle$$
El vector unitario de $latex \vec{B} = \langle -3, ~6, ~9 \rangle$ es $latex \hat{B} \approx \langle -0.27,~ 0.53, ~0.80 \rangle$.
Vectores unitarios – Ejercicios para resolver
Véase también
¿Interesado en aprender más sobre vectores? Puedes mirar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
