Dos o más vectores pueden ser sumados usando tanto métodos gráficos, como métodos algebraicos. Los tres métodos principales para sumar vectores son: el método del polígono, el método del paralelogramo y suma de vectores por sus componentes.
A continuación, veremos algunos ejercicios resueltos y ejercicios para resolver de suma de vectores. Usaremos los tres métodos mencionados.
10 Ejercicios resueltos de suma de vectores
Si necesitas hacer una revisión de los métodos para sumar vectores, puedes visitar este artículo.
EJERCICIO 1
Encuentra la suma de los siguientes vectores usando el método del polígono:
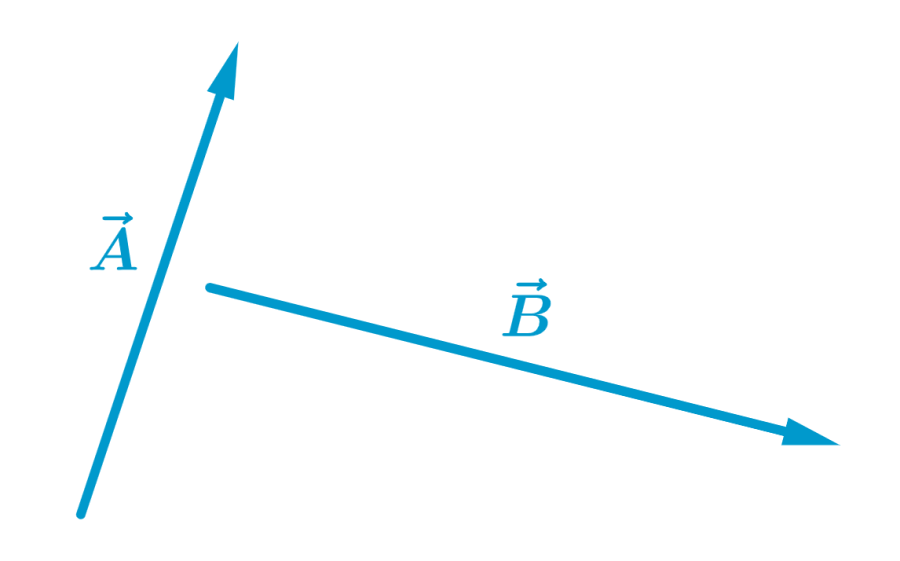
Solución
Para encontrar la suma de los vectores por el método del polígono, tenemos que colocar a la base de uno de los vectores en la punta o cabeza del otro vector.
Entonces, colocamos a la base del vector $latex \vec{B}$ en la cabeza del vector $latex \vec{A}$:
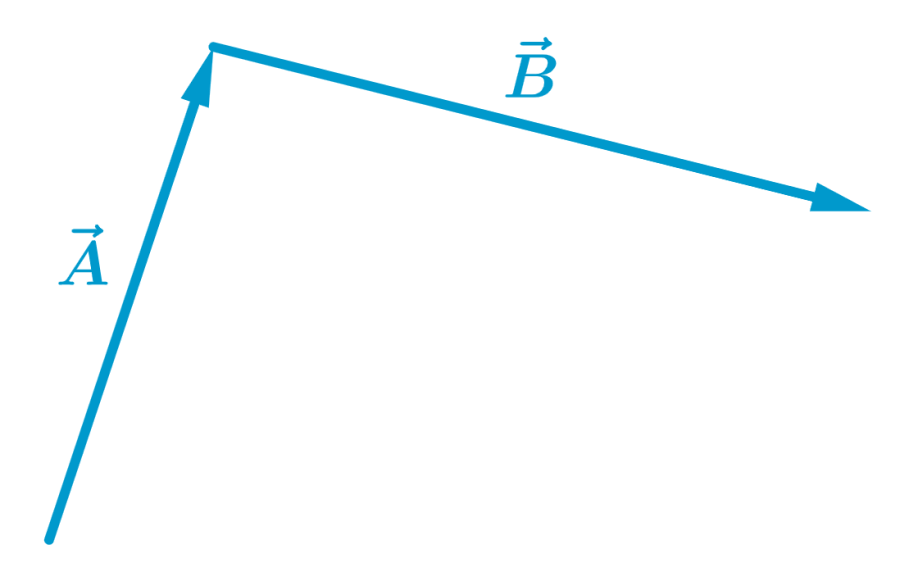
El vector resultante, $latex \vec{R}$, es el vector que une la base o cola del primer vector a la cabeza del segundo vector:
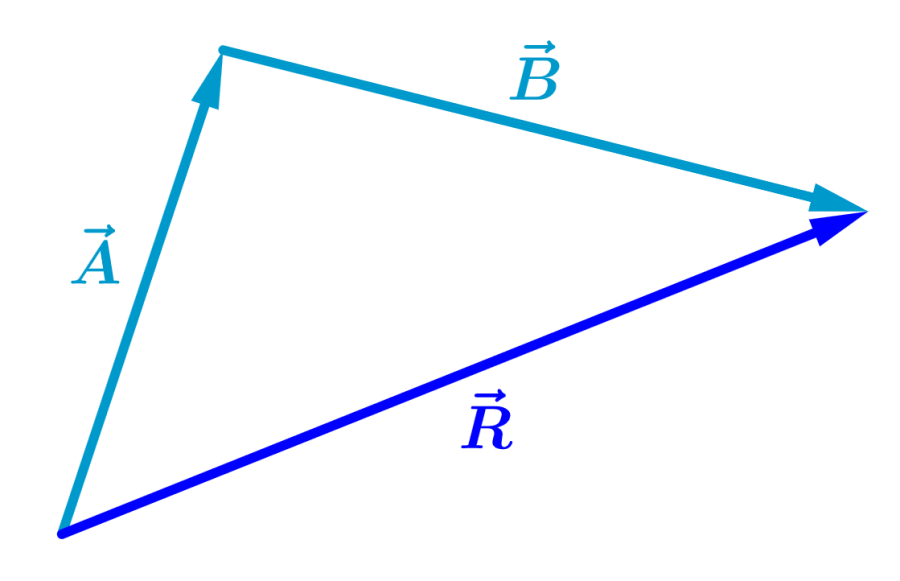
El orden en el que sumemos no importa. Es decir, podemos intercambiar a los vectores y obtener el mismo resultado:
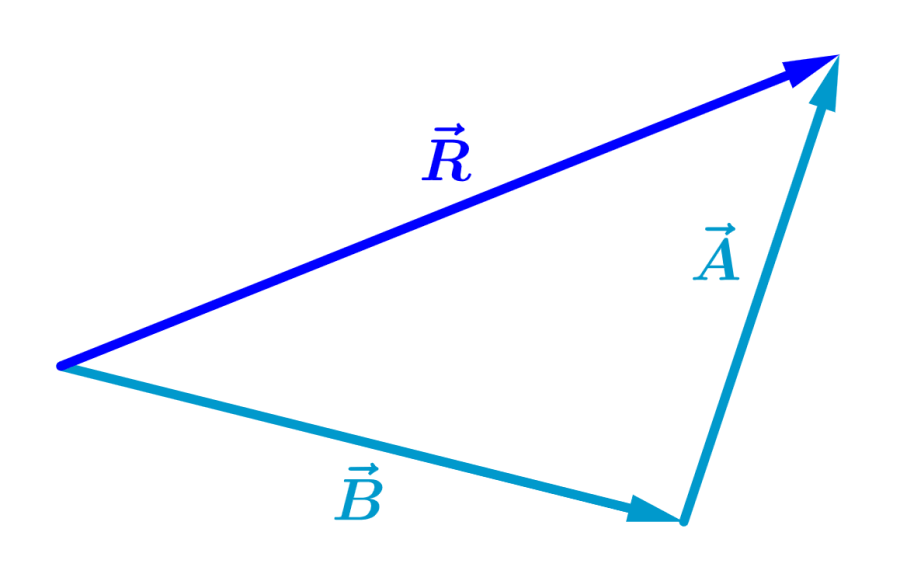
.
EJERCICIO 2
Encuentra la suma de los siguientes tres vectores usando el método del polígono:
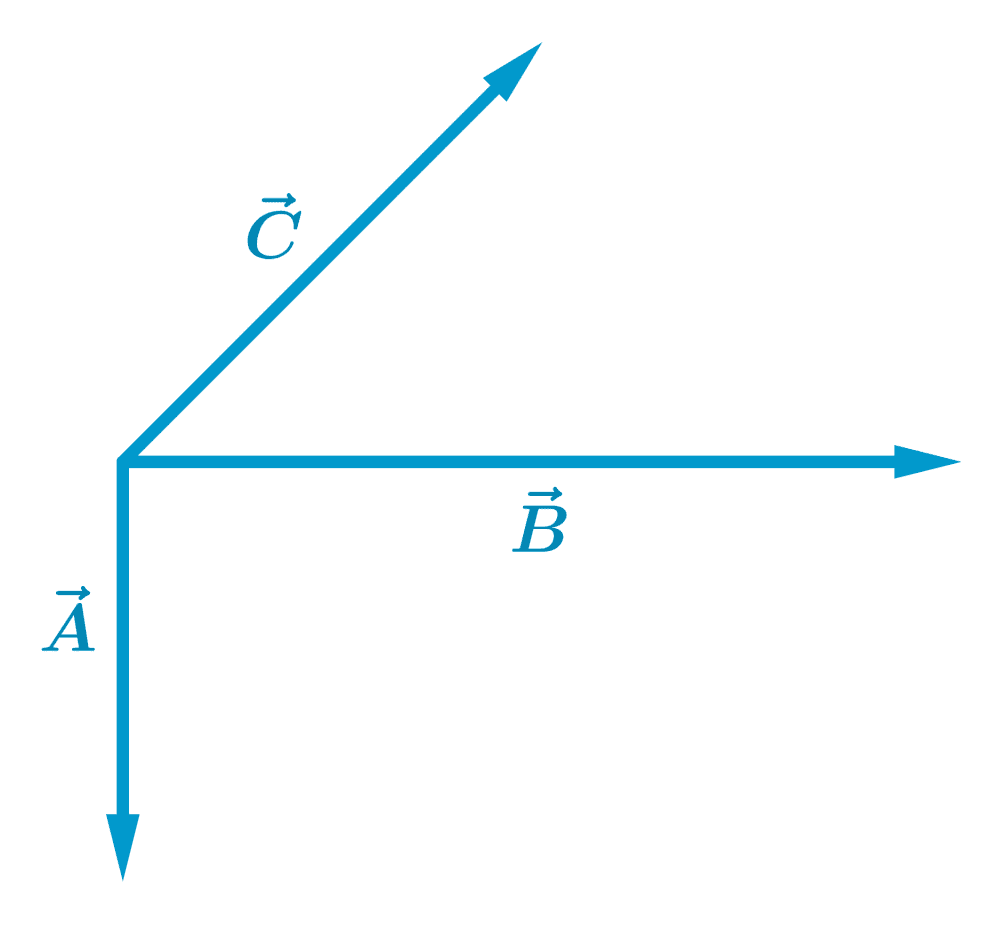
Solución
Vamos a empezar sumando dos de los vectores y luego sumamos el vector resultante con el tercer vector.
Entonces, empezamos por sumar los vectores $latex \vec{A}$ y $latex \vec{B}$ para obtener el vector $latex \vec{D}$:
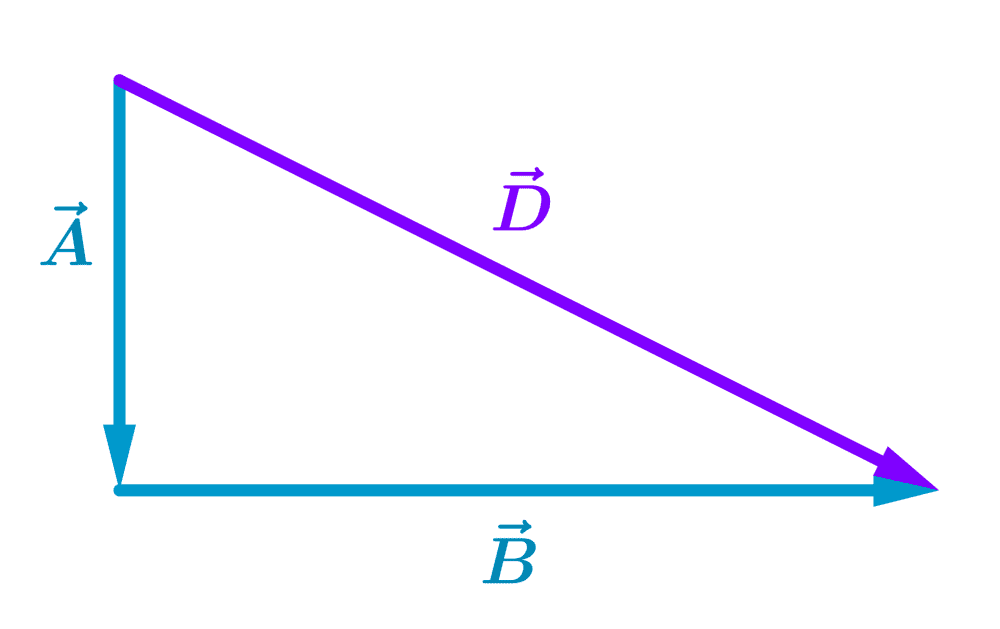
Ahora, sumamos el vector $latex \vec{C}$ al vector $latex \vec{D}$ para obtener el resultado final $latex \vec{R}$:
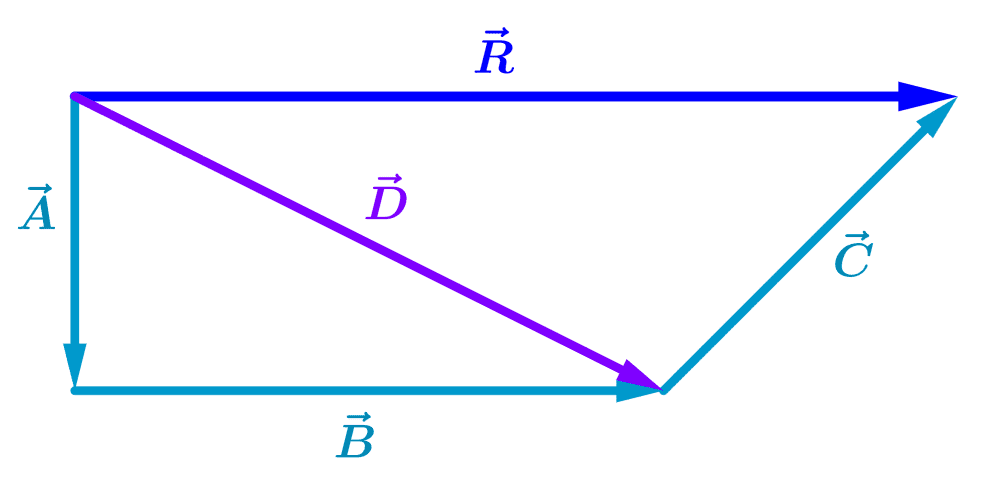
Similar al ejemplo anterior, la suma puede realizarse en cualquier otro orden.
EJERCICIO 3
Carlos sale a dar un paseo en su bicicleta. Él decide viajar 10 km hacia el Norte y luego 20 km hacia el Este. Encuentra la distancia y la dirección de su posición final.
Solución
Podemos usar un diagrama para representar a la suma de los vectores que indican el viaje de 10 km hacia el Norte y 20 km hacia el Este:
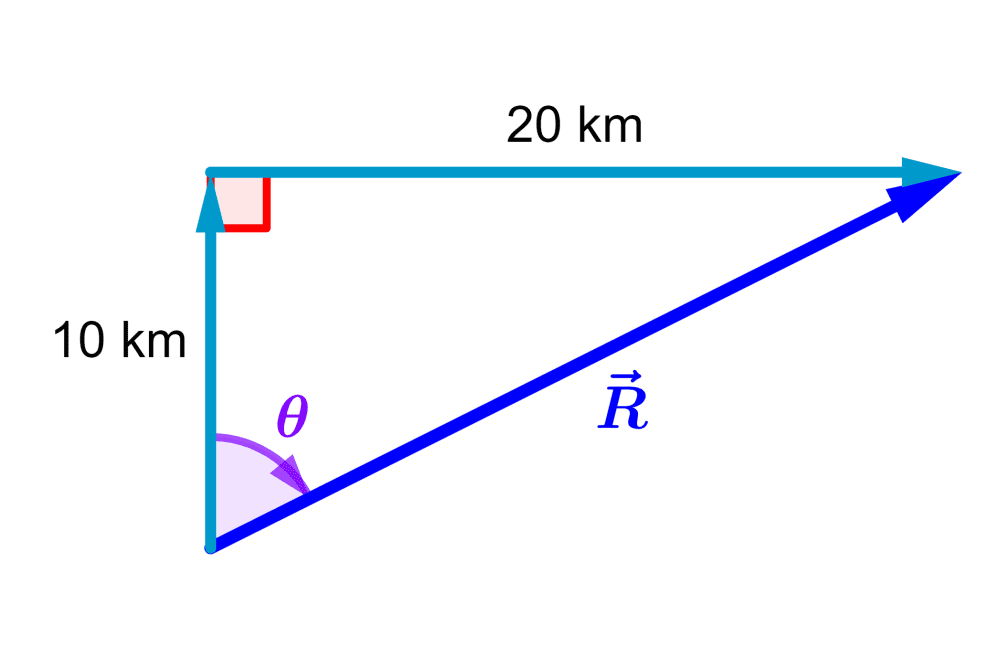
Entonces, la distancia y la dirección de su posición final son encontradas al determinar la magnitud (longitud) y el ángulo del vector $latex \vec{R}$.
Los vectores forman un ángulo recto el uno con el otro, por lo que el triángulo formado es un triángulo rectángulo y podemos usar el teorema de Pitágoras.
La distancia desde el punto inicial hasta el punto final es igual a la hipotenusa del triángulo y tenemos:
$$\sqrt{(10\text{ km})^2+(20\text{ km})^2}=22.36\text{ km}$$
Para encontrar el ángulo θ, usamos la función tangente:
$$\tan(\theta)=\frac{\text{opuesto}}{\text{adyacente}}=\frac{20\text{ km}}{10\text{ km}}=2$$
$$\theta=\tan^{-1}(2)=63.4^{\circ}$$
Entonces, Carlos está a 22.36 km en una dirección de 63.4° desde el norte hacia el este (eje x positivo).
EJERCICIO 4
Usa el método del paralelogramo para sumar los siguientes vectores:
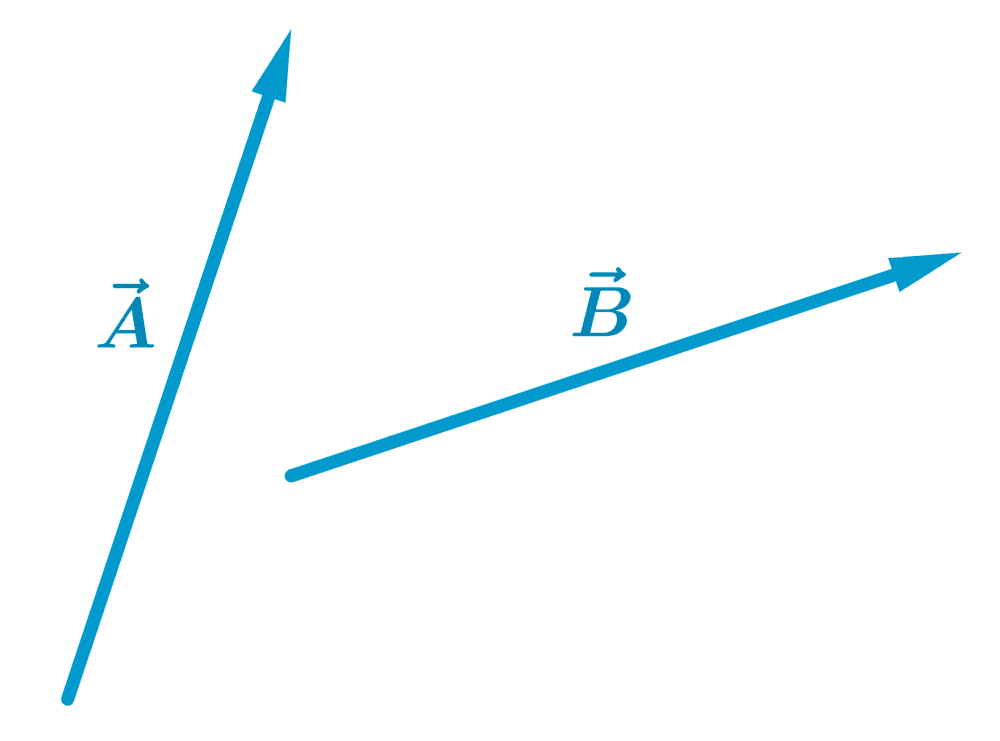
Solución
El método del paralelogramo consiste en colocar a los vectores con sus bases en el mismo punto de la siguiente forma:
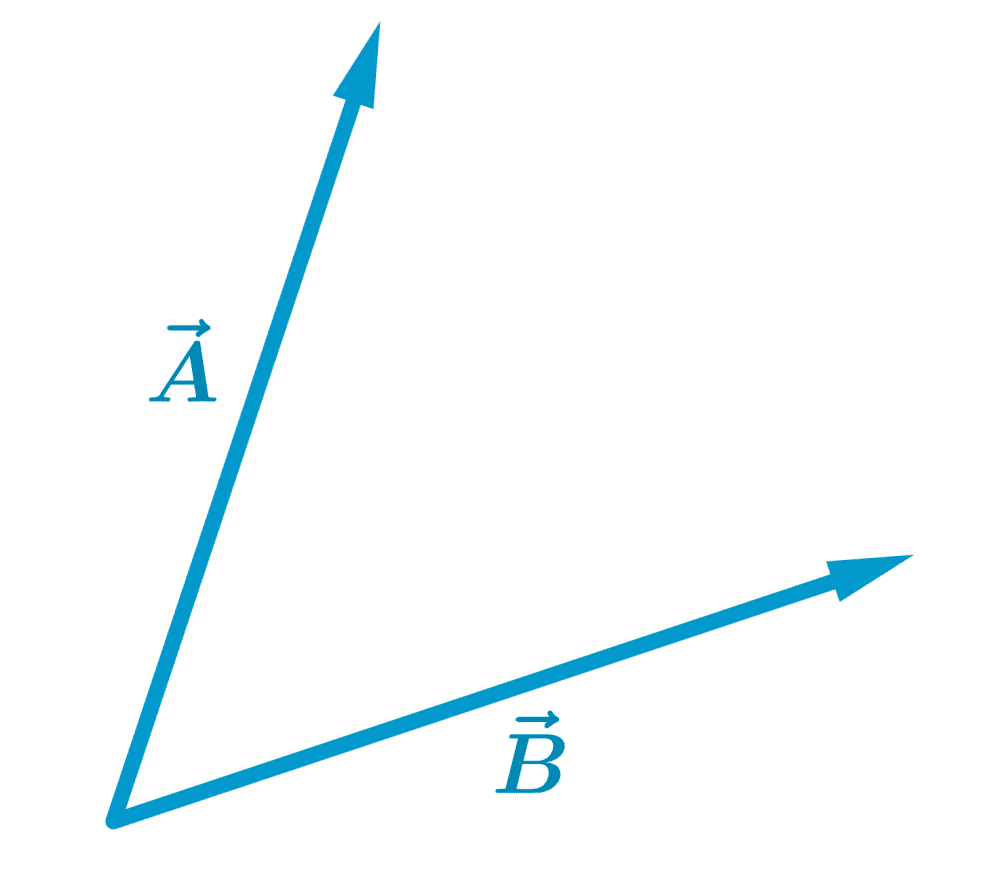
Luego, trazamos un paralelogramo usando a los vectores iniciales como lados adyacentes:
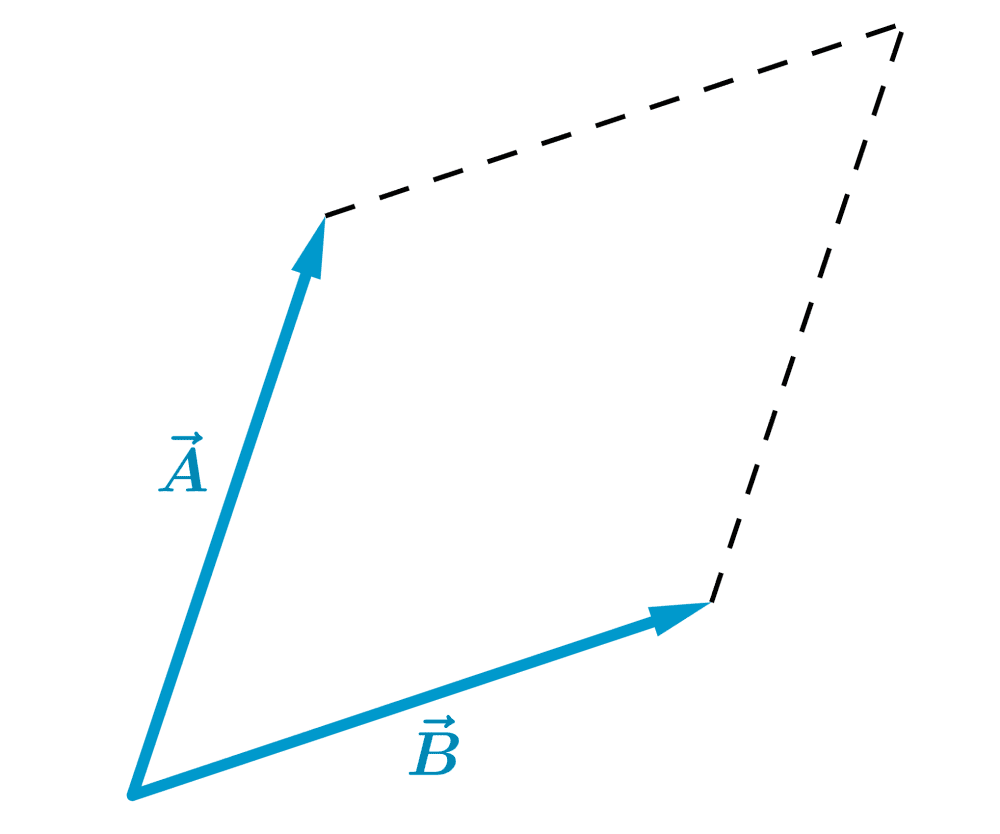
La diagonal del paralelogramo formado representa la suma de los vectores:
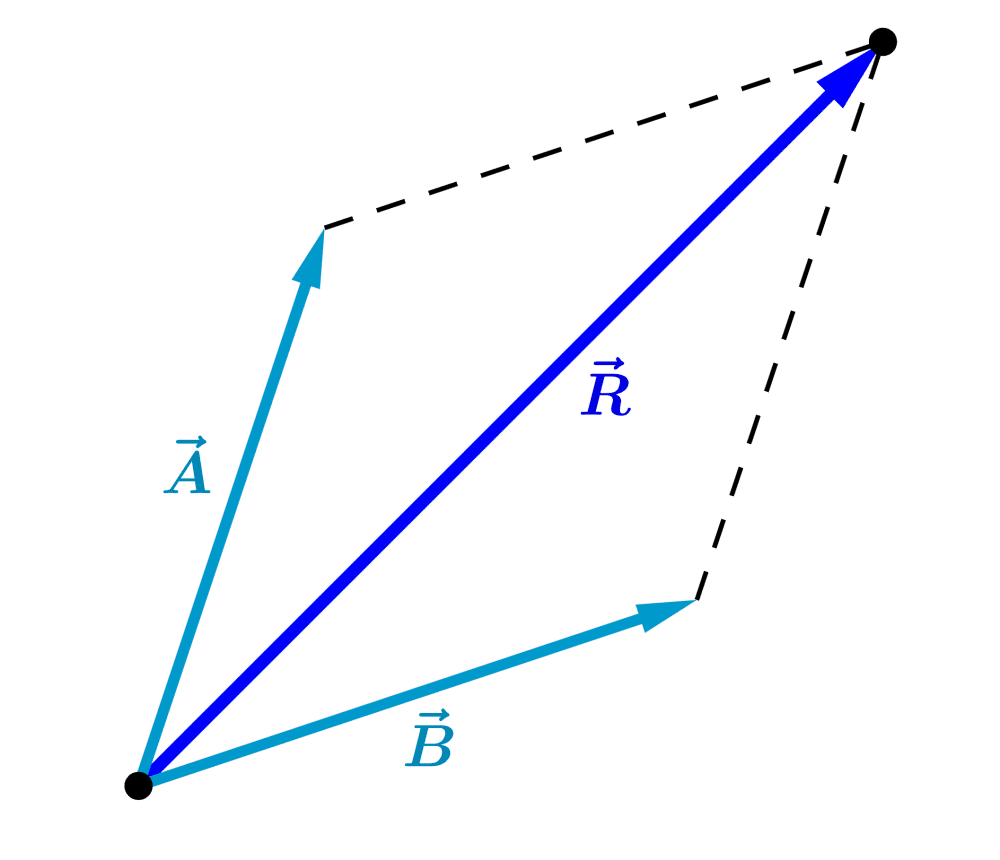
.
EJERCICIO 5
Encuentra la suma de los vectores usando el método del paralelogramo:
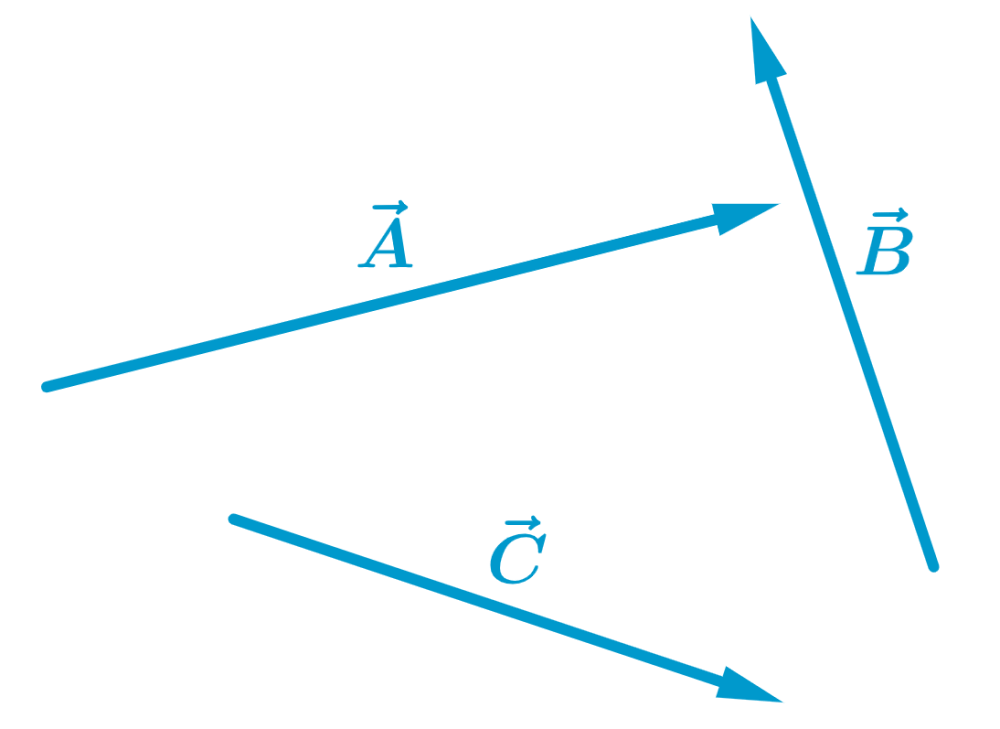
Solución
Empezamos sumando dos de los vectores para obtener el siguiente resultado:
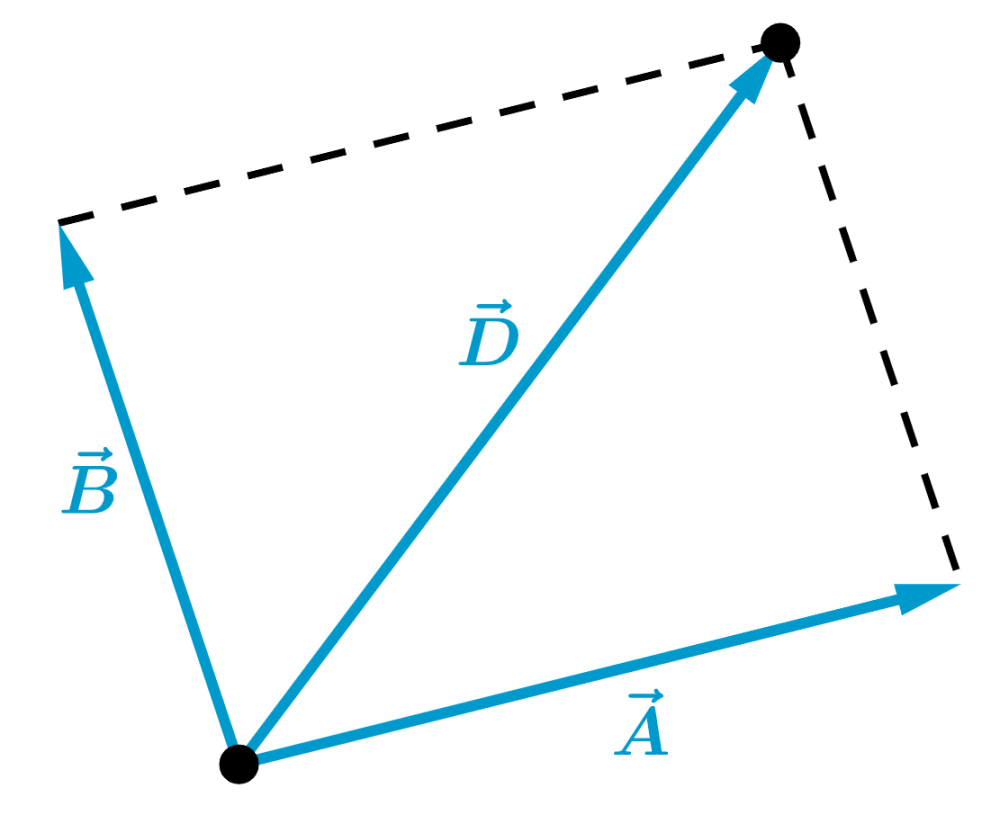
Ahora, sumamos al vector resultante con el tercer vector y tenemos:
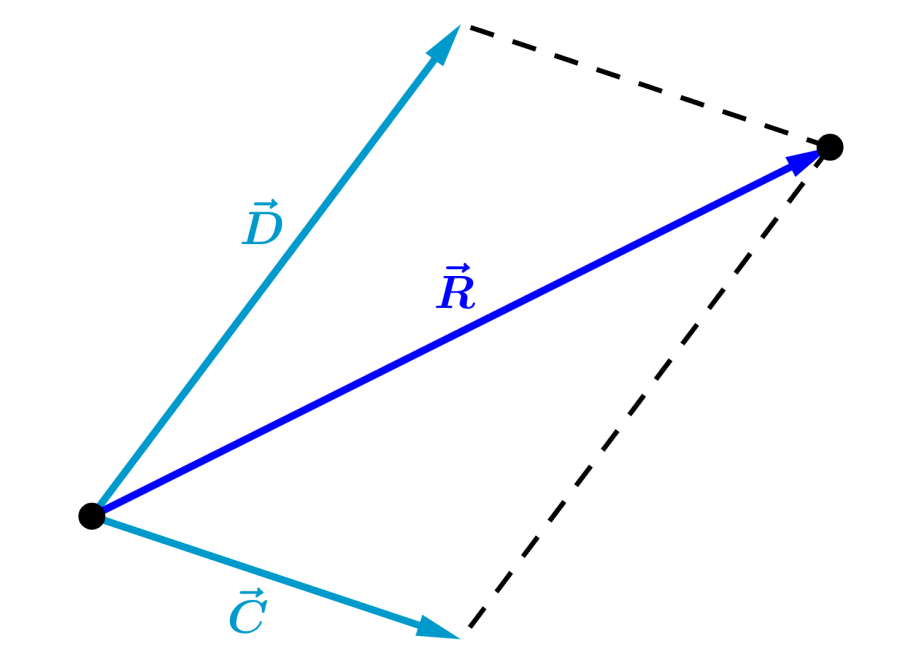
.
EJERCICIO 6
Suma los vectores $latex \vec{u}=2i+4j+5k$ y $latex \vec{v}=3i+j+2k$.
Solución
En este caso, tenemos los componentes de los vectores. En esta notación, las letras i, j, k representan a los componentes en x, y, z respectivamente.
Para sumar dos o más vectores, simplemente sumamos sus componentes para obtener el vector resultante $latex \vec{R}$. Entonces, tenemos:
$$R_{x}=u_{x}+v_{x}=2+3=5$$
$$R_{y}=u_{y}+v_{y}=4+1=5$$
$$R_{z}=u_{z}+v_{z}=5+2=7$$
Entonces, la suma de los vectores es
$latex \vec{R}=5i+5j+7k$
EJERCICIO 7
Suma los vectores $latex \vec{u}=-6i+8j+7k$ y $latex \vec{v}=3i-4j+5k$.
Solución
Similar al ejercicio anterior, simplemente tenemos que sumar los componentes de los vectores para encontrar su suma. Entonces, tenemos:
$$R_{x}=u_{x}+v_{x}=-6+3=-3$$
$$R_{y}=u_{y}+v_{y}=8-4=4$$
$$R_{z}=u_{z}+v_{z}=7+5=12$$
Entonces, la suma de los vectores es
$latex \vec{R}=-3i+4j+12k$
EJERCICIO 8
Encuentra la suma los vectores $latex \vec{u}=12i-9j+11k$, $latex \vec{v}=-5i-7j+7k$ y $latex \vec{w}=2i-3j+k$.
Solución
Para encontrar la suma de los vectores, vamos a sumar cada uno de sus componentes:
$$R_{x}=u_{x}+v_{x}+w_{x}=12-5+2=9$$
$$R_{y}=u_{y}+v_{y}+w_{y}=-9-7-3=-19$$
$$R_{z}=u_{z}+v_{z}+w_{z}=11+7+1=19$$
Entonces, el vector que representa a la suma de los vectores es
$latex \vec{R}=9i-19j+19k$
EJERCICIO 9
Encuentra el vector resultante al sumar los siguientes vectores:
$latex \vec{M}$: 20 m, 60 ° desde el este hacia el norte
$latex \vec{N}$: 10 m, 30 ° desde el este hacia el norte
Solución
Para encontrar la suma de los vectores, tenemos que empezar encontrando los componentes en $latex x$ y en $latex y$ de los dos vectores dados.
Podemos encontrar el componente $latex x$ usando el coseno y el componente $latex y$ usando el seno. Entonces, tenemos:
$$M_{x}=M\cos (\theta)=(20\text{ m})(\cos(60^{\circ})=10\text{ m}$$
$$M_{y}=M\sin (\theta)=(20\text{ m})(\sin(60^{\circ})=17.32\text{ m}$$
$$N_{x}=N\cos (\theta)=(10\text{ m})(\cos(30^{\circ})=8.66\text{ m}$$
$$N_{y}=N\sin (\theta)=(10\text{ m})(\sin(30^{\circ})=5\text{ m}$$
Ahora, solo sumamos los componentes:
$$R_{x}=M_{x}+N_{x}=10\text{ m}+8.66\text{ m}=18.66\text{ m}$$
$$R_{y}=M_{y}+N_{y}=17.32\text{ m}+5\text{ m}=22.32\text{ m}$$
Entonces, la suma de los vectores es $latex \vec{R}=18.66i+22.32j$.
EJERCICIO 10
¿Cuál es la suma de los siguientes vectores?
$latex \vec{A}$: 30 m, 45 ° desde el este hacia el norte
$latex \vec{B}$: 40 m, 30 ° desde el este hacia el norte
Solución
Tenemos que empezar encontrando los componentes en $latex x$ y en $latex y$. Entonces, tenemos:
$$A_{x}=A\cos (\theta)=(30\text{ m})(\cos(45^{\circ})=21.21\text{ m}$$
$$A_{y}=A\sin (\theta)=(30\text{ m})(\sin(45^{\circ})=21.21\text{ m}$$
$$B_{x}=B\cos (\theta)=(40\text{ m})(\cos(30^{\circ})=34.64\text{ m}$$
$$B_{y}=B\sin (\theta)=(40\text{ m})(\sin(30^{\circ})=20\text{ m}$$
Entonces, los componentes del vector formado por la suma son:
$$R_{x}=A_{x}+B_{x}=21.21\text{ m}+34.64\text{ m}=55.85\text{ m}$$
$$R_{y}=A_{y}+B_{y}=21.21\text{ m}+20\text{ m}=41.21\text{ m}$$
El vector resultante es $latex \vec{R}=55.85i+41.21j$.
Ejercicios de suma de vectores para resolver


Véase también
¿Interesado en aprender más sobre vectores? Puedes mirar estas páginas:


