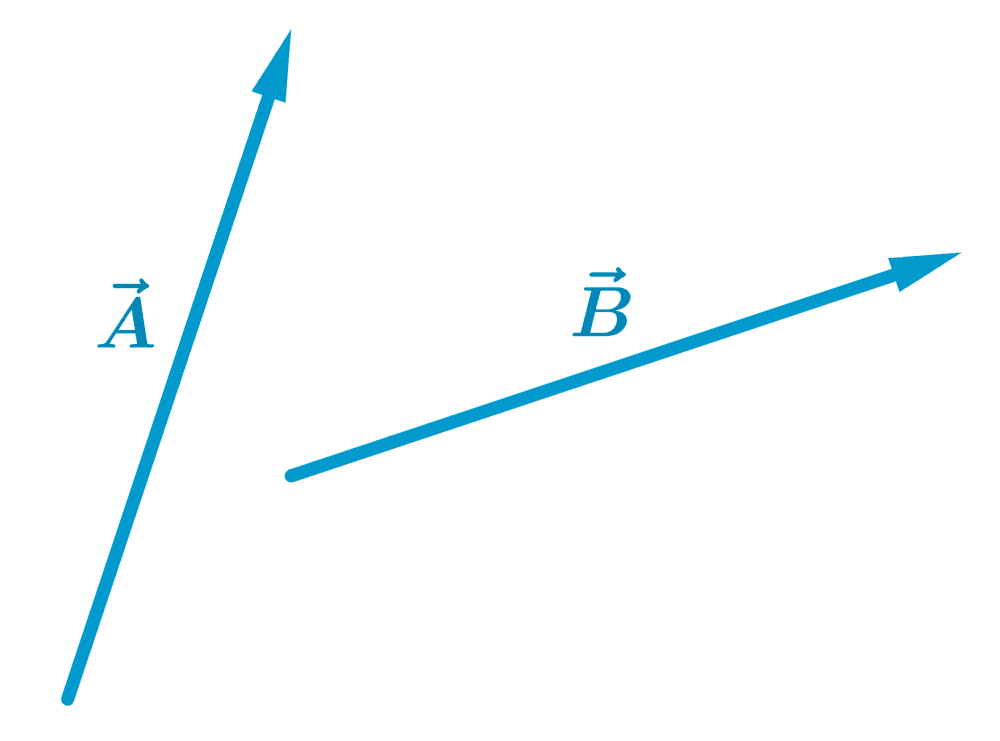Para sumar dos o más cantidades vectoriales, necesitamos un conjunto de operaciones diferentes a la aritmética ordinaria. Podemos usar tres métodos principales para sumar dos vectores: el método del polígono, el método del paralelogramo y el método de los componentes.
A continuación, conoceremos estos tres métodos para sumar vectores. Además, veremos algunos ejemplos para aplicar los conceptos.
Sumar vectores con el método del polígono
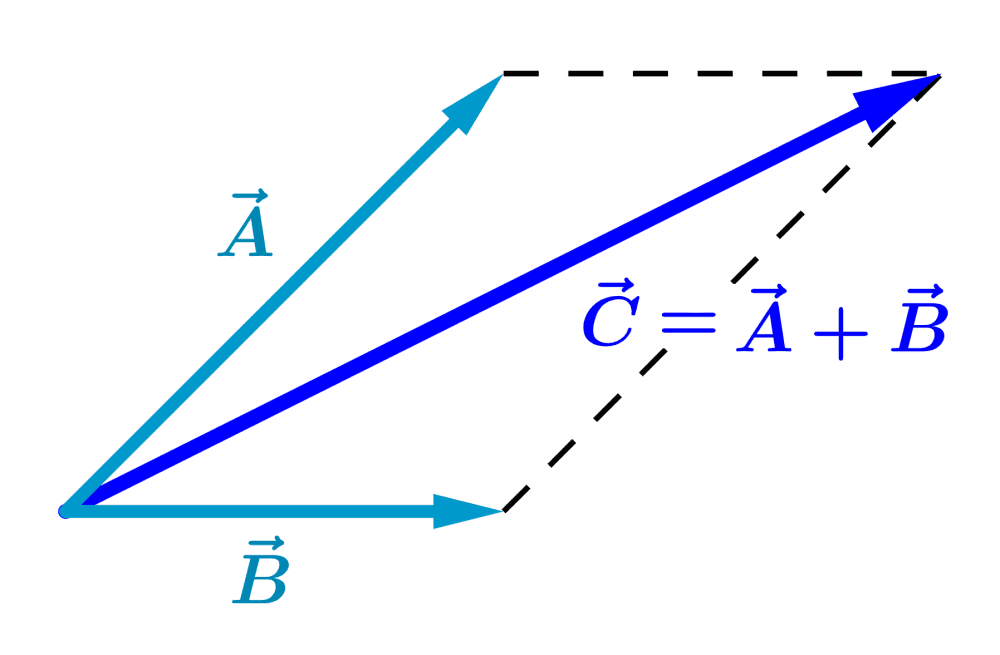
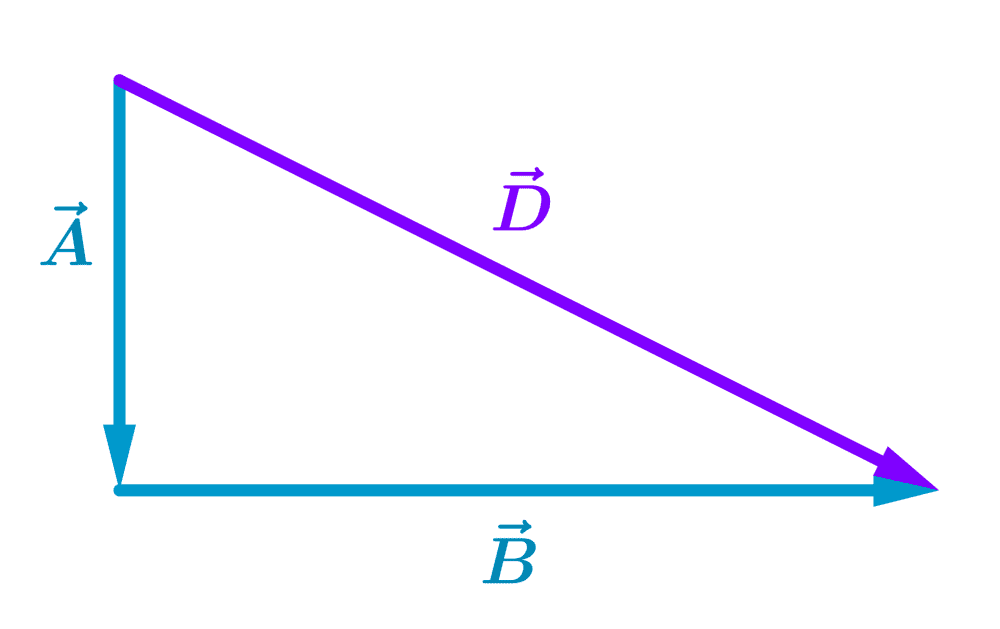
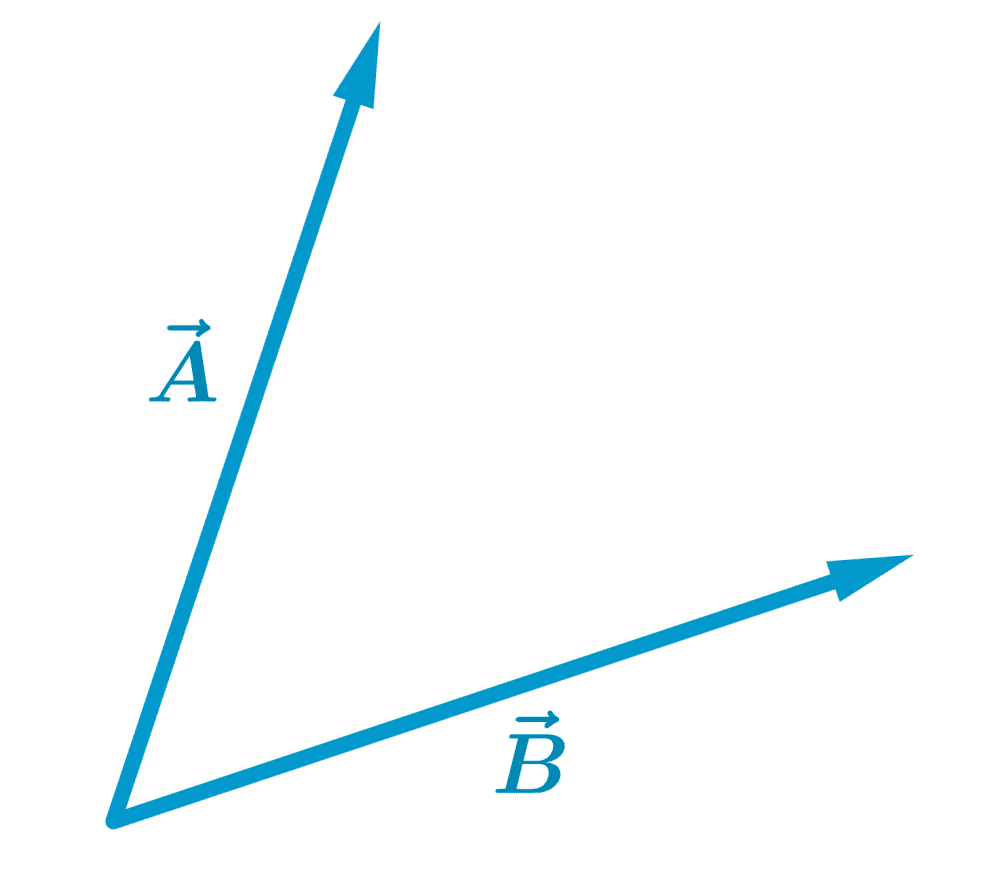
Supongamos que un objeto ha tenido un desplazamiento de $latex \vec{A}$ seguido por un segundo desplazamiento de $latex \vec{B}$, como se muestra en el siguiente diagrama:
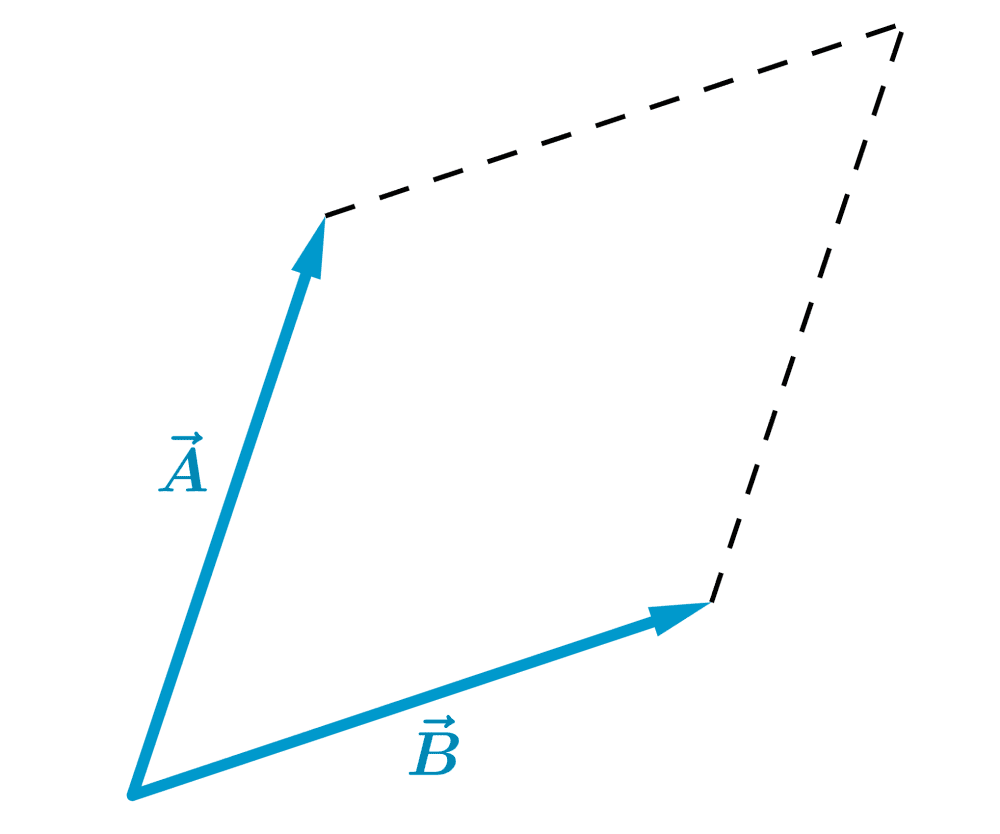
El resultado final es el mismo que si el objeto hubiera comenzado en el mismo punto inicial y realizado un solo desplazamiento $latex \vec{C}$.
El desplazamiento $latex \vec{C}$ es la suma de los vectores $latex \vec{A}$ y $latex \vec{B}$ y es expresado simbólicamente como:
$latex \vec{C}=\vec{A}+\vec{B}$
La suma de dos vectores no es la misma operación que sumar dos cantidades escalares como 3+5=8.
Para sumar dos vectores con el método del polígono, colocamos la cola o base del segundo vector en la cabeza o punta del primer vector.
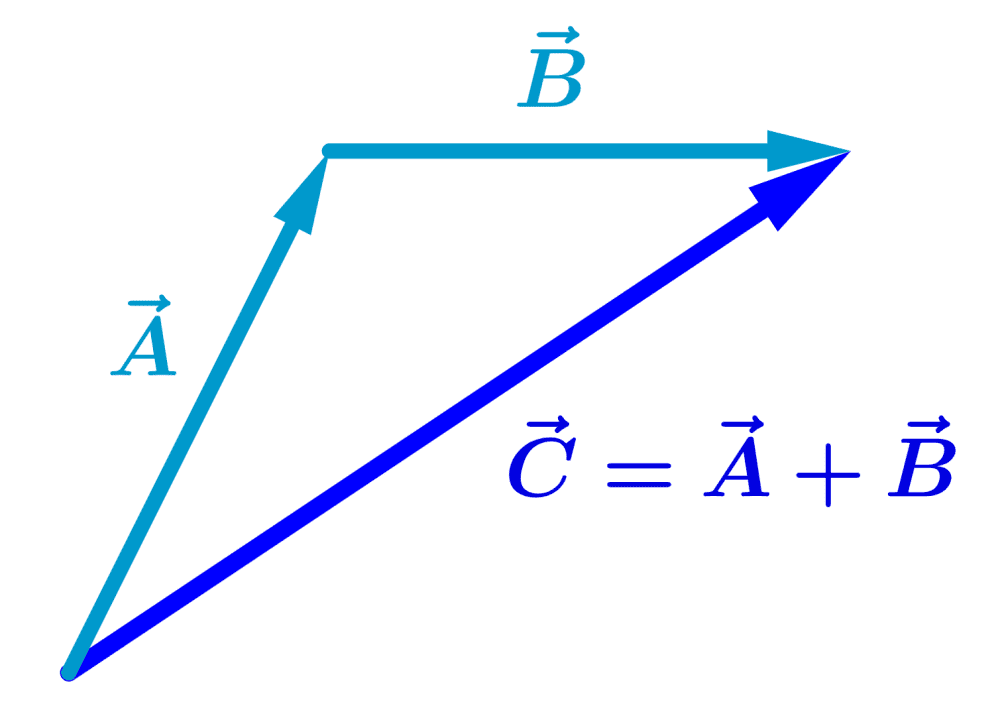
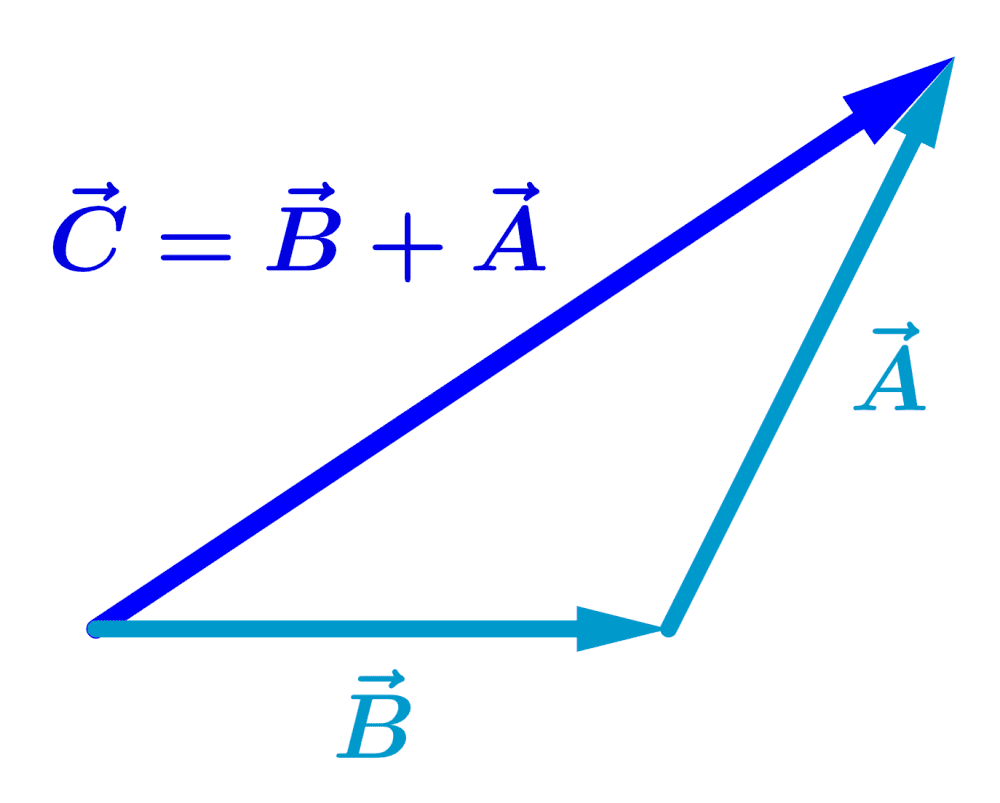
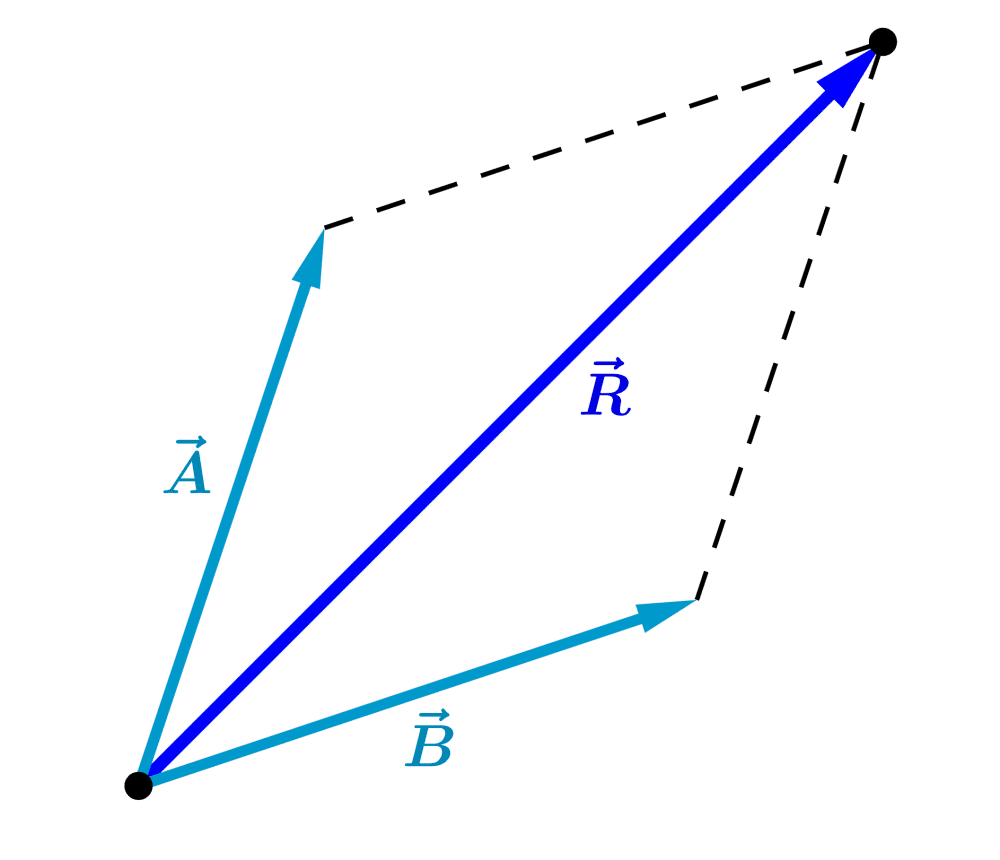
Si es que realizamos los desplazamientos $latex \vec{A}$ y $latex \vec{B}$ en orden reverso, es decir, $latex \vec{B}$ primero y $latex \vec{A}$ segundo, el resultado es el mismo:
Entonces, podemos observar que el orden de los términos en una suma de vectores no importa. Es decir, la propiedad conmutativa aplica en la suma de vectores
EJEMPLO 1
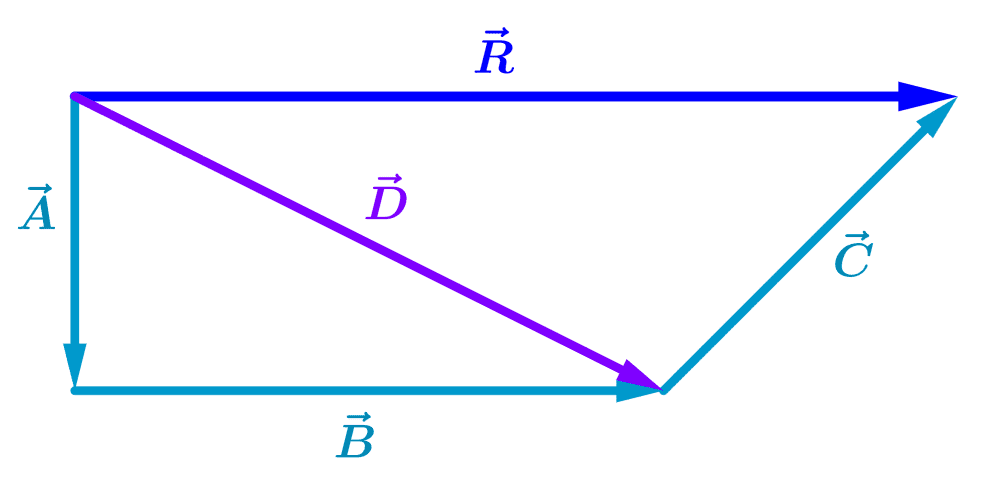
Encuentra la suma de los siguientes tres vectores:
Solución
Para encontrar la suma de los tres vectores, tenemos que empezar encontrando la suma de dos de los vectores y luego sumar el tercero.
Entonces, podemos empezar por sumar los vectores $latex \vec{A}$ y $latex \vec{B}$ para obtener el vector $latex \vec{D}$:
Luego, sumamos el vector $latex \vec{C}$ al vector $latex \vec{D}$ para obtener el resultado final $latex \vec{R}$:
Esta suma puede realizarse en cualquier otro orden. Por ejemplo, si sumamos $latex \vec{B}$ y $latex \vec{C}$ primero y $latex \vec{A}$ al final, obtendremos el mismo resultado.
EJEMPLO 2
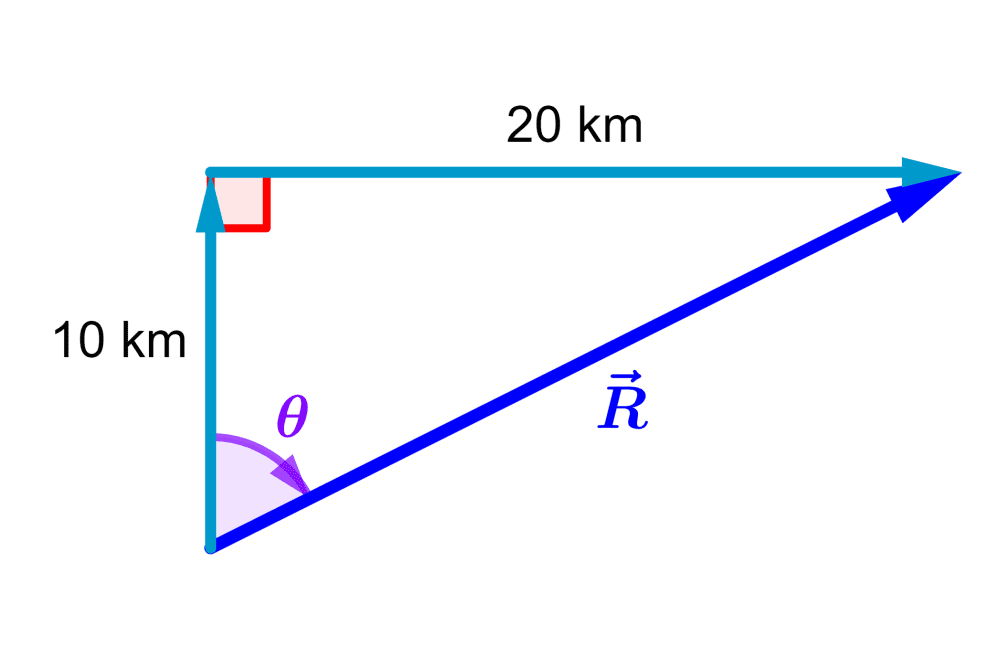
Un ciclista sale a dar un paseo 10 km hacia el norte y luego 20 km hacia el este. ¿Qué tan lejos y en qué dirección está del punto inicial?
Solución
Podemos empezar trazando un diagrama del problema. Usando el método de cabeza y cola, la suma de los vectores es:
Entonces, queremos encontrar la magnitud y la dirección (ángulo) del vector azul oscuro, el vector $latex \vec{R}$.
Dado que los vectores forman ángulos rectos el uno con el otro, el triángulo formado es un triángulo rectángulo. Entonces, podemos usar el teorema de Pitágoras y trigonometría.
La distancia desde el punto inicial hasta el punto final es igual a la longitud de la hipotenusa del triángulo:
$$\sqrt{(10\text{ km})^2+(20\text{ km})^2}=22.36\text{ km}$$
Podemos encontrar el ángulo θ usando la función tangente:
$$\tan(\theta)=\frac{\text{opuesto}}{\text{adyacente}}=\frac{20\text{ km}}{10\text{ km}}=2$$
$$\theta=\tan^{-1}(2)=63.4^{\circ}$$
Entonces, el ciclista está a 22.36 km en una dirección de 63.4° desde el norte hacia el este (eje x positivo).
Sumar vectores con el método del paralelogramo
El método del paralelogramo es otra forma de representar una suma de dos vectores gráficamente. Recordemos que un paralelogramo es un cuadrilátero en el cual sus lados opuestos son paralelos.
Supongamos que queremos representar la siguiente suma de vectores usando el método del paralelogramo:
$latex \vec{C}=\vec{A}+\vec{B}$
Podemos dibujar a los vectores $latex \vec{A}$ y $latex \vec{B}$ con sus colas o bases en el mismo punto. Luego, construimos un paralelogramo, en donde, $latex \vec{A}$ y $latex \vec{B}$ son dos lados adyacentes:
Entonces, el resultado de la suma, es decir, el vector $latex \vec{C}$ es la diagonal del paralelogramo construido.
EJEMPLO
Encuentra la suma de los siguientes vectores usando el método del paralelogramo.
Solución
Para encontrar el vector resultante, tenemos que colocar a los vectores con sus bases en el mismo punto. Entonces, tenemos:
Luego, formamos un paralelogramo en el cual los vectores iniciales son sus lados adyacentes:
La suma de los vectores es igual a la diagonal del paralelogramo formado:
.
Sumar vectores usando sus componentes
Dos o más vectores pueden ser sumados fácilmente si es que conocemos sus componentes. Para esto, solo tenemos que sumar sus componentes $latex x$ y $latex y$ separadamente.
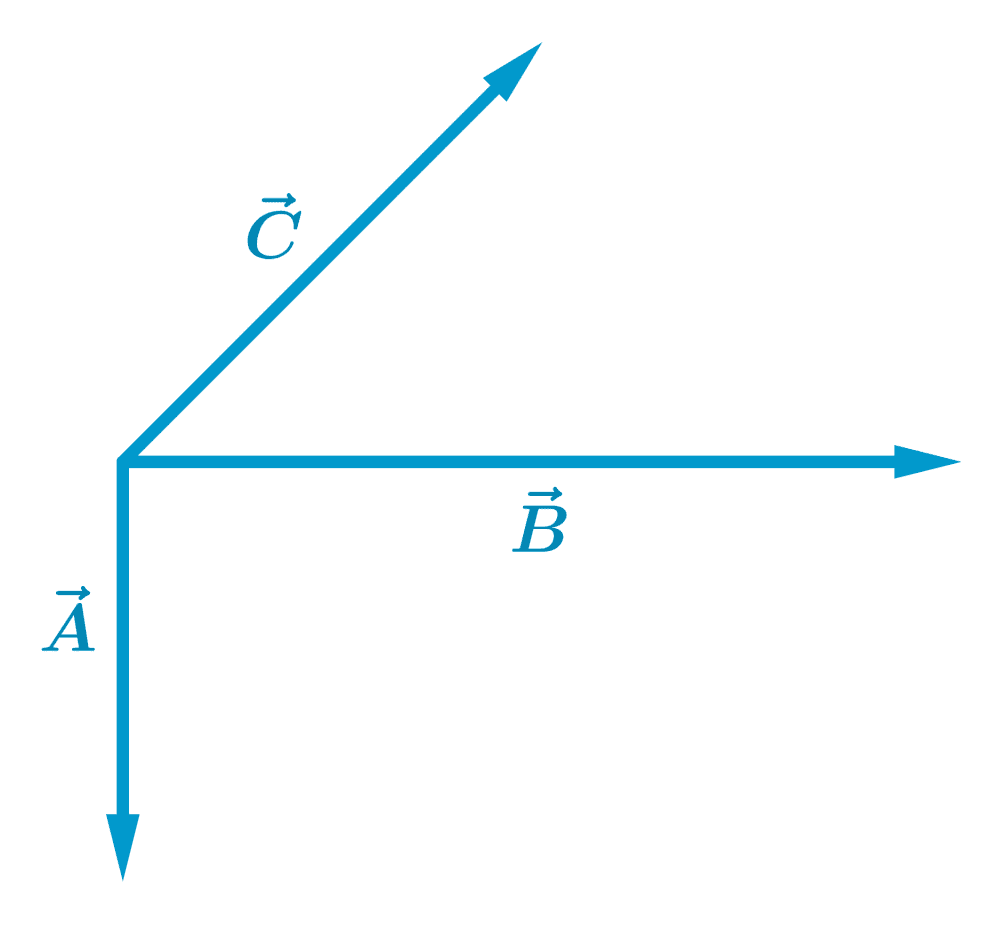
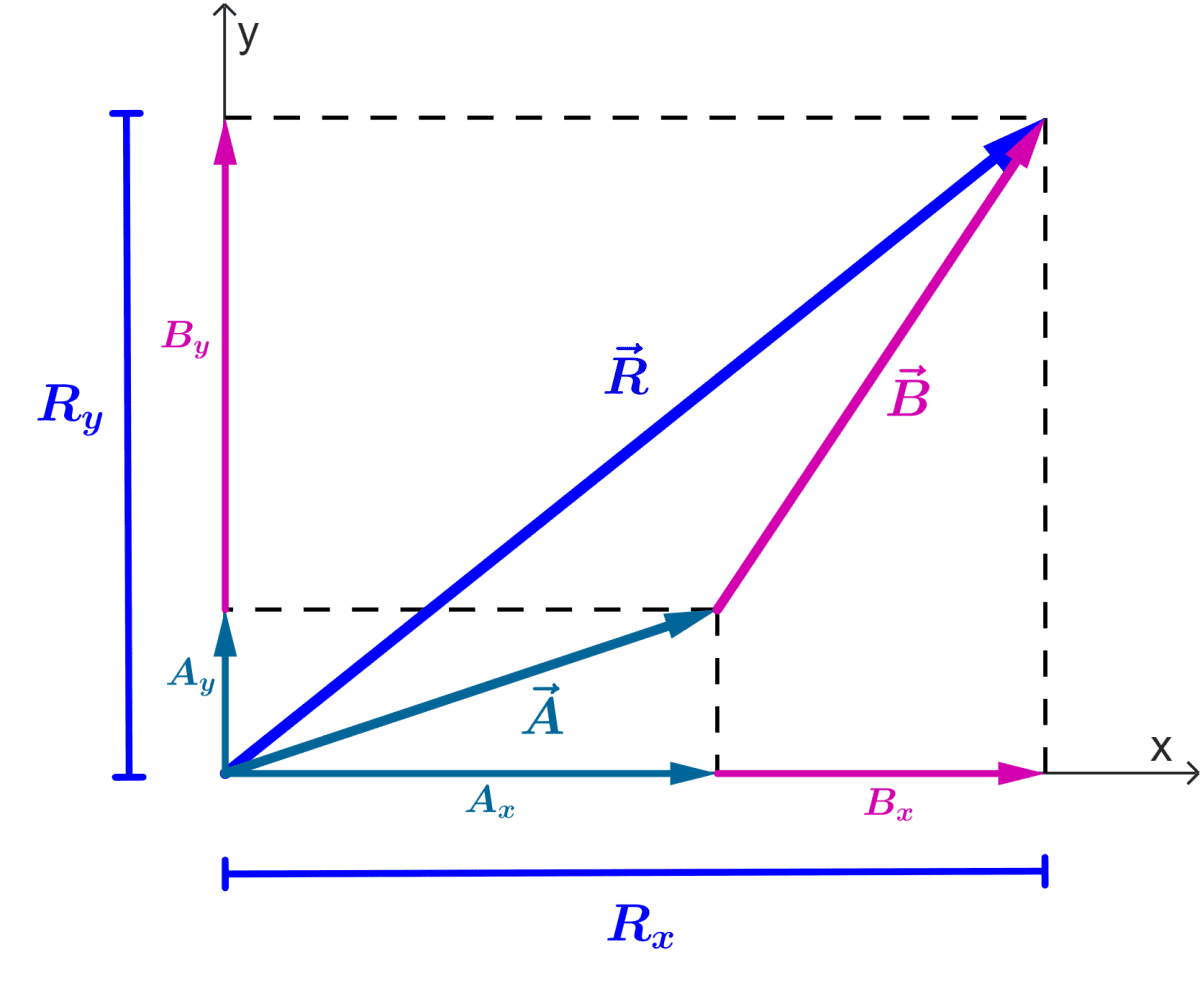
Supongamos que tenemos dos vectores $latex \vec{A}$ y $latex \vec{B}$ y queremos encontrar el vector $latex \vec{C}$, el cual es la suma de los dos vectores.
Podemos usar el siguiente diagrama para visualizar esto:
Podemos observar que el componente $latex x$ de $latex \vec{C}$ es igual a la suma de los componentes $latex x$ de los vectores ($latex A_{x}+B_{x}$).
Lo mismo aplica para los componentes $latex y$. Entonces, tenemos:
$latex C_{x}=A_{x}+B_{x}$
$latex C_{y}=A_{y}+B_{y}$
Podemos usar este método para encontrar la suma de cualquier número de vectores en 2D o 3D. Por ejemplo, si es que $latex \vec{D}$ es la suma de $latex \vec{A}, \vec{B}, \vec{C}$, tenemos
$latex D_{x}=A_{x}+B_{x}+C_{x}$
$latex D_{y}=A_{y}+B_{y}+C_{y}$
EJEMPLO 1
Encuentra la suma de los vectores $latex \vec{u}=3i+2j+5k$ y $latex \vec{v}=2i+j+3k$.
Solución
En esta notación, las letras i, j, k representan a los componentes en x, y, z respectivamente.
Entonces, para encontrar los componentes del vector formado por la suma de $latex \vec{u}$ y $latex \vec{v}$, sumamos los componentes de los vectores:
$$R_{x}=u_{x}+v_{x}=3+2=5$$
$$R_{y}=u_{y}+v_{y}=2+1=3$$
$$R_{z}=u_{z}+v_{z}=5+3=8$$
Entonces, la suma de los vectores es
$latex \vec{R}=5i+3j+8k$
EJEMPLO 2
Encuentra los componentes del vector formado por la suma de los siguientes vectores:
$latex \vec{A}$: 20 m, 60 ° desde el este hacia el norte
$latex \vec{B}$: 10 m, 30 ° desde el este hacia el norte
Solución
Para resolver este problema, tenemos que empezar encontrando los componentes en $latex x$ y en $latex y$ de los dos vectores dados.
Entonces, usamos las fórmulas de los componentes de un vector, recordando que encontramos el componente $latex x$ con el coseno y el componente $latex y$ con el seno:
$$A_{x}=A\cos (\theta)=(20\text{ m})(\cos(60^{\circ})=10\text{ m}$$
$$A_{y}=A\sin (\theta)=(20\text{ m})(\sin(60^{\circ})=17.32\text{ m}$$
$$B_{x}=B\cos (\theta)=(10\text{ m})(\cos(30^{\circ})=8.66\text{ m}$$
$$B_{y}=B\sin (\theta)=(10\text{ m})(\sin(30^{\circ})=5\text{ m}$$
Entonces, los componentes del vector formado por la suma son:
$$R_{x}=A_{x}+B_{x}=10\text{ m}+8.66\text{ m}=18.66\text{ m}$$
$$R_{y}=A_{y}+B_{y}=17.32\text{ m}+5\text{ m}=22.32\text{ m}$$
Véase también
¿Interesado en aprender más sobre vectores? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
