Calculadora de Arccsc (Cosecante inversa)
csc-1() =
Grados:
Radianes:
π radianes:
Gráfica de la cosecante inversa
El dominio de x es x≤-1 y x≥1.
El rango es -π/2≤y<0 o 0<y≤π/2.
Usa esta calculadora para obtener el resultado de la cosecante inversa de un valor ingresado. Podrás obtener la solución en grados, radianes y π radianes. El dominio permitido de x es x≤-1 y x≥1.
A continuación, puedes encontrar información adicional sobre cómo usar la calculadora de cosecante inversa. Además, podrás explorar la definición, la gráfica y valores importantes de la cosecante.
¿Cómo usar la calculadora de cosecante inversa?
Paso 1: Ingresa el valor de x en la primera casilla. El valor ingresado debe estar en el dominio x≤-1 y x≥1
Paso 2: El resultado será mostrado en grados en el panel derecho.
Paso 3: La solución en radianes y π radianes será mostrada en la parte inferior.
Diferencia entre grados, radianes y π radianes
La relación entre grados y radianes puede ser encontrada considerando que tenemos 360° y 2π radianes en una revolución completa. Entonces, podemos deducir que 180° es igual a π radianes.
Por otra parte, podemos conocer la diferencia entre «radianes» y «π radianes» al recordar que π tiene un valor aproximado de 3.1415… Entonces, 0.5 π radianes es equivalente a 1.571 radianes ya que el valor de π es incluido en el segundo caso.
¿Qué es la cosecante inversa?
La cosecante inversa, también conocida como arco cosecante, es la función inversa de la cosecante. Esto significa que la cosecante inversa revierte el efecto producido por la función cosecante.
Por ejemplo, la cosecante de 30° es igual a 2. Entonces, la cosecante inversa de 2 es igual a 30°.
La función cosecante inversa puede ser denotada como csc-1(x) o también como arccsc(x). Considerando que la función cosecante y la función seno son recíprocas, csc-1(x) es equivalente a sen-1(1/x).
Podemos usar la cosecante inversa para encontrar los ángulos en un triángulo rectángulo si es que conocemos las proporciones o las longitudes de sus lados. Poe ejemplo, podemos encontrar el ángulo A del siguiente triángulo usando arccsc(x), en donde, x es igual a c/a.
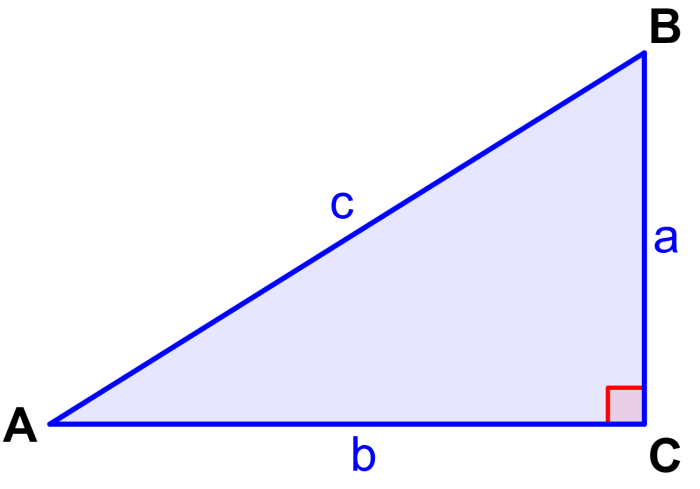
¿Por qué no podemos usar valores de x entre -1 y 1 en la cosecante inversa?
Dado que la cosecante inversa es la función inversa de la cosecante, sus dominios y rangos están intercambiados. Esto significa que el rango de la cosecante es igual al dominio de la cosecante inversa.
Además, no hay ningún valor de x que haga que los valores de y en la cosecante estén entre -1 y 1. Por lo tanto, los valores de x de la cosecante inversa no pueden estar entre -1 y 1.
Gráfica de la cosecante inversa
Podemos graficar a la cosecante inversa si es que consideramos un rango fijo. En esta calculadora, tomamos un rango que va desde -π/2 hasta π/2 y no incluye al 0 como se muestra a continuación:
Dominio de la cosecante inversa
De la gráfica de la cosecante inversa, podemos deducir que los valores de x pueden ser cualquier valor real, excluyendo a los valores entre -1 y 1. Entonces, el dominio de la cosecante inversa es igual a x≤-1 y x≥1.
Rango de la cosecante inversa
De la gráfica de la cosecante inversa, podemos deducir que los valores de y de la función van desde -π/2 hasta π/2 sin incluir al 0. Entonces, su rango es -π/2≤y< 0 o 0<y≤π/2.
Tabla de valores de cosecante inversa importantes
| Valor de x | arccsc(x)(°) | arccsc(x)(rad) |
| 1 | 90° | |
| 60° | ||
| 45° | ||
| 30° | ||
| -1 | -90° | – |
Calculadoras relacionadas:
- Calculadora de Arccos (Coseno inverso) – Grados y Radianes
- Calculadora de Arcsin (Seno inverso) – Grados y Radianes
- Calculadora de Arctan (Tangente inversa) – Grados y Radianes
- Calculadora de Arcsec(Secante inversa) – Grados y Radianes
- Calculadora de Arccot (Cotangente inversa) – Grados y Radianes
Puedes encontrar más calculadoras aquí.
