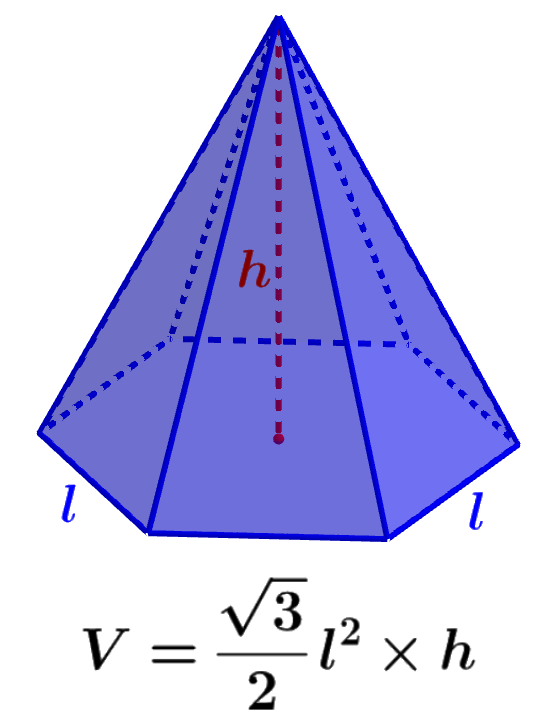
El volumen de una pirámide hexagonal es encontrado al multiplicar al área de la base hexagonal por la altura de la pirámide y dividir por tres. Para calcular el área superficial, tenemos que sumar las áreas de todas las caras de la pirámide.
A continuación, conoceremos las fórmulas que podemos usar para calcular el volumen y el área superficial de pirámides hexagonales. Luego, aplicaremos esta fórmula para resolver algunos ejercicios de práctica.
GEOMETRÍA
Relevante para…
Aprender a calcular el volumen y área de una pirámide hexagonal.
GEOMETRÍA
Relevante para…
Aprender a calcular el volumen y área de una pirámide hexagonal.
¿Cómo calcular el volumen de una pirámide hexagonal?
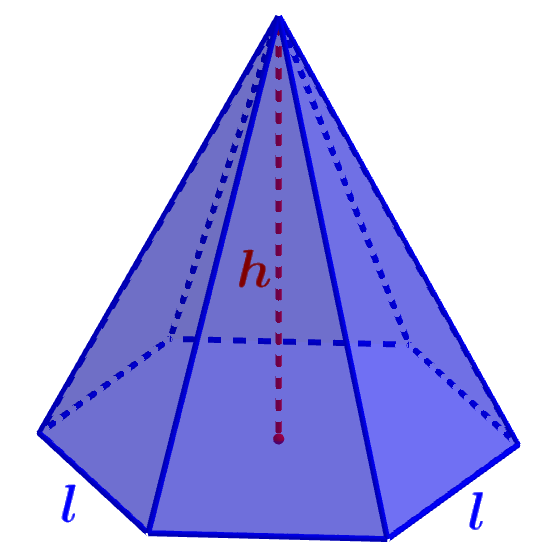
Una pirámide es una figura tridimensional que está compuesta de una base y de caras laterales que se encuentran en un punto único superior. El volumen de estas figuras es encontrado al multiplicar el área de su base por su altura y dividir por tres. Entonces, tenemos la siguiente fórmula:
$latex \text{Volumen} = \frac{1}{3}\text{Base} \times \text{Altura}$
Las pirámides hexagonales tienen a un hexágono como su base, por lo que tenemos que encontrar una expresión para el área de un hexágono. El área de un hexágono es calculada usando su apotema y la longitud de uno de sus lados.
Sin embargo, también es posible encontrar el área de hexágonos simplemente usando la longitud de uno de sus lados. Para esto, usamos la siguiente fórmula:
$latex A= \frac{3\sqrt{3}}{2}{{l}^2}$
en donde, l representa a la longitud de uno de los lados del hexágono.
Si es que sustituimos a esta expresión en la fórmula del volumen de una pirámide, tenemos:
$latex V=\frac{1}{3}\times \frac{3\sqrt{3}}{2}{{l}^2}\times h$
| $latex V=\frac{\sqrt{3}}{2}{{l}^2}\times h$ |
en donde, l es la longitud de uno de los lados de la base hexagonal y h es la longitud de la altura de la pirámide.
¿Cómo encontrar el área superficial de una pirámide hexagonal?
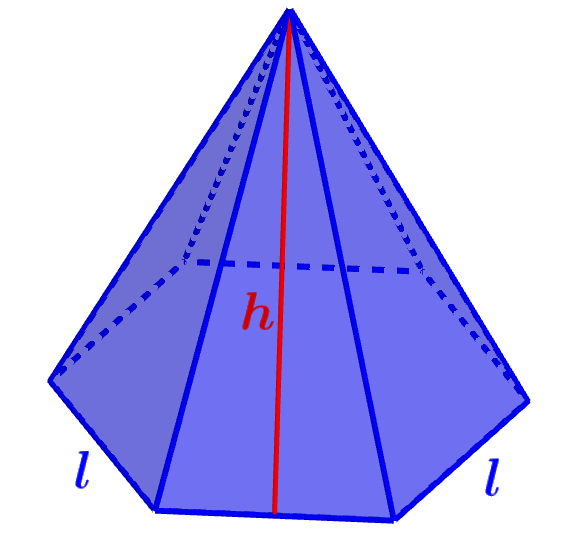
El área superficial es encontrada al sumar las áreas de todas las caras de la figura tridimensional. Estas pirámides tienen una cara hexagonal y seis caras triangulares laterales.
El área de la base hexagonal es encontrada usando la fórmula del área de un hexágono:
$latex A=\frac{3\sqrt{3}}{2}{{l}^2}$
en donde, l representa a la longitud de uno de los lados del hexágono.
Por otra parte, el área de las caras triangulares es encontrada usando la fórmula del área de cualquier triángulo:
$latex A=\frac{1}{2}b\times h$
en donde, b es la longitud de la base del triángulo y h es la longitud de la altura del triángulo.
En una pirámide hexagonal, la base de las caras triangulares es igual a los lados de la base hexagonal. Además, considerando que las seis caras triangulares son iguales, tenemos la siguiente fórmula del área superficial de pirámides hexagonales:
$latex A_{s}=\frac{3\sqrt{3}}{2}{{l}^2}+6(\frac{1}{2}b\times h)$
$latex A_{s}=\frac{3\sqrt{3}}{2}{{l}^2}+3lh)$
Ejercicios de volumen y área de pirámides hexagonales resueltos
EJERCICIO 1
Si es que una pirámide tiene una altura de 4 m y una base hexagonal con lados de 1 m, ¿cuál es su volumen?
Solución
Tenemos la siguiente información:
- Altura, $latex h=4$
- Lados de hexágono, $latex l=1$
Tenemos que usar estos valores en la fórmula del volumen:
$latex V=\frac{\sqrt{3}}{2}{{l}^2}\times h$
$latex V=\frac{\sqrt{3}}{2}{{(1)}^2}\times (4)$
$latex V=\frac{\sqrt{3}}{2}(4)$
$latex V=3.46$
El volumen es igual a 3.46 m³.
EJERCICIO 2
Si es que una pirámide tiene una base hexagonal con lados de longitud de 1 m y sus caras triangulares tienen una altura de 3 m, ¿cuál es su área superficial?
Solución
Tenemos las longitudes $latex l=1$ y $latex h=3$. Entonces, usamos la fórmula del área superficial con estos valores:
$latex A_{s}=\frac{3\sqrt{3}}{2}{{l}^2}+3lh$
$latex A_{s}=\frac{3\sqrt{3}}{2}{{(1)}^2}+3(1)(3)$
$latex A_{s}=\frac{3\sqrt{3}}{2}(1)+9$
$latex A_{s}=2.6+9$
$latex A_{s}=11.6$
El área superficial es igual a 11.6 m².
EJERCICIO 3
¿Cuál es el volumen de una pirámide que tiene una altura de 5 m y una base hexagonal con lados de 2 m?
Solución
Tenemos los siguientes datos:
- Altura, $latex h=5$
- Lados de hexágono, $latex l=2$
Usamos la fórmula del volumen con estos datos:
$latex V=\frac{\sqrt{3}}{2}{{l}^2}\times h$
$latex V=\frac{\sqrt{3}}{2}{{(2)}^2}\times (5)$
$latex V=\frac{\sqrt{3}}{2}(20)$
$latex V=17.32$
El volumen es igual a 17.32 m³.
EJERCICIO 4
Si es que una pirámide tiene una base hexagonal con lados de 2 m y caras triangulares de altura de 5 m, ¿cuál es su área superficial?
Solución
Tenemos los valores $latex l=2$ y $latex h=5$. Al usar estos valores en la fórmula del área superficial, tenemos:
$latex A_{s}=\frac{3\sqrt{3}}{2}{{l}^2}+3lh$
$latex A_{s}=\frac{3\sqrt{3}}{2}{{(2)}^2}+3(2)(5)$
$latex A_{s}=\frac{3\sqrt{3}}{2}(4)+30$
$latex A_{s}=10.4+30$
$latex A_{s}=40.4$
El área superficial es igual a 40.4 m².
EJERCICIO 5
Si es que una pirámide hexagonal tiene lados de longitud 3 m y una altura de 8 m, ¿cuál es su volumen?
Solución
Tenemos lo siguiente:
- Altura, $latex h=8$
- Lados de hexágono, $latex l=3$
Al usar la fórmula del volumen con estos datos, tenemos:
$latex V=\frac{\sqrt{3}}{2}{{l}^2}\times h$
$latex V=\frac{\sqrt{3}}{2}{{(3)}^2}\times (8)$
$latex V=\frac{\sqrt{3}}{2}(72)$
$latex V=62.35$
El volumen es igual a 62.35 m³.
EJERCICIO 6
¿Cuál es el área superficial de una pirámide hexagonal con lados de 4 m y caras triangulares de altura de 6 m?
Solución
En la pregunta, tenemos las longitudes $latex l=4$ y $latex h=6$. Usando estos valores en la fórmula, tenemos:
$latex A_{s}=\frac{3\sqrt{3}}{2}{{l}^2}+3lh$
$latex A_{s}=\frac{3\sqrt{3}}{2}{{(4)}^2}+3(4)(6)$
$latex A_{s}=\frac{3\sqrt{3}}{2}(16)+72$
$latex A_{s}=41.6+72$
$latex A_{s}=113.6$
El área superficial es igual a 113.6 m².
EJERCICIO 7
¿Cuál es la altura de una pirámide que tiene un volumen de 50 m³ y una base hexagonal con lados de longitud 3 m?
Solución
Tenemos la siguiente información:
- Volumen, $latex V=50$
- Lados de hexágono, $latex l=3$
Aquí, tenemos la medida del volumen, pero tenemos que encontrar la longitud de la altura. Entonces, usamos la fórmula del volumen y resolvemos para h:
$latex V=\frac{\sqrt{3}}{2}{{l}^2}\times h$
$latex 50=\frac{\sqrt{3}}{2}{{(3)}^2}\times h$
$latex 50=\frac{\sqrt{3}}{2}(9)\times h$
$latex 50=7.79 h$
$latex h\approx 6.42$
La longitud de la altura es igual a 6.42 m.
EJERCICIO 8
Si es que una pirámide tiene una base hexagonal con lados de longitud de 5 m y sus caras triangulares tienen una altura de 10 m, ¿cuál es su área superficial?
Solución
Tenemos las longitudes $latex l=5$ y $latex h=10$. Entonces, usamos la fórmula del área superficial con estos valores:
$latex A_{s}=\frac{3\sqrt{3}}{2}{{l}^2}+3lh$
$latex A_{s}=\frac{3\sqrt{3}}{2}{{(5)}^2}+3(5)(10)$
$latex A_{s}=\frac{3\sqrt{3}}{2}(25)+150$
$latex A_{s}=65+150$
$latex A_{s}=215$
El área superficial es igual a 215 m².
EJERCICIO 9
Si es que una pirámide tiene un volumen de 64 m³ y una base hexagonal con lados de 4 m, ¿cuál es la longitud de su altura?
Solución
Tenemos lo siguiente:
- Volumen, $latex V=64$
- Lados de hexágono, $latex l=4$
Similar al ejercicio anterior, usamos la fórmula del volumen y resolvemos para h:
$latex V=\frac{\sqrt{3}}{2}{{l}^2}\times h$
$latex 64=\frac{\sqrt{3}}{2}{{(4)}^2}\times h$
$latex 64=\frac{\sqrt{3}}{2}(16)\times h$
$latex 64=13.86 h$
$latex h\approx 4.62$
La longitud de la altura es igual a 4.62 m.
Ejercicios de volumen y área de pirámides hexagonales para resolver
¿Cuál es la altura de una pirámide que tiene un volumen de 79.5 m3 y una base hexagonal con lados de 3 m?
Escribe la respuesta usando un solo lugar decimal.
Véase también
¿Interesado en aprender más sobre pirámides? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
