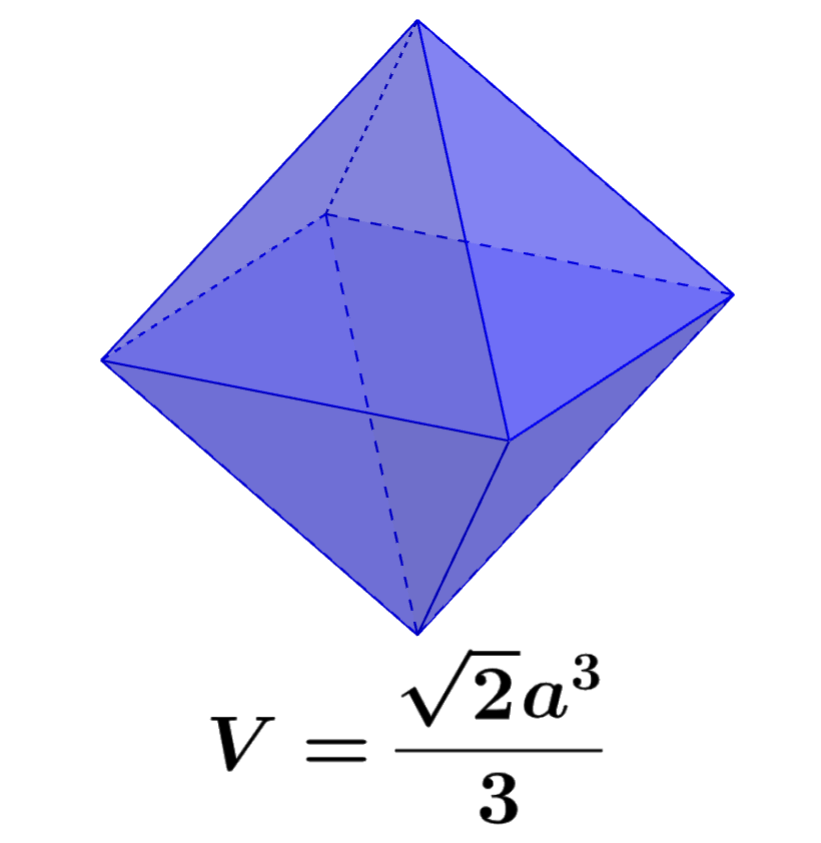Un octaedro es una figura tridimensional formada al unir a dos pirámides en sus bases. Podemos calcular el volumen de un octaedro al sumar el volumen de las dos pirámides que lo componen. Además, el área superficial es calculada al sumar las áreas de sus ocho caras.
A continuación, conoceremos las fórmulas que podemos usar para calcular el volumen y el área de un octaedro. Aprenderemos a derivar estas fórmulas y las aplicaremos para resolver algunos ejercicios.
Cómo encontrar el volumen de un octaedro
Podemos calcular el volumen de un octaedro usando la siguiente fórmula:
| $latex V=\frac{\sqrt{2}}{3} {{a}^3}$ |
en donde, a es la longitud de uno de los lados del octaedro.
Demostración de la fórmula del volumen de un octaedro
Un octaedro puede ser formado al unir a dos pirámides en sus bases. Esto significa que podemos obtener el volumen de un octaedro si es que sumamos los volúmenes de ambas pirámides.
Dado que ambas pirámides son iguales, esto significa que tenemos que encontrar el volumen de una pirámide y simplemente multiplicar por 2 para obtener el volumen del octaedro.
Ahora, para calcular el volumen de cualquier pirámide, podemos usar la siguiente fórmula:
$latex V_{p}=\frac{A_{b}\times h}{3}$
en donde, $latex A_{b}$ es el área de la base y h es la altura de la pirámide.
En este caso, la base de la pirámide es cuadrada, por lo que su área es igual a $latex {{a}^2}$.
La altura de la pirámide puede ser calculada usando el teorema de Pitágoras usando el siguiente diagrama:
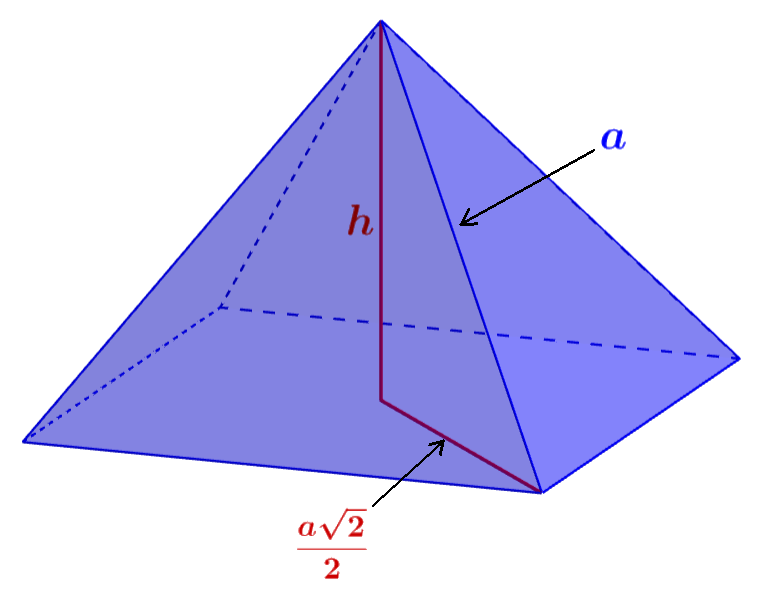
Dado que las caras de un octaedro son triángulos equiláteros, todos sus lados tienen longitud a. Entonces, la hipotenusa que usaremos es igual a a.
Además, dado que la diagonal de un cuadrado es igual a $latex a\sqrt{2}$, la mitad de la diagonal, que es igual a uno de los catetos, es igual a $latex \frac{a\sqrt{2}}{2}$.
Entonces, la altura de la pirámide es:
$latex h=\sqrt{{{a}^2}-{{(\frac{a\sqrt{2}}{2})}^2}}$
$latex h=\sqrt{{{a}^2}-\frac{{{a}^2}}{2}}$
$latex h=\sqrt{\frac{{{a}^2}}{2}}$
$latex h=\frac{a}{\sqrt{2}}$
$latex h=\frac{a \sqrt{2}}{2}$
Multiplicando la altura por el área de la base y dividiendo por 3, obtenemos el volumen de la pirámide:
$latex V_{p}=\frac{1}{3}\times{{a}^2}\times \frac{a \sqrt{2}}{2}$
$latex V_{p}=\frac{{{a}^3} \sqrt{2}}{6}$
Multiplicando el volumen de la pirámide por 2, obtenemos el volumen del octaedro:
$latex V=2\times \frac{{{a}^3} \sqrt{2}}{6}$
$latex V=\frac{{{a}^3} \sqrt{2}}{3}$
Cómo calcular el área superficial de un octaedro
Para calcular el área superficial de un octaedro, usamos la siguiente fórmula:
| $latex A_{s}=2\sqrt{3}~{{a}^2}$ |
en donde, a es la longitud de uno de los lados del octaedro.
Demostración de la fórmula del área superficial de un octaedro
Podemos obtener la fórmula del área superficial de un octaedro al considerar que el área superficial de cualquier figura tridimensional es igual a la suma del área de todas sus caras.
En el caso de octaedros, tenemos ocho caras triangulares congruentes. Es decir, tenemos ocho caras con la misma forma y las mismas dimensiones, por lo que el área superficial es:
$latex A_{s}=8A_{t}$
en donde, $latex A_{t}$ es el área de cada cara triangular.
Además, cuando hablamos de un octaedro, normalmente nos referimos a un octaedro regular. Si este es el caso, cada cara triangular es un triángulo equilátero.
Entonces, recordando que la fórmula del área de un triángulo equilátero es:
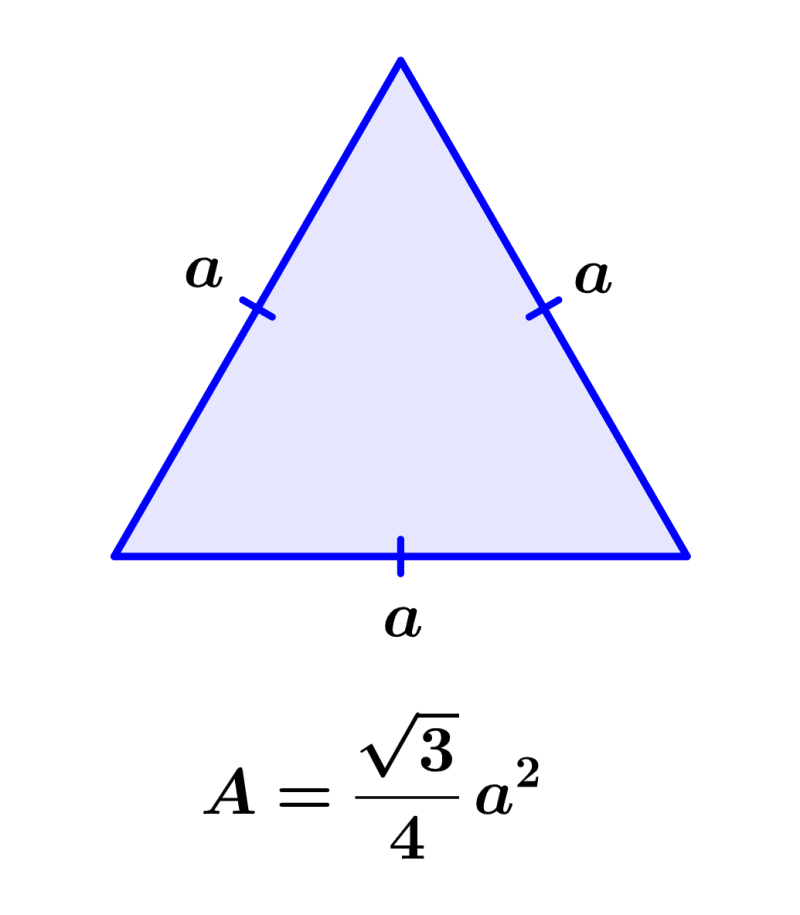
podemos sustituir ese valor en la fórmula del área superficial:
$latex A_{s}=8\times \frac{\sqrt{3}}{4}{{a}^2}$
$latex A_{s}=2\sqrt{3}~{{a}^2}$
Volumen y área de un octaedro – Ejercicios resueltos
EJERCICIO 1
Si es que un octaedro tiene lados con una longitud de 4 m, ¿cuál es su volumen?
Solución
Para resolver este ejercicio, tenemos que usar la fórmula del volumen de un octaedro con la longitud a=4. Entonces, tenemos:
$latex V=\frac{{{a}^3} \sqrt{2}}{3}$
$latex V=\frac{{{4}^3} \sqrt{2}}{3}$
$latex V=\frac{64 \sqrt{2}}{3}$
$latex V=30.17$
El volumen del octaedro es $latex 30.17 ~{{m}^3}$.
EJERCICIO 2
¿Cuál es el área superficial de un octaedro que tiene lados con una longitud de 2 m?
Solución
Podemos resolver este problema al usar la fórmula del área superficial de un octaedro con el valor a=2. Entonces, tenemos:
$latex A_{s}=2\sqrt{3}~{{a}^2}$
$latex A_{s}=2\sqrt{3}~{{2}^2}$
$latex A_{s}=2\sqrt{3}~4$
$latex A_{s}=13.86$
El área superficial del octaedro dado es $latex 13.86~{{m}^2}$
EJERCICIO 3
Calcula el volumen de un octaedro que tiene lados con una longitud de 5 m.
Solución
Nuevamente, usamos la fórmula del volumen de un tetraedro. En este caso, usamos el valor a=5:
$latex V=\frac{{{a}^3} \sqrt{2}}{3}$
$latex V=\frac{{{5}^3} \sqrt{2}}{3}$
$latex V=\frac{125 \sqrt{2}}{3}$
$latex V=58.93$
El volumen del octaedro es $latex 58.93 ~{{m}^3}$.
EJERCICIO 4
Encuentra el área superficial de un octaedro que tiene lados con una longitud de 5 cm.
Solución
Usamos la fórmula del área superficial, sustituyendo el valor a=5. Entonces, tenemos:
$latex A_{s}=2\sqrt{3}~{{a}^2}$
$latex A_{s}=2\sqrt{3}~{{5}^2}$
$latex A_{s}=2\sqrt{3}~25$
$latex A_{s}=86.6$
Entonces, el área superficial es $latex 86.6~{{cm}^2}$
EJERCICIO 5
Si es que un octaedro tiene lados con una longitud de 10 cm, ¿cuál es su volumen?
Solución
Vamos a usar la fórmula del volumen de un octaedro usando el valor a=10. Entonces, tenemos:
$latex V=\frac{{{a}^3} \sqrt{2}}{3}$
$latex V=\frac{{{10}^3} \sqrt{2}}{3}$
$latex V=\frac{1000 \sqrt{2}}{3}$
$latex V=471.4$
Entonces, el volumen del tetraedro dado es $latex 471.4 ~{{cm}^3}$.
EJERCICIO 6
Si es que un octaedro tiene lados con una longitud de 8 cm, ¿cuál es su área superficial?
Solución
Aplicamos la fórmula del área superficial con el valor a=8:
$latex A_{s}=2\sqrt{3}~{{a}^2}$
$latex A_{s}=2\sqrt{3}~{{8}^2}$
$latex A_{s}=2\sqrt{3}~64$
$latex A_{s}=221.7$
El área superficial del octaedro es $latex 221.7~{{cm}^2}$
EJERCICIO 7
Si es que el volumen de un octaedro es igual a $latex 11.5~{{m}^3}$, ¿cuál es la longitud de uno de sus lados?
Solución
En este caso, conocemos el volumen del octaedro y queremos calcular la longitud de los lados. Entonces, usamos la fórmula del volumen y resolvemos para a:
$latex V=\frac{{{a}^3} \sqrt{2}}{3}$
$latex 11.5=\frac{{{a}^3} \sqrt{2}}{3}$
$latex 34.5={{a}^3} \sqrt{2}$
$latex 24.4={{a}^3}$
$latex a=2.9$
La longitud de uno de los lados del octaedro es 2.9 m.
EJERCICIO 8
Si es que el área superficial de un octaedro es $latex 50~{{m}^2}$, ¿cuál es la longitud de sus lados?
Solución
En este caso, tenemos el área superficial del octaedro y queremos calcular la longitud de uno de sus lados. Entonces, tenemos que usar la fórmula del área superficial y resolver para a:
$latex A_{s}=2\sqrt{3}~{{a}^2}$
$latex 50=2\sqrt{3}~{{a}^2}$
$latex 14.43={{a}^2}$
$latex a=3.8$
Los lados del octaedro tienen una longitud de 3.8 m.
EJERCICIO 9
Calcula la longitud de los lados de un octaedro que tiene un volumen de $latex 22~{{cm}^3}$
Solución
Para resolver este ejercicio, tenemos que usar la fórmula del volumen de un octaedro y resolver para a. Entonces, tenemos:
$latex V=\frac{{{a}^3} \sqrt{2}}{3}$
$latex 22=\frac{{{a}^3} \sqrt{2}}{3}$
$latex 66={{a}^3} \sqrt{2}$
$latex 46.67={{a}^3}$
$latex a=3.6$
El octaedro tiene lados con una longitud de 3.6 cm.
EJERCICIO 10
Un octaedro tiene un área superficial de $latex 73.3~{{m}^2}$. Determina la longitud de uno de sus lados.
Solución
Vamos a usar la fórmula del área superficial con el área superficial dada y resolveremos para a:
$latex A_{s}=2\sqrt{3}~{{a}^2}$
$latex 73.3=2\sqrt{3}~{{a}^2}$
$latex 21.16={{a}^2}$
$latex a=4.6$
El octaedro tiene lados con una longitud de 4.6 m.
Volumen y área de un octaedro – Ejercicios para resolver
Si es el área superficial de un octaedro es 256.2 cm2, ¿cuál es la longitud de sus lados?
Escribe la respuesta a un lugar decimal.
Véase también
¿Interesado en aprender más sobre octaedros? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
