Existen varias transformaciones de funciones trigonométricas con las que podemos cambiar a las gráficas de las funciones trigonométricas estándar. Podemos realizar cambios en la amplitud, en el periodo, en la fase de la función. También podemos realizar traslaciones verticales y producir reflexiones de las gráficas.
A continuación, miraremos estas transformaciones de funciones trigonométricas a detalle junto con algunos ejemplos para visualizar el efecto de las transformaciones.
ÁLGEBRA
Relevante para…
Aprender a realizar transformaciones de funciones trigonométricas.
ÁLGEBRA
Relevante para…
Aprender a realizar transformaciones de funciones trigonométricas.
Amplitud de funciones trigonométricas
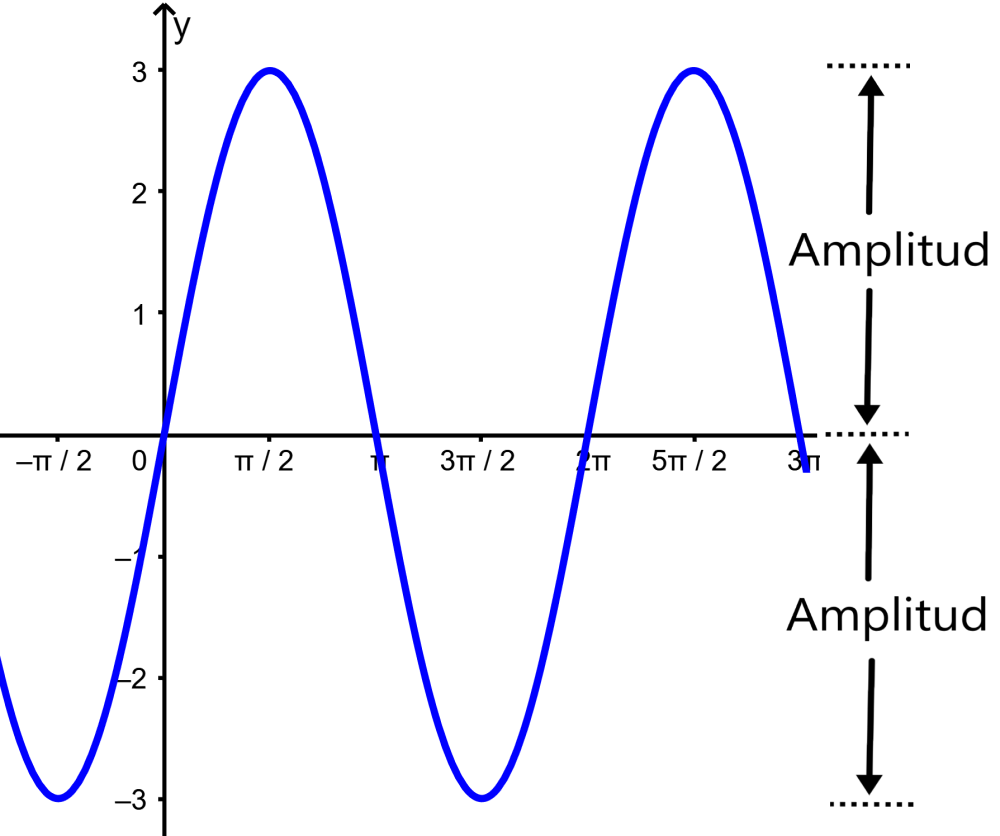
La amplitud de una función trigonométrica es el máximo desplazamiento en la gráfica de esa función. La amplitud es la distancia desde el valor promedio de la curva a su valor máximo o mínimo.
En el caso de las funciones seno y coseno, la amplitud es el valor del coeficiente líder de la función. Podemos cambiar la amplitud de estas funciones, al multiplicar a la función por una constante A. Por ejemplo, si es que la función es $latex y=A\sin(x)$, entonces la amplitud es |A|.
En el caso de las funciones tangente, cosecante, secante y cotangente, la amplitud será infinitamente grande sin importar el valor de A.
Periodo de funciones trigonométricas
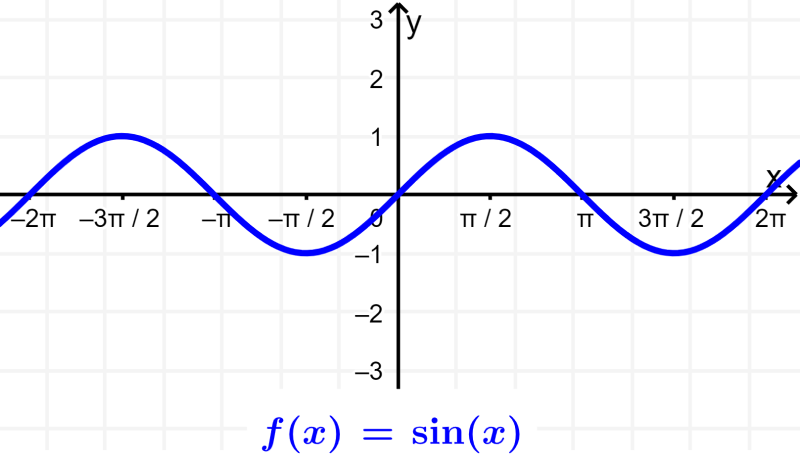
El periodo de una función trigonométrica es la longitud de un ciclo. Es decir, el periodo es el desplazamiento de x en el que la gráfica de la función se empieza a repetir. Por ejemplo, consideremos a la función $latex y=\sin(x)$:
El valor $latex x=2\pi$ es el punto en el que la gráfica se empieza a repetir.
El coeficiente de x es la constante que determina el periodo. La forma general es $latex y=\sin(Bx)$, en donde B determina el periodo. Para las funciones seno, coseno, secante y cosecante, el periodo es $latex 2\pi$ y podemos cambiar el periodo de acuerdo con la fórmula:
$latex \text{periodo}=\frac{\text{periodo original}}{|B|}$
Cuando |B| es mayor que 1, el nuevo periodo es más pequeño que el original, por lo que la función pareciera tener una compresión horizontal. Cuando |B| es menor que 1, la función pareciera tener un estiramiento horizontal.
Las funciones tangente y cotangente tienen un periodo de $latex \pi$.
Fase de funciones trigonométricas
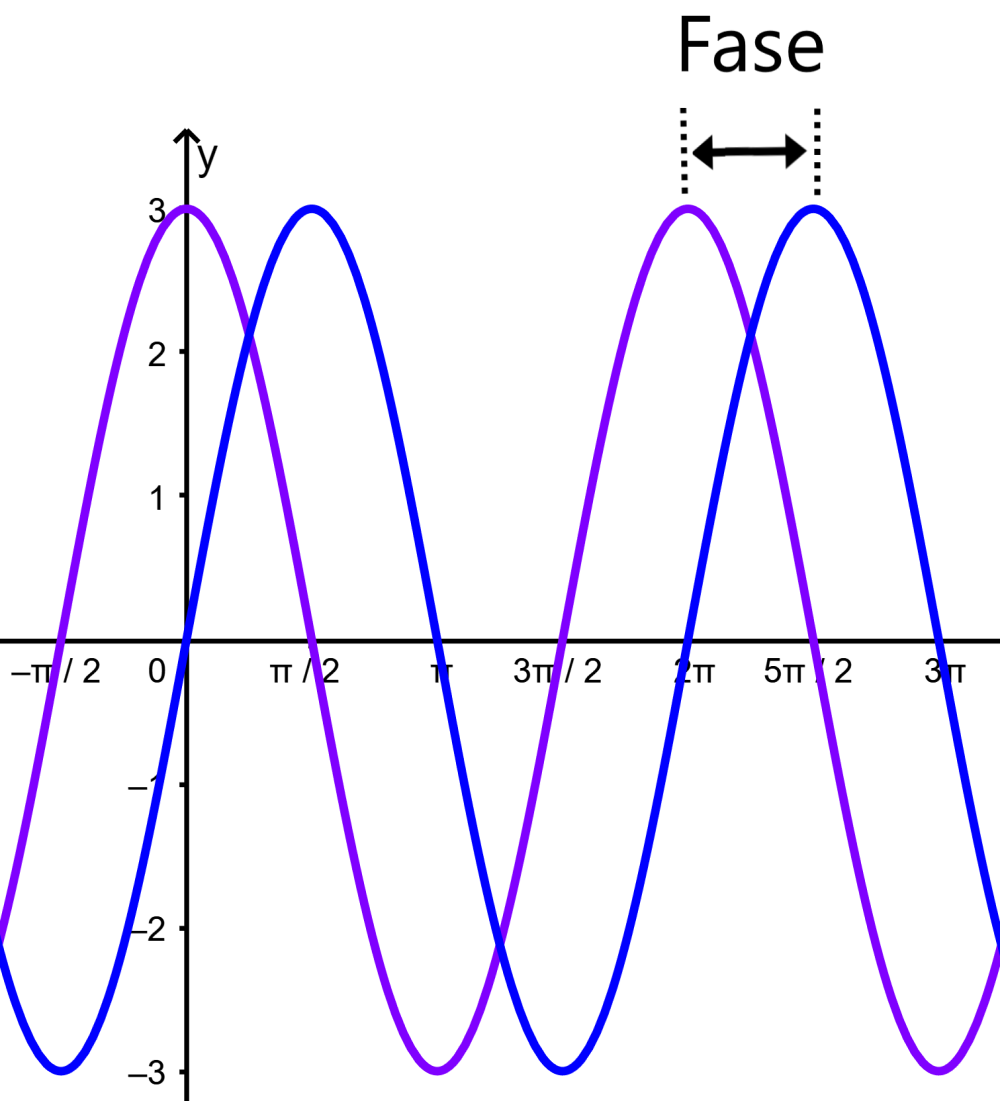
La fase de una función trigonométrica se refiere a la translación horizontal hacia la derecha de la gráfica de la función.
La forma general de la función trigonométrica es $latex y=A \sin B(x-C)$, en donde A es la amplitud, B es el periodo y C es la fase.
La gráfica de $latex y=\sin(x)$ puede ser trasladada hacia la derecha o la izquierda. Si es que C es positivo, la traslación es hacia la derecha y si es que C es negativo, la traslación es hacia la izquierda.
Traslación vertical
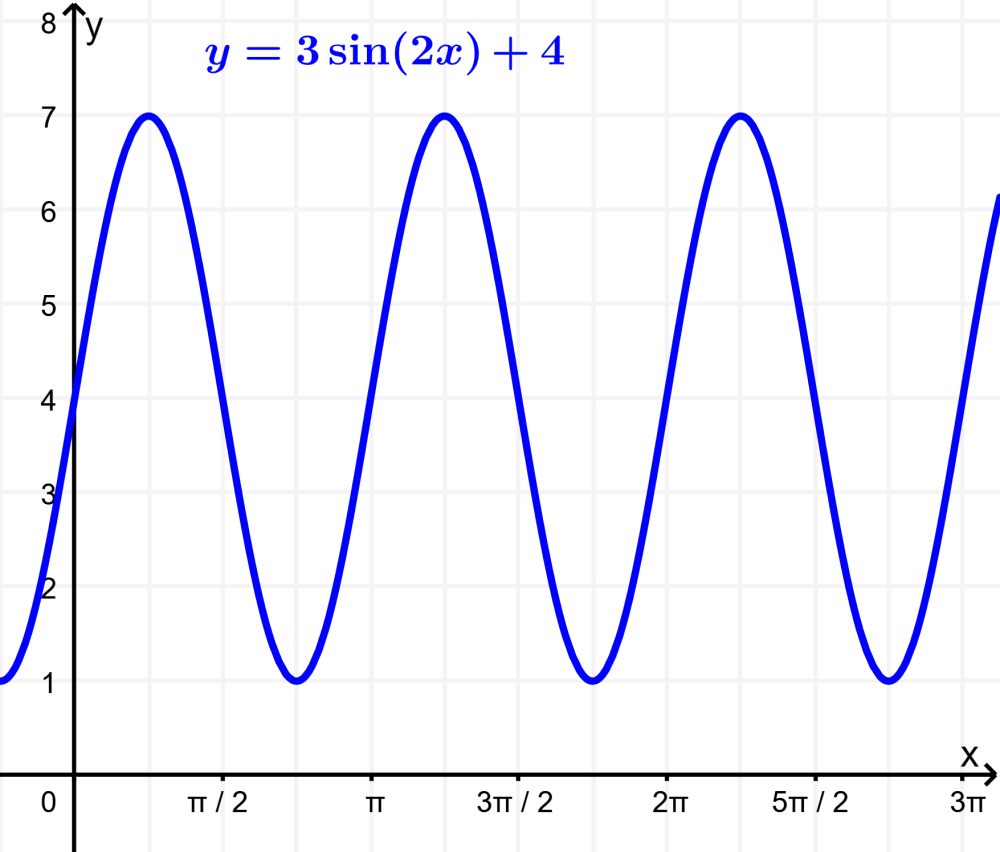
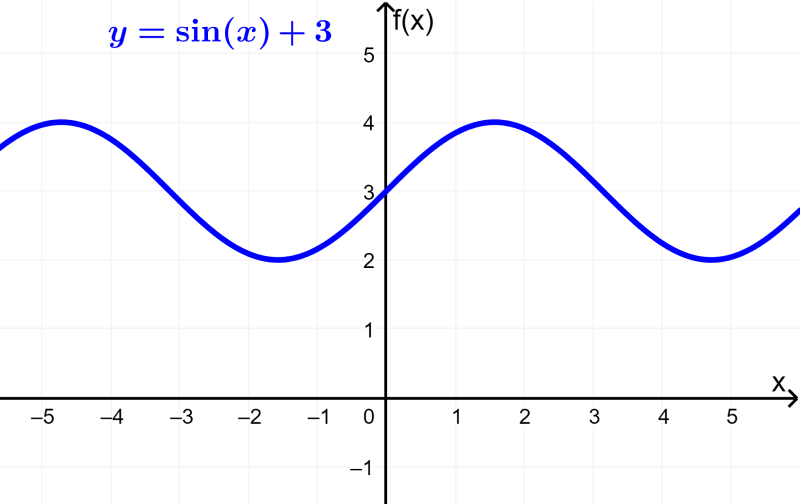
Al añadir un valor D a la función trigonométrica, traslaremos a su gráfica verticalmente. Si es que D es positivo, la gráfica se moverá hacia arriba por un factor de D y si es que D es negativo, la gráfica se moverá hacia abajo.
La forma general de la función seno con una traslación vertical es $latex y=A\sin B(x-C)+D$.
Reflexiones
Para obtener la gráfica de:
- $latex y=-f(x)$ reflejamos a la gráfica de $latex y=f(x)$ con respecto al eje x
- $latex y=f(-x)$ reflejamos a la gráfica de $latex y=f(x)$ con respecto al eje y
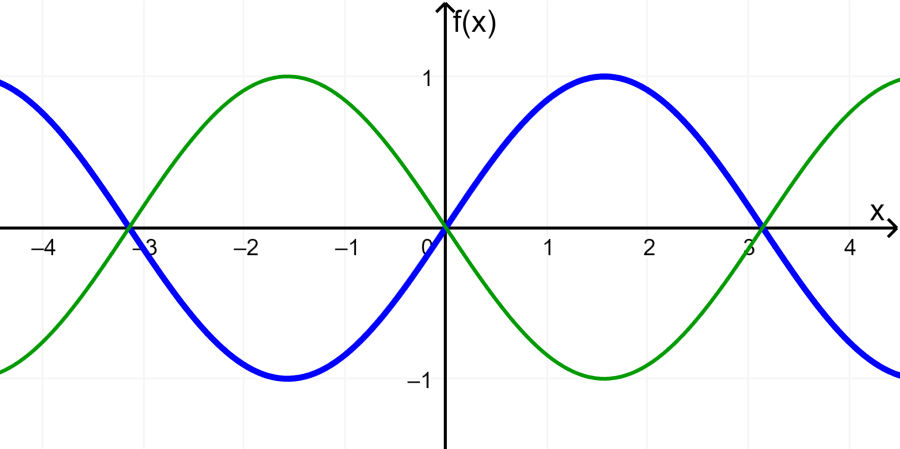
La siguiente gráfica muestra a la función seno en azul, es decir, la función $latex y=\sin(x)$. La función en verde representa tanto a la función $latex y=-f(x)$ como a la función $latex y=f(-x)$. En este caso particular, la reflexión en x de la función es igual a la reflexión en y.
Ejemplos de funciones trigonométricas con transformaciones
EJEMPLO 1
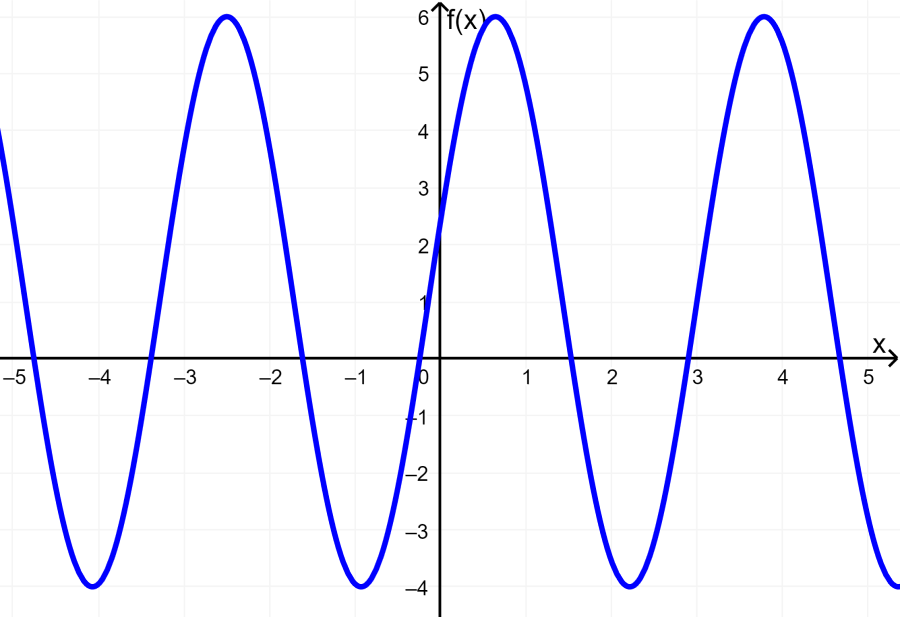
- La siguiente es la gráfica de la función $latex y=5\sin(2(x-3))+1$.
Aquí, tenemos:
- Amplitud: $latex A=5$
- Periodo: $latex \text{periodo}=\frac{2\pi}{B}=\frac{2\pi}{2}=\pi$
- Fase: $latex C=3$
- Traslación vertical: $latex D=1$
EJEMPLO 2
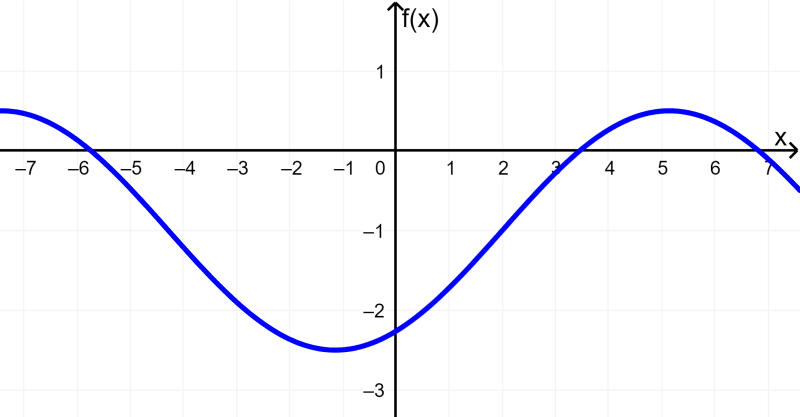
- La siguiente es la gráfica de la función $latex y=1.5\sin(0.5(x-2))-1$.
Esta función tiene lo siguiente:
- Amplitud: $latex A=1.5$
- Periodo: $latex \text{periodo}=\frac{2\pi}{B}=\frac{2\pi}{0.5}=4\pi$
- Fase: $latex C=2$
- Traslación vertical: $latex D=-1$
EJEMPLO 3
- La siguiente es la gráfica de la función $latex y=3\sin(2(x+3))-2$.
En esta función, tenemos:
- Amplitud: $latex A=2$
- Periodo: $latex \text{periodo}=\frac{2\pi}{B}=\frac{2\pi}{2}=\pi$
- Fase: $latex C=-3$
- Traslación vertical: $latex D=-2$
Véase también
¿Interesado en aprender más sobre funciones algebraicas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
