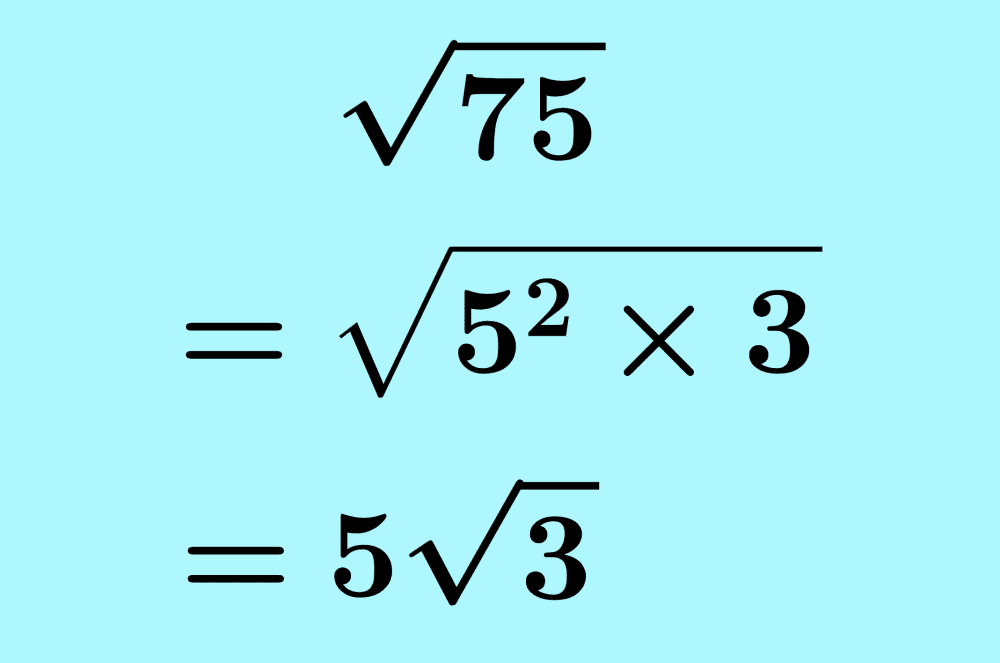Las expresiones radicales son expresiones que contienen raíces cuadradas, raíces cúbicas u otras raíces. Podemos simplificar radicales al descomponer al número en sus factores y aplicar los radicales a factores repetidos.
En este artículo, conoceremos cómo simplificar radicales paso a paso. Luego, veremos varios ejemplos y problemas de práctica para aplicar lo aprendido.
¿Cómo simplificar radicales?
Los radicales pueden ser simplificados al encontrar factores que pueden ser sacados del radical. Para esto, seguimos estos pasos:
Paso 1: Identifica el radicando. El radicando es el número o expresión dentro del radical. En la expresión $latex \sqrt{a}$, ‘a‘ es el radicando.
Paso 2: Factoriza el radicando al dividirlo en sus factores primos.
Nota: Los factores primos son los números primos forman el número original al ser multiplicados. Por ejemplo, los factores primos de 12 son 2, 2 y 3 (ya que 2 × 2 × 3 = 12).
Paso 3: Determina el índice del radical. El índice del radical es la raíz que estamos tomando. Para una raíz cuadrada, el índice es 2; para una raíz cúbica, el índice es 3; y así sucesivamente.
Paso 4: Simplifica el radical. Para simplificar el radical, tenemos que encontrar los factores que se pueden sacar del radical. Para una raíz cuadrada, necesitamos pares del mismo factor; para una raíz cúbica, necesitamos triples del mismo factor, etc.
Por ejemplo, si estamos simplificando la raíz cuadrada de 12, que tiene los factores primos 2, 2 y 3, podemos sacar un par de 2s como un 2, y nos queda $latex \sqrt{3}$. Entonces, $latex \sqrt{12}$ se simplifica a $latex 2\sqrt{3}$.
Paso 5: Combinar términos semejantes si los hay. Si la expresión radical tiene múltiples términos, podemos combinar términos semejantes para simplificar aún más la expresión.
Nota: En el caso de expresiones radicales, los términos semejantes son términos con el mismo radicando. Por ejemplo, si tenemos $latex 3\sqrt{2}+4\sqrt{2}$, podemos combinar los coeficientes (3 y 4) para obtener $latex 7\sqrt{2}$.
10 Ejercicios resueltos de simplificación de radicales
EJERCICIO 1
Simplifica la expresión: $latex \sqrt{72}$
Solución
Paso 1: El radicando es 72.
Paso 2: Los factores primos de 72 son 2, 2, 2, 3 y 3 (ya que 2 × 2 × 2 × 3 × 3 = 72).
$latex \sqrt{72}=\sqrt{2 \times 2 \times 2 \times 3 \times 3}$
Paso 3: El índice es 2 porque es una raíz cuadrada.
Paso 4: Tenemos un par de 2s y un par de 3s. Podemos sacar ambos del radical:
$latex 2 \times 3 \times \sqrt{2} = 6\sqrt{2}$
Paso 5: No hay términos semejantes en esta expresión, por lo que la expresión simplificada es $latex 6\sqrt{2}$.
EJERCICIO 2
Encuentra la versión más simplificada de $latex \sqrt[3]{54}$
Solución
Paso 1: El radicando es 54.
Paso 2: Los factores primos de 54 son 2, 3, 3 y 3 (ya que 2 × 3 × 3 × 3 = 54).
$latex \sqrt[3]{54}=\sqrt{2 \times 3 \times 3 \times 3 }$
Paso 3: El índice es 3 porque es una raíz cúbica.
Paso 4: Tenemos un triplete de 3s, así que podemos sacarlo del radical:
$latex 3 \times \sqrt[3]{2} = 3\sqrt[3]{2}$.
Paso 5: No hay términos semejantes en esta expresión, por lo que la expresión simplificada es $latex 3\sqrt[3]{2}$.
EJERCICIO 3
Usa factores primos para simplificar $latex \sqrt{200}$
Solución
Paso 1: El radicando es 200.
Paso 2: Los factores primos de 200 son 2, 2, 2, 5 y 5 ( 2 × 2 × 2 × 5 × 5 = 200).
$latex \sqrt{200}=\sqrt{2 \times 2 \times 2 \times 5 \times 5}$
Paso 3: El índice es 2, ya que es una raíz cuadrada.
Paso 4: Tenemos un par de 2s y un par de 5s. Podemos sacar ambos del radical:
$latex 2 \times 5 \times \sqrt{2} = 10\sqrt{2}$
Paso 5: No hay términos semejantes en esta expresión, por lo que la expresión simplificada es $latex 10\sqrt{2}$.
EJERCICIO 4
Simplifica la expresión $latex \sqrt{98}$
Solución
Paso 1: El radicando es 98.
Paso 2: Los factores primos de 98 son 2, 7 y 7 (ya que 2 × 7 × 7 = 98).
$latex \sqrt{98}=\sqrt{2 \times 7 \times 7 }$
Paso 3: El índice es 2 porque es una raíz cuadrada.
Paso 4: Tenemos un par de 7s, así que podemos sacarlo del radical:
$latex 7 \times \sqrt{2} = 7\sqrt{2}$
Paso 5: No hay términos semejantes en esta expresión, por lo que la expresión simplificada es $latex 7\sqrt{2}$.
EJERCICIO 5
Si tenemos la expresión $latex \sqrt[4]{162}$, ¿cuál es su forma simplificada?
Solución
Paso 1: El radicando es 162.
Paso 2: Los factores primos de 162 son 2, 3, 3, 3 y 3 (ya que 2 × 3 × 3 × 3 × 3 = 162).
$latex \sqrt[4]{162}=\sqrt{2 \times 3 \times 3 \times 3 \times 3}$
Paso 3: El índice es 4 porque es una raíz cuarta.
Paso 4: Tenemos dos pares de 3s, así que podemos sacar un 3 del radical:
$latex 3 \times \sqrt[4]{2 } = 3\sqrt[4]{2}$
Paso 5: No hay términos semejantes en esta expresión, por lo que la expresión simplificada es $latex 3\sqrt[4]{2}$.
EJERCICIO 6
Simplifica la expresión $latex \sqrt[3]{500}$
Solución
Paso 1: El radicando es 500.
Paso 2: Los factores primos de 500 son 2, 2, 5, 5 y 5 (ya que 2 × 2 × 5 × 5 × 5 = 500).
$latex \sqrt{500}=\sqrt{2 \times 2 \times 5 \times 5 \times 5}$
Paso 3: El índice es 3.
Paso 4: Tenemos un triplete de 5s, así que podemos sacarlo del radical:
$latex 5 \times \sqrt[3]{2 \times 2} = 5\sqrt[3]{4}$
Paso 5: En esta expresión no hay términos semejantes, por lo que la expresión simplificada es $latex 5\sqrt[3]{4}$.
EJERCICIO 7
Encuentra la forma simplificada de $latex \sqrt{18}+\sqrt{72}$
Solución
Paso 1: Los radicandos son 18 y 72.
Paso 2: Factorizar los radicandos:
- Los factores primos de 18 son 2, 3 y 3 (ya que 2 × 3 × 3 = 18).
- Los factores primos de 72 son 2, 2, 2, 3 y 3 (ya que 2 × 2 × 2 × 3 × 3 = 72).
Paso 3: El índice es 2 en ambos radicales.
Paso 4: Simplifica los radicales:
- $latex \sqrt{18}$: Tenemos un par de 3s, así que podemos sacarlo del radical para obtener $latex 3\sqrt{2}$.
- $latex \sqrt{72}$: Tenemos un par de 2s y un par de 3s, por lo que tenemos $latex 6\sqrt{2}$.
Paso 5: Ambos términos tienen el mismo radicando ($latex \sqrt{2}$), por lo que podemos sumar los coeficientes:
$latex 3\sqrt{2} + 6\sqrt{2} = 9\sqrt{2}$
EJERCICIO 8
Simplifica la expresión $latex 3\sqrt{50}+5\sqrt{200}$
Solución
Paso 1: Los radicandos son 50 y 200.
Paso 2: Factorizar los radicandos:
- Los factores primos de 50 son 2, 5 y 5 (ya que 2 × 5 × 5 = 50).
- Los factores primos de 200 son 2, 2, 2, 5 y 5 (ya que 2 × 2 × 2 × 5 × 5 = 200).
Paso 3: El índice es 2 en ambos.
Paso 4: Simplifica los radicales:
- En $latex 3\sqrt{50}$, simplificamos a $latex \sqrt{50}$: Tenemos un par de 5s, así que podemos sacarlo del radical: $latex 3 \times 5\sqrt{2} = 15\sqrt{2}$.
- En $latex 5\sqrt{200}$, simplificamos a $latex \sqrt{200}$: Tenemos un par de 2s y un par de 5s: $latex 5 \times 10\sqrt{2}$ = 50\sqrt{2}$
Paso 5: Ambos términos tienen el mismo radicando ($latex \sqrt{2}$), por lo que podemos sumar los coeficientes:
$latex 15\sqrt{2} + 50\sqrt{2} = 65\sqrt{2}$
EJERCICIO 9
Si tenemos la expresión $latex \sqrt{45}+2\sqrt{20}$, ¿cuál es su forma simplificada?
Solución
Paso 1: Los radicandos son 45 y 20.
Paso 2: Factorizar los radicandos:
- Los factores primos de 45 son 3, 3 y 5 (ya que 3 × 3 × 5 = 45).
- Los factores primos de 20 son 2, 2, 5 (ya que 2 × 2 × 5 = 20).
Paso 3: El índice es 2 en ambos.
Paso 4: Simplifica los radicales:
- $latex \sqrt{45}$: Tenemos un par de 3s, así que podemos sacarlo del radical: $latex 3\sqrt{5}$.
- $latex 2\sqrt{20}$: Tenemos un par de 2s, así que podemos sacarlo del radical: $latex 2 \times 2\sqrt{5} = 4\sqrt{5}$.
Paso 5: Ambos términos tienen el mismo radicando ($latex \sqrt{5}$), por lo que podemos sumar los coeficientes:
$latex 3\sqrt{5} + 4\sqrt{5} = 7\sqrt{5}$
EJERCICIO 10
Encuentra la forma simplificada de $latex 4\sqrt{32}+3\sqrt{8}$
Solución
Paso 1: Los radicandos son 32 y 8.
Paso 2: Factorizar los radicandos:
- Los factores primos de 32 son 2, 2, 2, 2 y 2 (ya que $latex 2^5 = 32$).
- Los factores primos de 8 son 2, 2 y 2 (ya que $latex 2^3 = 8$).
Paso 3: El índice es 2 en ambos.
Paso 4: Simplifica los radicales:
- $latex 4\sqrt{32}$: Tenemos dos pares de 2s, así que podemos sacar ambos del radical: $latex 4 \times 4\sqrt{2} = 16\sqrt{2}$.
- $latex 3\sqrt{8}$: Tenemos un par de 2s, así que podemos sacarlo del radical: $latex 3 \times 2\sqrt{2} = 6\sqrt{2}$.
Paso 5: Sumamos los coeficientes de los radicandos:
$latex 16\sqrt{2} + 6\sqrt{2} = 22\sqrt{2}$
Ejercicios de simplificación de radicales para resolver
Simplifica la expresión $latex \sqrt{16} + \sqrt{81}$.
Escribe la respuesta en la casilla.
Véase también
¿Interesado en aprender más sobre radicales? Puedes mirar estas páginas:
–
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
