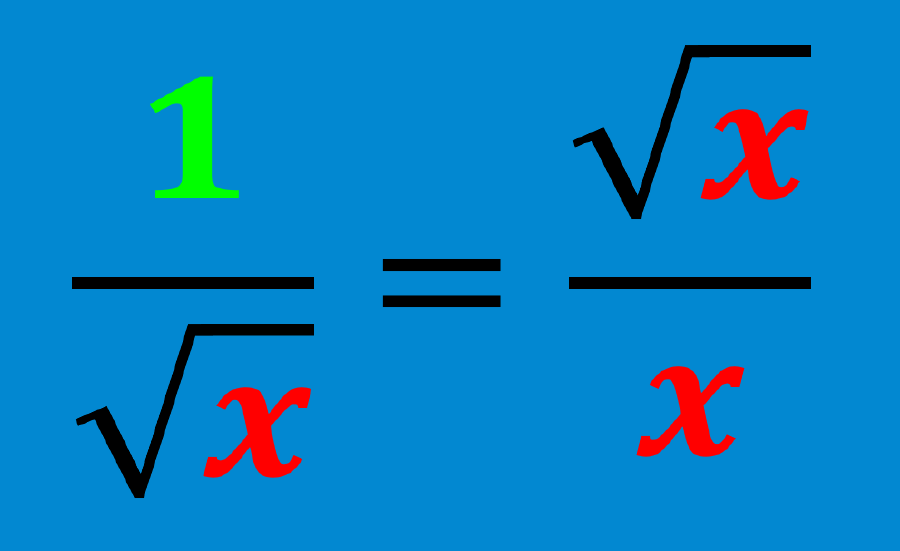Las expresiones que tienen radicales, es decir, raíces cuadradas, raíces cúbicas u otras en el denominador, pueden ser racionalizadas para eliminar esos radicales del denominador. Existen dos tipos principales de racionalización que podemos aplicar dependiendo en si el denominador es un monomio o un binomio.
Miraremos estos dos tipos de racionalizaciones junto con ejemplos para facilitar el entendimiento.
¿Qué es la racionalización de denominadores?
La racionalización de denominadores significa eliminar cualquier radical en el denominador como raíces cuadradas, raíces cúbicas u otras. La idea principal es multiplicar la fracción original por un valor apropiado, de tal forma que después de simplificar, el denominador ya no tenga ningún radical.
La idea de racionalizar un denominador tal vez tiene más sentido si es que consideramos la definición de racionalizar. Recordemos que los números 4, $latex \frac{1}{3}$ y 0.75 son conocidos como números racionales, es decir, estos números pueden ser expresados como una razón de dos números enteros $latex \frac{4}{1}$, $latex \frac{1}{3}$ y $latex \frac{3}{4}$ respectivamente.
Algunos radicales son irracionales, ya que no pueden ser representados como la razón de dos números enteros. Por lo tanto, el punto de racionalizar el denominador es para cambiar la expresión de modo que el denominador se vuelva un número racional.
Racionalización de denominadores con un término
Empecemos con la fracción $latex \frac{1}{{\sqrt{3}}}$. Su denominador es $latex {\sqrt{3}}$, el cual es un número irracional. Esto hace que sea difícil encontrar el valor exacto de $latex \frac{1}{{\sqrt{3}}}$.
Sabemos que es posible multiplicar a esta fracción por 1 sin cambiar su valor. También sabemos que $latex \frac{{\sqrt{3}}}{{\sqrt{3}}}$ es igual a 1, por lo que podemos multiplicar por esa expresión:
$latex \frac{1}{{\sqrt{3}}}\times \frac{{\sqrt{3}}}{{\sqrt{3}}}$
$latex =\frac{{\sqrt{3}}}{{\sqrt{{3\times 3}}}}$
$latex =\frac{{\sqrt{3}}}{{\sqrt{9}}}$
$latex =\frac{{\sqrt{3}}}{3}$
El denominador de la fracción ya no es un radical.
Decidimos multiplicar por $latex \frac{{\sqrt{3}}}{{\sqrt{3}}}$ debido a que sabemos que la raíz cuadrada de un número multiplicada por sí mismo será igual a un número entero. Tenemos la expresión $latex \sqrt{x}\times \sqrt{x}=x$.
Entonces, para racionalizar expresiones que tienen solo un término que es un radical en el denominador, multiplicamos tanto al denominador como al numerador por ese radical y simplificamos. Podemos mirar esto en los siguientes ejemplos.
EJEMPLO 1
Racionaliza el denominador de la expresión $latex \frac{4}{{\sqrt{2}}}$.
Solución: Vemos que el denominador contiene una expresión radical, la raíz cuadrada de 2. Eliminamos al radical al multiplicar al denominador por sí mismo, pero para no afectar a la expresión, también multiplicamos al numerador. Entonces, multiplicamos por la expresión $latex \frac{{\sqrt{2}}}{{\sqrt{2}}}$:
$latex \frac{4}{{\sqrt{2}}}\times \frac{{\sqrt{2}}}{{\sqrt{2}}}$
$latex =\frac{{4\sqrt{2}}}{{\sqrt{4}}}$
Ahora podemos simplificar el radical en el denominador y simplificar la fracción resultante de ser posible:
$latex =\frac{{4\sqrt{2}}}{2}$
$latex =2\sqrt{2}$
EJEMPLO 2
Racionaliza el denominador de la expresión $latex \frac{5}{{\sqrt{3}}}$.
Solución: En este caso, tenemos a la raíz cuadrada de 3 en el denominador. Para racionalizar, multiplicamos al denominador y el numerador por la raíz cuadrada de 3. Entonces, multiplicamos por la expresión $latex \frac{{\sqrt{3}}}{{\sqrt{3}}}$:
$latex \frac{5}{{\sqrt{3}}}\times \frac{{\sqrt{3}}}{{\sqrt{3}}}$
$latex =\frac{{5\sqrt{3}}}{{\sqrt{9}}}$
Ahora podemos simplificar el radical en el denominador:
$latex =\frac{{5\sqrt{3}}}{3}$
En este caso, ya no podemos simplificar más.
EJEMPLO 3
Simplifica al racionalizar el denominador de la expresión $latex \frac{{5\sqrt{{10}}}}{{\sqrt{2}}}$.
Solución: Similar a los problemas anteriores, multiplicamos por la expresión $latex \frac{{\sqrt{2}}}{{\sqrt{2}}}$:
$latex \frac{{5\sqrt{{10}}}}{{\sqrt{2}}}\times \frac{{\sqrt{2}}}{{\sqrt{2}}}$
$latex =\frac{{5\sqrt{{20}}}}{{\sqrt{4}}}$
Ahora podemos simplificar el radical en el denominador. Pero también observamos que podemos reescribir al radical en el numerador para simplificar un poco:
$latex =\frac{{5\sqrt{{4\times 5}}}}{2}$
$latex =\frac{{5\times 2\sqrt{5}}}{2}$
$latex =5\sqrt{5}$
Inténtalo tú mismo – Resuelve los ejercicios
¿Cuántos casos hay de racionalización de denominadores?
Podemos distinguir dos casos más importantes de racionalización de denominadores basándonos en el número de términos que la expresión tiene en el denominador. La racionalización de denominadores con un término que vimos anteriormente es un caso de racionalización de denominadores.
| Irracional | Racional | |
| $latex \frac{1}{{\sqrt{3}}}$ | = | $latex \frac{{\sqrt{3}}}{3}$ |
| $latex \frac{{3+\sqrt{2}}}{{\sqrt{2}}}$ | = | $latex \frac{{3\sqrt{2}+2}}{2}$ |
Adicionalmente, también tenemos la racionalización de denominadores con dos términos o también conocida como racionalización de denominadores con binomios.
| Irracional | Racional | |
| $latex \frac{4}{{\sqrt{6}+5}}$ | = | $latex \frac{{4\sqrt{6}-20}}{{-19}}$ |
| $latex \frac{2}{{3+\sqrt{3}}}$ | = | $latex \frac{{3-\sqrt{3}}}{3}$ |
→ Calculadora de Racionalización
¿Cómo racionalizar el denominador de un binomio?
Los denominadores no siempre contienen un solo término, muchas veces tenemos denominadores de un binomio. Los siguientes son los pasos requeridos para racionalizar el denominador de un binomio:
Paso 1: Para racionalizar el denominador, tenemos que multiplicar tanto al numerador como al denominador por el conjugado del denominador. Recuerda que para encontrar el conjugado, lo único que tenemos que hacer es cambiar el signo que va entre los términos.
Paso 2: Realizar la multiplicación al distribuir tanto al numerador como al denominador.
Paso 3: Combinar términos semejantes.
Paso 4: Simplificar los radicales.
Paso 5: Combinar términos semejantes.
Paso 6: Reducir la fracción si es que es posible.
EJEMPLO 1
Racionaliza el denominador de la expresión $latex \frac{3}{{\sqrt{3}+4}}$.
Paso 1: Multiplicamos al numerador y al denominador por el conjugado del denominador:
$latex \frac{3}{{\sqrt{3}+4}}\times \frac{{\sqrt{3}-4}}{{\sqrt{3}-4}}$
Paso 2: Distribuimos la multiplicación:
$latex \frac{{3\sqrt{3}-12}}{{\sqrt{9}+4\sqrt{3}-4\sqrt{3}-16}}$
Paso 3: Combinamos términos semejantes:
$latex \frac{{3\sqrt{3}-12}}{{\sqrt{9}-16}}$
Paso 4: Simplificamos los radicales:
$latex \frac{{3\sqrt{3}-12}}{{3-16}}$
Paso 5: Combinamos términos semejantes:
$latex \frac{{3\sqrt{3}-12}}{{-13}}$
Paso 6: La fracción ya no puede ser reducida.
EJEMPLO 2
Racionaliza el denominador de la expresión $latex \frac{{3\sqrt{6}+2\sqrt{3}}}{{4\sqrt{6}+3\sqrt{3}}}$.
Paso 1: Empezamos multiplicando al numerador y al denominador por el conjugado del denominador:
$$\frac{{3\sqrt{6}+2\sqrt{3}}}{{4\sqrt{6}+3\sqrt{3}}}\times \frac{{4\sqrt{6}-3\sqrt{3}}}{{4\sqrt{6}-3\sqrt{3}}}$$
Paso 2: Aplicamos y distribuimos la multiplicación:
$$\frac{{12\sqrt{{36}}+8\sqrt{{18}}-9\sqrt{{18}}-6\sqrt{9}}}{{16\sqrt{{36}}+12\sqrt{{18}}-12\sqrt{{18}}-9\sqrt{9}}}$$
Paso 3: Combinamos términos semejantes:
$latex \frac{{12\sqrt{{36}}-\sqrt{{18}}-6\sqrt{9}}}{{16\sqrt{{36}}-9\sqrt{9}}}$
Paso 4: Simplificamos los radicales:
$latex \frac{{12\left( 6 \right)-3\sqrt{2}-6\left( 3 \right)}}{{16\left( 6 \right)-9\left( 3 \right)}}$
$latex =\frac{{72-3\sqrt{2}-18}}{{96-27}}$
Paso 5: Combinamos términos semejantes:
$latex \frac{{64-3\sqrt{2}}}{{69}}$
Paso 6: La fracción ya no puede ser reducida.
EJEMPLO 3
Racionaliza el denominador de la expresión $latex \frac{{2\sqrt{8}}}{{3\sqrt{6}-5\sqrt{2}}}$.
Paso 1: Empezamos multiplicando al numerador y al denominador por el conjugado del denominador:
$$\frac{{2\sqrt{8}}}{{3\sqrt{6}-5\sqrt{2}}}\times \frac{{3\sqrt{6}+5\sqrt{2}}}{{3\sqrt{6}+5\sqrt{2}}}$$
Paso 2: Aplicamos y distribuimos la multiplicación:
$$\frac{{12\sqrt{{36}}+8\sqrt{{18}}-9\sqrt{{18}}-6\sqrt{9}}}{{16\sqrt{{36}}+12\sqrt{{18}}-12\sqrt{{18}}-9\sqrt{9}}}$$
Paso 3: Combinamos términos semejantes:
$latex \frac{{6\sqrt{{48}}+10\sqrt{{16}}}}{{9\sqrt{{36}}-25\sqrt{4}}}$
Paso 4: Simplificamos los radicales:
$latex \frac{{6\left( {4\sqrt{3}} \right)+10\left( 4 \right)}}{{9\left( 6 \right)-25\left( 2 \right)}}$
$latex =\frac{{24\sqrt{3}+40}}{{54-50}}$
Paso 5: Combinamos términos semejantes:
$latex \frac{{24\sqrt{3}+40}}{4}$
Paso 6: Simplificamos la fracción.
$latex 6\sqrt{3}+10$
Inténtalo tú mismo – Resuelve los ejercicios
Véase también
¿Interesado en aprender más sobre expresiones algebraicas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
