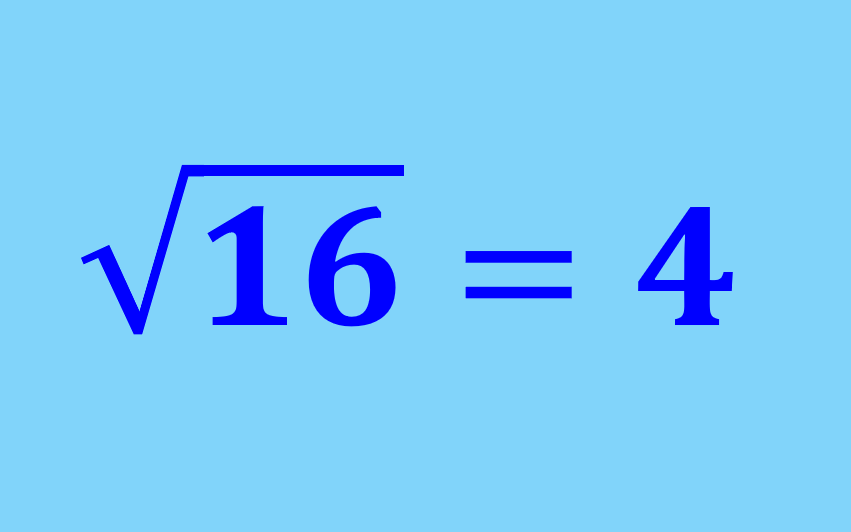La raíz cuadrada puede ser considerada la operación opuesta de elevar a un número al cuadrado. Con la raíz cuadrada, estamos buscando un número el cual al ser elevado al cuadrado produce el número debajo de la raíz cuadrada.
A continuación, mirararemos un resumen de la raíz cuadrada. Además, veremos ejercicios resueltos para entender cómo resolver este tipo de problemas.
Resumen de raíz cuadrada
Las raíces cuadradas son lo opuesto de elevar a un número al cuadrado o multiplicarlo por sí mismo. Por ejemplo, 4 elevado al cuadrado es igual a 16 $latex ({{4}^2}=16)$, por lo que la raíz cuadrada de 16 es igual a 4. Usando símbolos matemáticos, tenemos:
$latex \sqrt{16} = 4$dEl símbolo “√” nos indica que debemos sacar la raíz cuadrada de un número. Es importante recordar que en realidad todos los números tienen dos raíces cuadradas.
Por ejemplo, cuatro multiplicado por cuatro es igual a dieciseis, pero cuatro negativo multiplicado por cuatro negativo también es igual a dieciseis. Entonces, tenemos:
$latex \sqrt{16} = \pm4$
En algunos casos, podemos ignorar las raíces cuadradas negativas de los números, pero en algunas ocasiones es importante recordar que cada número tiene dos raíces cuadradas.dUno de los desafíos con las raíces cuadradas puede ser la simplificación de raíces cuadradas grandes.
Para realizar esto, tenemos que seguir unas simples reglas. Podemos factorizar las raíces cuadradas en la misma manera que factorizamos números. Por ejemplo, si tenemos la raíz cuadrada de seis, podemos escribir lo siguiente: d$latex \sqrt{6}=\sqrt{2}\sqrt{3}$
Ejercicios de raíz cuadrada resueltos
Estos ejercicios de raíz cuadrada pueden ser usados para dominar la resolución de problemas con raíces cuadradas. Cada ejercicio tiene su respectiva solución, pero es recomendable que intentes resolver los ejercicios tú mismo antes de mirar la respuesta.
En los siguientes ejercicios, solo tomamos en cuenta a la raíz cuadrada positiva del número.
EJERCICIO 1
Encuentra lo siguiente: $latex \sqrt{25}$.
Solución
Tenemos que encontrar un número el cual al ser multiplicado por sí mismo produzca el 25. La respuesta es 5, ya que si es que multiplicamos al 5 por sí mismo, obtenemos:
$latex 5\times 5=25$
EJERCICIO 2
Encuentra la raíz cuadrada de 121: $latex \sqrt{121}$.
Solución
Tenemos que encontrar un número el cual al ser multiplicado por sí mismo, resulte en 121. Este número es igual a 11, ya que al elevar el 11 al cuadrado, obtenemos:
$latex {{11}^2}=121$
EJERCICIO 3
Encuentra lo siguiente: $latex \sqrt{32}$.
Solución
En este caso, no existe un número entero que pueda ser multiplicado por sí mismo para obtener 32. Sin embargo, podemos factorizar esta expresión y escribir de la siguiente manera:
$latex \sqrt{32}=\sqrt{16}\sqrt{2}$
Ahora, podemos encontrar la raíz cuadrada de 16. Sabemos que al multiplicar al 4 por sí mismo obtenemos 16, entonces, tenemos:
$latex \sqrt{16}\sqrt{2}=4\sqrt{2}$
EJERCICIO 4
Simplifica lo siguiente: $latex \sqrt{50}$.
Solución
En este caso, tampoco existe un número entero el cual al ser multiplicado por sí mismo resulte en 50. Entonces, reescribimos esta raíz cuadrada de la siguiente manera:
$latex \sqrt{50}=\sqrt{25}\sqrt{2}$
Similar al anterior problema, podemos encontrar un número entero que resulte en 25 al ser elevado al cuadrado. Este número es 5, entonces, tenemos:
$latex \sqrt{25}\sqrt{2}=5\sqrt{2}$
EJERCICIO 5
Simplifica lo siguiente: $latex \sqrt{132}$.
Solución
El 132 es un número grande y es un poco difícil saber lo que podemos hacer. Sin embargo, podemos ver que es divisible por 2, por lo que podemos escribir:
$latex \sqrt{132}=\sqrt{66}\sqrt{2}$
También sabemos que el 66 es divisible por 2, por lo que escribimos:
$latex \sqrt{66}\sqrt{2}=\sqrt{33}\sqrt{2}\sqrt{2}$
Si es que multiplicamos la raíz cuadrada de un número por sí misma, obtenemos al número original. Entonces, tenemos:
$latex \sqrt{33}\sqrt{2}\sqrt{2}=2\sqrt{33}$
Ejercicios de raíz cuadrada para resolver
Practica lo aprendido y pon a prueba tus conocimientos con los siguientes ejercicios de raíz cuadrada. Escoge una respuesta y haz clic en “Verificar” para comprobar que seleccionaste la respuesta correcta.
Los ejercicios resueltos de arriba pueden servir de guía si tienes algún problema con estos ejercicios.
Véase también
¿Interesado en aprender más sobre expresiones algebraicas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
