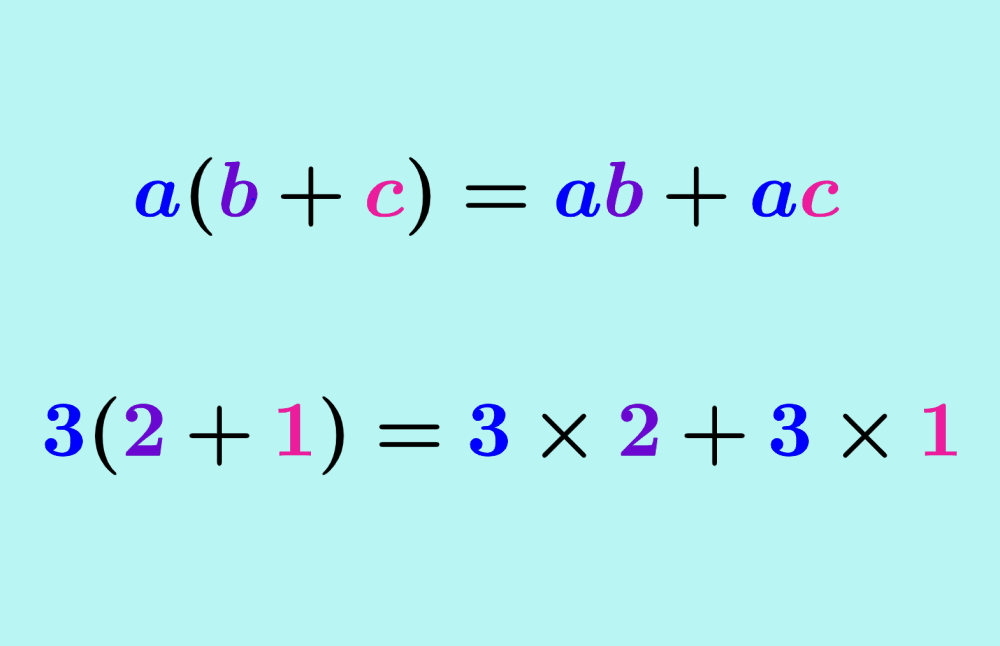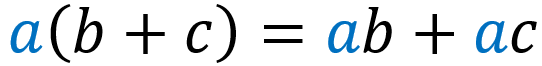La propiedad distributiva puede ser usada para simplificar expresiones algebraicas. Con la propiedad distributiva, podemos distribuir el término que está siendo multiplicado por un paréntesis.
A continuación, miraremos un resumen de la propiedad distributiva de expresiones algebraicas. Además, veremos varios ejercicios resueltos para dominar completamente este tema. También veremos ejercicios interactivos para resolver.
Resumen de la propiedad distributiva
En álgebra, usamos la propiedad distributiva para remover los paréntesis cuando simplificamos expresiones. La propiedad distributiva nos indica que podemos distribuir un término que está multiplicando a un paréntesis que contiene varios términos:
Por ejemplo, si es que queremos simplificar la expresión $latex 5(x+2)$, el orden de las operaciones nos indica que debemos resolver las operaciones dentro de los paréntesis primero. Sin embargo, no podemos sumar x y 2, ya que no son términos semejantes. Entonces, usamos la propiedad distributiva:
$latex 5(x+2)$
$latex =5(x)+5(2)$
$latex =5x+10$
También es importante recordar que, cuando simplificamos expresiones algebraicas, combinamos términos semejantes. Los términos semejantes son términos de una expresión los cuales tienen la misma variable elevada a la misma potencia.
Por ejemplo, $latex 3x$ y $latex 2x$ son términos semejantes y $latex {{x}^2}$ y $latex 5{{x}^2}$ también son términos semejantes.
10 Ejercicios resueltos de propiedad distributiva
EJERCICIO 1
Resuelve la expresión $latex 10(4+3)$ usando la propiedad distributiva.
Solución
La propiedad distributiva nos dice que tenemos que distribuir a la multiplicación por 10 a cada uno de los términos dentro del paréntesis. Entonces, tenemos:
$latex 10(4+3)$
$latex =10(4)+10(3)$
$latex =40+30$
$latex =70$
EJERCICIO 2
Encuentra el resultado de $latex 5(5-7)+3$.
Solución
Vamos a usar la propiedad distributiva para simplificar a la operación de la siguiente forma:
$latex 5(5-7)+3$
$latex =5(5)+5(-7)+3$
$latex =25-35+3$
$latex =-10+3$
$latex =-7$
EJERCICIO 3
Encuentra el resultado de $latex 5(3-4+5)$.
Solución
En este caso, tenemos una suma de tres números. Entonces, distribuimos la multiplicación por 5 a los tres números del paréntesis:
$latex 5(3-4+5)$
$latex =5(3)+5(-4)+5(5)$
$latex =15-20+25$
$latex =-5+25$
$latex =20$
EJERCICIO 4
Usa la propiedad distributiva para simplificar la expresión $latex 10(x+3)$.
Solución
Usamos la propiedad distributiva para distribuir el 10 a los términos dentro del paréntesis:
$latex 10(x)+10(3)$
Ahora multiplicamos esto y simplificamos:
$latex 10x+30$
EJERCICIO 5
Simplifica la expresión $latex 4x(2x+4)$.
Solución
Usamos la propiedad distributiva para distribuir el 4x:
$latex 4x(2x)+4x(4)$
Ahora, multiplicamos y simplificamos:
$latex 8x^2+16x$
EJERCICIO 6
Usa la propiedad distributiva para simplificar la expresión $latex 4(a+2)+2+a$
Solución
Aplicando la propiedad distributiva, podemos escribir de la siguiente forma:
$latex 4(a+2)+2+a$
$latex =4(a)+4(2)+2+a$
$latex =4a+8+2+a$
Ahora, combinamos términos semejantes:
$latex =(4a+a)+(8+2)$
$latex =5a+10$
EJERCICIO 7
Aplica la propiedad distributiva en la expresión $latex 5(5a-6)+4(2a+2)$.
Solución
Tenemos multiplicaciones por dos paréntesis. Entonces, usamos la propiedad distributiva en ambos paréntesis para obtener lo siguiente:
$latex 5(5a-6)+4(2a+2)$
$$=5(5a)+5(-6)+4(2a)+4(2)$$
$latex =25a-30+8a+8$
Ahora, combinamos términos semejantes para simplificar:
$latex =(25a+8a)+(-30+8)$
$latex =33a-22$
EJERCICIO 8
Simplifica la expresión $latex -5y(3x-3y)$.
Solución
Distribuimos el -5y a los términos dentro del paréntesis sin olvidar el cambio de signo producido por el signo menos:
$latex -5y(3x)-5y(-3y)$
Ahora solo tenemos que multiplicar y simplificar:
$latex -15xy+15y^2$
EJERCICIO 9
Usa la propiedad distributiva para simplificar $latex 4x(3x+4y+5)$.
Solución
Aquí distribuimos la multiplicación por $latex 4x$ a los tres términos dentro del paréntesis:
$latex 4x(3x)+4x(4y)+4x(5)$
Ahora multiplicamos y simplificamos:
$latex 12 x^2+16xy+20x$
EJERCICIO 10
Simplifica la expresión $latex 2x(5x^3+3x^2+5x)$.
Solución
Distribuimos el 2x a los tres términos dentro del paréntesis:
$latex 2x(5x^3)+2x(3x^2)+2x(5x)$
Multiplicamos y simplificamos:
$latex 10x^4+6x^3+10x^2$
→ Calculadora de propiedad distributiva
Ejercicios de propiedad distributiva para resolver
Usa la propiedad distributiva para simplificar la expresión $$5(a+3)-4a+6(a-2)+2a-5$$
Escribe la expresión en la casilla.
Véase también
¿Interesado en aprender más sobre propiedad distributiva y expresiones algebraicas? Mira estas páginas:
