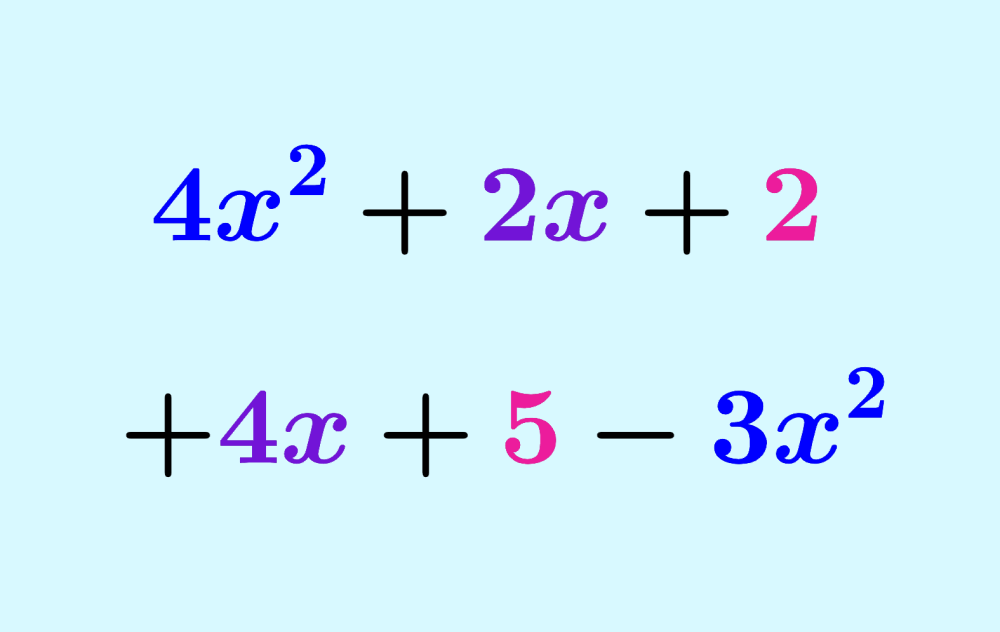Los términos semejantes son términos de expresiones algebraicas que tienen las mismas variables con las mismas potencias. Estos términos pueden ser sumados para simplificar una expresión algebraica. Los términos constantes también son considerados términos semejantes.
A continuación, veremos una definición de los términos semejantes. Luego, resolveremos algunos ejercicios de combinación de términos semejantes en expresiones algebraicas.
Definición de términos semejantes en expresiones algebraicas
Los términos semejantes son términos algebraicos que contienen las mismas variables elevadas a las mismas potencias. Estos términos pueden ser sumados para simplificar las expresiones algebraicas.
Dos o más términos semejantes pueden o no tener los mismos coeficientes. Para que dos términos sean semejantes, solo deben tener las mismas variables con los mismos exponentes.
Recordemos que las variables son las «letras» de un término algebraico y los coeficientes son los números que multiplican a las variables.
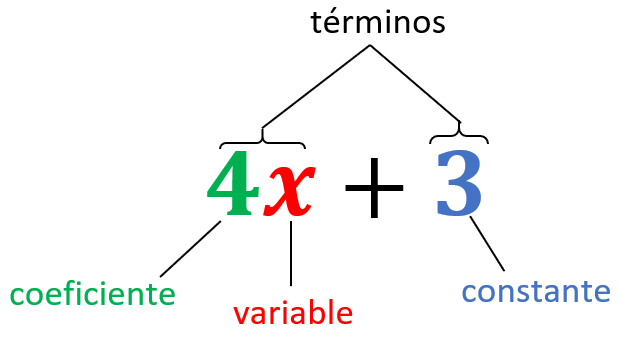
Los términos constantes, es decir, términos que no tienen variables, también son considerados términos semejantes.
Los siguientes son algunos ejemplos de términos semejantes y no semejantes:
Términos semejantes
- $latex 2x^2~$ y $latex ~4x^2$
- $latex 4x^2y~$ y $latex ~2x^2y$
- $latex x^3z~$, $latex ~4x^3z~$ y $latex ~3x^3z~$
Términos no semejantes
- $latex 2x^2~$ y $latex ~2x$
- $latex 3x^2y~$ y $latex ~2x^2$
- $latex x^2z$ ~y $latex ~4x^3z$
10 Ejercicios resueltos de términos semejantes
EJERCICIO 1
Determina los términos que son términos semejantes de $latex 6x^2$.
$latex 2x^2~~$ $latex ~~5x~~$ $latex ~~3x^3~~$ $latex ~~4x^2$
Solución
El término dado es $latex 6x^2$. Observamos que tiene una variable, x, elevada a la potencia de 2. Entonces, analizamos cada uno de los términos dados
- $latex 2x^2$ tiene la misma variable x, elevada a 2. Sí es un término semejante.
- $latex 5x$ tiene la misma variable x, pero no está elevada a 2. No es un término semejante.
- $latex 3x^3$ tiene la misma variable x, pero no está elevada a 2. No es un término semejante.
- $latex 4x^2$ tiene la misma variable x, elevada a 2. Sí es un término semejante.
Los términos semejantes de $latex 6x^2$ son $latex 2x^2~$ y $latex ~4x^2$.
EJERCICIO 2
¿Cuáles de los siguientes son términos semejantes de $latex 2xy^2$?
$latex 3xy^2~~$ $latex ~~2xy~~$ $latex ~~5xy^3~~$ $latex ~~4xz^2$
Solución
Queremos términos con $latex xy^2$. Analizando cada uno de los términos dados, tenemos:
- $latex 3xy^2$ tiene las mismas variables con los mismos exponentes. Sí es un término semejante.
- $latex 2xy$ tiene las mismas variables, pero con diferentes exponentes. No es un término semejante.
- $latex 5xy^3$ tiene las mismas variables, pero con diferentes exponentes. No es un término semejante.
- $latex 4xz^2$ no tiene las mismas variables. No es un término semejante.
El término semejante de $latex 2xy^2$ es $latex 3xy^2$.
EJERCICIO 3
Identifica a los términos semejantes de $latex -2x^2y$.
$latex 3y^2z~~$ $latex ~~-3xy^2~~$ $latex ~~4x^2y~~$ $latex ~~5x^2z$
Solución
Tenemos que encontrar términos con $latex x^2y$. Entonces, tenemos:
- $latex 3y^2z$ no tiene las mismas variables. No es un término semejante.
- $latex -3xy^2$ tiene las mismas variables, pero con exponentes diferentes. No es un término semejante.
- $latex 4x^2y$ tiene las mismas variables con los mismos exponentes. Sí es un término semejante.
- $latex 5x^2z$ no tiene las mismas variables. No es un término semejante.
El término semejante de $latex -2x^2y$ es $latex 4x^2y$.
EJERCICIO 4
¿Cuáles de los siguientes son términos semejantes de $latex 4x^2y^3z$?
$latex 3xy^2z^2~~$ $latex ~~2x^2y^3z~~$ $latex ~~4x^2y^3z^2~~$ $latex ~~-2x^2y^3w$
Solución
En este caso, tenemos que encontrar términos con $latex x^2y^3z$. Mirando cada término dado, tenemos:
- $latex 3xy^2z^2$ tiene las mismas variables, pero con diferentes exponentes. No es un término semejante.
- $latex 2x^2y^3z$ tiene las mismas variables los mismos exponentes. Sí es un término semejante.
- $latex 4x^2y^3z^2$ tiene las mismas variables, pero con diferentes exponentes. No es un término semejante.
- $latex -2x^2y^2w$ no tiene las mismas variables. No es un término semejante.
El término semejante de $latex 4x^2y^3z$ es $latex 2x^2y^3z$.
EJERCICIO 5
Combina los términos semejantes de la siguiente expresión:
$$2x^2+2x+5x+4x^2+3x+2x^2$$
Solución
Para combinar términos semejantes, podemos empezar identificando a todos los términos semejantes:
- $latex 2x^2~$, $latex ~4x^2~$ y $latex ~2x^2$
- $latex 2x~$, $latex ~5x~$ y $latex ~3x$
Ahora, sumamos estos términos y tenemos:
$$(2x^2+4x^2+2x^2)+(2x+5x+3x)$$
$$=8x^2+10x$$
EJERCICIO 6
Simplifica la siguiente expresión al combinar términos semejantes:
$$3y^2+2y+y^2+5+4y+3+2y^2+4$$
Solución
Identificando a los términos semejantes, tenemos:
- $latex 3y^2~$, $latex ~y^2~$ y $latex ~2y^2$
- $latex 2y~$ y $latex ~4y~$
- $latex 5~$, $latex ~3~$ y $latex ~4$
Sumando a los términos semejantes, tenemos:
$$(3y^2+y^2+2y^2)+(2y+4y)+(5+3+4)$$
$$=6y^2+6y+12$$
EJERCICIO 7
Combina los términos semejantes de la siguiente expresión:
$$2x^3+4x-2x^2+4x^2-5x^3+5x-3x^2$$
Solución
Tenemos los siguientes términos semejantes:
- $latex 2x^3~$, y $latex ~-5x^3$
- $latex -2x^2~$, $latex ~4x^2~$ y $latex ~-3x^2$
- $latex 4x~$ y $latex ~5x$
Al sumar estos términos, tenemos:
$$(2x^3-5x^3)+(-2x^2+4x^2-3x^2)+(4x+5x)$$
$$=-3x^3-x^2+9x$$
EJERCICIO 8
Simplifica la siguiente expresión al combinar términos semejantes:
$$2xy^2+4x^2y+3xy^2+5+4x^2y+3+2xy^2+2$$
Solución
Tenemos los siguientes términos semejantes:
- $latex 2xy^2~$, $latex ~3xy^2~$ y $latex ~2xy^2$
- $latex 4x^2y~$ y $latex ~4x^2y~$
- $latex 5~$, $latex ~3~$ y $latex ~2$
Al sumar estos términos, tenemos:
$$(2xy^2+3xy^2+2xy^2)+(4x^2y+4x^2y)+(5+3+2)$$
$$=7xy^2+8x^2y+10$$
EJERCICIO 9
Combina los términos semejantes de la siguiente expresión:
$$3ab^2-2a^2b+5ab^2-ab+3a^2b+2ab+2ab^2-a^2b$$
Solución
Vamos a empezar identificando a los términos semejantes de la expresión dada:
- $latex 3ab^2~$, $latex ~5ab^2~$ y $latex ~2ab^2$
- $latex -2a^2b~$, $latex ~3a^2b~$ y $latex ~-a^2b~$
- $latex -ab~$, y $latex ~2ab$
Sumando a los términos semejantes, tenemos:
$$(3ab^2+5ab^2+2ab^2)+(-2a^2b+3a^2b-a^2b)+(-ab+2ab)$$
$$=10ab^2+ab$$
EJERCICIO 10
Combina los términos semejantes de la siguiente expresión:
$$xyz^2-2x^2yz+5xy^2z+4x^2yz+3xy^2z-2x^2yz+2xyz^2$$
Solución
Tenemos los siguientes términos semejantes:
- $latex xyz^2~$, y $latex ~2xyz^2$
- $latex -2x^2yz~$, $latex ~4x^2yz~$, $latex -2x^2yz$
- $latex 5xy^2z~$ y $latex ~3xy^2z$
Cuando sumamos estos términos, tenemos:
$$(xyz^2+2xyz^2)+(-2x^2yz+4x^2yz-2x^2yz)+(5xy^2z+3xy^2z)$$
$$=3xyz^2+8xy^2z$$
Ejercicios de términos semejantes para resolver


¿Cuál es el coeficiente de $latex x^2y$ cuando combinamos términos semejantes? $$2xy^2+2x^2y+3x^2y-4xy^2-3x^2y-xy^2-4x^2y$$
Escribe el valor en la casilla.
Véase también
¿Interesado en aprender más sobre términos semejantes y expresiones algebraicas? Puedes mirar estas páginas: