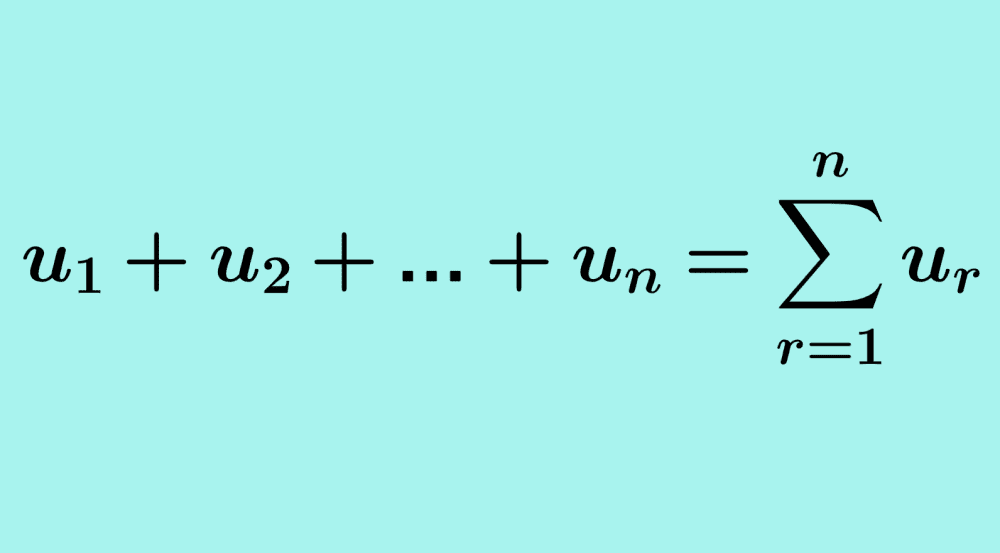Las series son las sumas de los términos de las sucesiones. Similar a las sucesiones, podemos tener series finitas o infinitas y series convergentes o divergentes. La notación sigma o las sumatorias son usadas para expresar a las series en una forma más concisa.
A continuación, veremos algunos ejercicios en los que practicaremos la relación entre las series y las sumatorias. Principalmente, veremos cómo escribir a una serie usando notación sigma.
Escribir a las series en notación sigma o sumatorias
Dado que las series son la suma de los términos de una sucesión, podemos usar notación sigma (Σ) para escribirlas.
Escribimos a la suma de los primeros $latex n $ términos de una sucesión como $latex S_{n}$, en donde
$$S_{n}=u_{1}+u_{2}+u_{3}+…+u_{n}$$
Este es un ejemplo de una serie finita, ya que hay un número finito de términos. Podemos expresar esto más concisamente de la siguiente forma:
$$u_{1}+u_{2}+u_{3}+…+u_{n}=\sum_{r=1}^{n} u_{r}$$
Para escribir a las series en notación sigma, tenemos que identificar la regla con la que cada término de la sucesión es formado. Por ejemplo, la serie finita $latex 7+11+15+19$ puede ser escrita como
$$\sum_{r=1}^{4} (4r+3)$$
Podemos ver que cada término es formado al sumar 4 al término anterior, por lo que estamos sumando múltiplos del 4 a los términos consecutivos.
La serie infinita $latex 1+4+9+16+…$ puede ser escrita como
$$\sum_{r=1}^{\infty} r^2$$
10 Ejercicios resueltos de series y sumatorias
EJERCICIO 1
Encuentra todos los términos de la serie $latex \sum_{r=1}^{5} r(r+1)$.
Solución
Podemos encontrar los términos de la serie al usar el valor de r en la expresión $latex r(r+1)$ empezando desde $latex r=1$ hasta $latex r=5$:
- Cuando $latex r=1$, tenemos $latex (1)(1+1)=2$
- Cuando $latex r=2$, tenemos $latex (2)(2+1)=6$
- Cuando $latex r=3$, tenemos $latex (3)(3+1)=12$
- Cuando $latex r=4$, tenemos $latex (4)(4+1)=20$
- Cuando $latex r=4$, tenemos $latex (5)(5+1)=30$
Entonces, los términos de la serie son $latex 2+6+12+20+30$.
EJERCICIO 2
Escribe todos los términos de la serie $latex \sum_{r=1}^{7} (\frac{(-1)^{r-1}}{r})$.
Solución
En este caso, sustituimos el valor de $latex r=1$ hasta $latex r=7$ en la expresión $latex (\frac{(-1)^{r-1}}{r})$:
- Cuando $latex r=1$, tenemos $latex (\frac{(-1)^{1-1}}{1})=1$
- Cuando $latex r=2$, tenemos $latex (\frac{(-1)^{2-1}}{2})=-\frac{1}{2}$
- Cuando $latex r=3$, tenemos $latex (\frac{(-1)^{3-1}}{3})=\frac{1}{3}$
- Cuando $latex r=4$, tenemos $latex (\frac{(-1)^{4-1}}{4})=-\frac{1}{4}$
- Cuando $latex r=5$, tenemos $latex (\frac{(-1)^{5-1}}{5})=\frac{1}{5}$
- Cuando $latex r=6$, tenemos $latex (\frac{(-1)^{6-1}}{6})=-\frac{1}{6}$
- Cuando $latex r=7$, tenemos $latex (\frac{(-1)^{7-1}}{7})=\frac{1}{7}$
Entonces, los términos de la serie son
$$1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\frac{1}{6}+\frac{1}{7}$$
EJERCICIO 3
¿Cuál es la suma de los primeros cuatro términos de la siguiente sucesión?
$latex u_{r}=(-1)^r~3^{r+1}$ para $latex r\geq 1$
Solución
Esta es una serie escrita como $latex S_{4}$, que es la suma de los primeros cuatro términos. Usando sumatorias, tenemos:
$$S_{4}=\sum_{r=1}^{4}(-1)^r~3^{r+1}$$
$$=(-1)3^2+(-1)^23^3+(-1)^33^4+(-1)^43^5$$
$latex =-3^2+3^3-3^4+3^5$
$latex S_{4}=180$
La suma de los primeros cuatro términos es igual a 180.
EJERCICIO 4
Representa a la siguiente serie usando notación sigma:
$$\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+…+\frac{1}{20}$$
Solución
Esta serie puede ser formada usando la expresión $latex \frac{1}{r}$, en donde r incrementa por 1 en cada término consecutivo.
Además, podemos observar que la serie empieza en $latex r=3$ y termina en $latex r=20$. Entonces, la escribimos de la siguiente forma:
$$\sum_{r=3}^{20}\frac{1}{r}$$
EJERCICIO 5
Representa a la siguiente serie usando notación sigma:
$$-1+2+7+14+23$$
Solución
Tal vez no podamos identificar al patrón de la serie a primera vista. Sin embargo, podemos considerar una serie en la que sus términos son definidos por $latex u_{r}=r^2$:
$latex 1+4+9+16+25$
Comparando esta serie con la serie dada, observamos que si restamos 2 a cada término de la serie definida, obtenemos la serie requerida. Entonces, tenemos la expresión $latex u_{r}=r^2-2$.
Usando notación sigma, tenemos:
$$\sum_{r=1}^{5}(r^2-2)$$
EJERCICIO 6
Usa notación sigma para escribir a la siguiente serie:
$$6-7+8-9+…$$
Solución
Esta es una serie infinita, ya que está indicado que la serie continúa indefinidamente.
Si es que ignoramos el signo negativo, vemos que cada término incrementa por 1. Entonces, el término r de la serie $latex 6+7+8+9+…$ está dado por $latex u_{r}=r+5$.
Ahora, podemos multiplicar por $latex (-1)^{r-1}$, ya que esta expresión nos da el signo alternante. Entonces, tenemos:
$latex u_{r}=(-1)^{r-1}(r+5)$
Cuando $latex (r+1)$ es par, el signo es positivo y cuando $latex (r+1)$ es impar, el signo es negativo.
Por lo tanto, en notación sigma, tenemos:
$$\sum_{r=1}^{\infty}(-1)^{r+1}(r+5)$$
En este caso, también es posible escribir a la serie de la siguiente forma:
$$\sum_{r=5}^{\infty}(-1)^{r+1}(r+1)$$
EJERCICIO 7
Escribe a la siguiente serie en notación sigma:
$$4-8+16-32+64-128+256-512+1024$$
Solución
Similar al ejercicio anterior, aquí también tenemos un signo negativo alternante. Entonces, podemos implementar esto usando la expresión $latex (-1)^{r+1}$.
Si es que ignoramos el signo negativo, vemos que los términos son formados por potencias del 2. Es decir, tenemos $latex 2^2+2^3+2^4+…$.
Entonces, los términos son hallados con la expresión $latex (2)^{r+1}$ empezando desde $latex r=1$ hasta $latex r=9$. Por lo tanto, en notación sigma, tenemos:
$$\sum_{r=1}^{9}(-2){r+1}$$
EJERCICIO 8
Escribe a la siguiente serie en notación sigma:
$$\frac{5}{5^2-1}+\frac{6}{6^2-1}+\frac{7}{7^2-1}+…+\frac{n}{n^2-1}$$
Solución
Los términos de esta serie son formados usando la expresión $latex \frac{r}{r^2-1}$, en donde r incrementa por 1 en cada término consecutivo.
En este caso, los límites van desde $latex r=5$ hasta $latex r=n$. Entonces, usando notación sigma, tenemos:
$$\sum_{r=5}^{n}\frac{r}{r^2-1}$$
EJERCICIO 9
Escribe a la siguiente serie en notación sigma:
$$\frac{1}{2\times 3}+\frac{2}{3\times 4}+\frac{3}{4\times 5}+…+\frac{n}{(n+1)(n+2)}$$
Solución
Este ejercicio es similar al anterior, ya que podemos usar el último término dado para obtener la expresión de la sumatoria fácilmente. Es decir, tenemos $latex \frac{r}{(r+1)(r+2)}$
Además, observamos que la serie va desde $latex r=1$ hasta $latex r=n$. Entonces, la escribimos de la siguiente forma:
$$\sum_{r=1}^{n}\frac{n}{(n+1)(n+2)}$$
EJERCICIO 10
Escribe a la siguiente serie en notación sigma:
$$1\times 4-3\times 7 +5 \times 10-…+29\times 46$$
Solución
Primero, observamos que la serie tiene signos negativos alternantes, por lo que sabemos que vamos a usar la expresión $latex (-1)^{r+1}$ para implementar esto.
Luego, vemos que cada término es una multiplicación de dos números. Entonces, buscamos una expresión para cada parte en términos de r.
La primera parte puede ser obtenida usando $latex (2r-1)$ y la segunda parte puede ser obtenida con $latex (3r+1)$.
Por último, observamos que la serie va desde $latex r=1$ hasta $latex r=15$. Entonces, combinando todo esto, tenemos:
$$\sum_{r=1}^{15}(-1)^{r+1}(2r-1)(3r+1)$$
Ejercicios de series y sumatorias para resolver
Véase también
¿Interesado en aprender más sobre series y sucesiones? Puedes mirar estas páginas: