La sección transversal representa a la intersección de un plano con un objeto tridimensional. La sección transversal es la figura bidimensional obtenida por la intersección de un plano con una figura tridimensional. Por ejemplo, cuando un cilindro es cortado por un plano que es paralelo a una de sus bases, la sección transversal obtenida es un círculo. Dependiendo de la orientación del plano, podemos obtener varias secciones transversales del mismo objeto.
A continuación, conoceremos más detalles sobre las secciones transversales y exploraremos las secciones transversales de las figuras más importantes.
GEOMETRÍA
Relevante para…
Aprender sobre las secciones transversales de figuras geométricas.
GEOMETRÍA
Relevante para…
Aprender sobre las secciones transversales de figuras geométricas.
Tipos de secciones transversales
Dependiendo de la orientación del plano que corta al objeto, podemos tener tres tipos de secciones transversales:
- Sección transversal horizontal
- Sección transversal vertical
- Sección transversal inclinada
Sección transversal horizontal o paralela
Esta sección transversal es formada cuando un plano corta a un objeto en una dirección paralela a la base del objeto.
Sección transversal vertical o perpendicular
Una sección transversal vertical es formada cuando un objeto es cortado por un plano perpendicular a su base, es decir, con un ángulo de 90°.
Sección transversal inclinada
Esta sección transversal es formada cuando el ángulo de inclinación del plano que corta al objeto es mayor que 0° y menor que 90°.
Área de la sección transversal
Cuando un plano corta a un objeto sólido, un área es proyectada en el plano. Si es que el plano está orientado horizontalmente, será perpendicular al eje de simetría. Dependiendo de la figura, podemos calcular el área de la sección transversal al reconocer que la sección transversal es igual a las bases de la figura.
EJEMPLO
Encuentra el área de la sección transversal de un plano paralelo a la base de un cubo que tiene un volumen igual a 125 m³.
Solución: Podemos reconocer que el área de la sección transversal será igual al área de una de las caras del cubo, ya que el plano es paralelo a las bases. Entonces, tenemos que encontrar el área de una cara del cubo.
El volumen del cubo es igual a $latex V={{a}^3}$, en donde, a es la longitud de un lado del cubo. Esto significa que la longitud de un lado es $latex a=5$.
Ahora, sabemos que el área de un cuadrado es $latex A={{a}^2}$, por lo que el área de la sección transversal es $latex A=25$.
Secciones transversales del cubo
Un cubo es una figura tridimensional que tiene todos sus lados con la misma longitud. Un cubo tiene un total de seis caras cuadradas. Esto significa que, cuando un plano corta a un cubo en una dirección que es paralela a una de sus caras, la sección transversal siempre será un cuadrado.
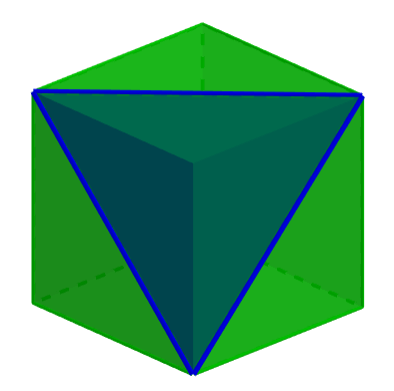
Sin embargo, también es posible obtener diferentes secciones transversales al cortar al cubo con una inclinación con respecto a su base. Si es que el plano interseca a tres aristas del cubo, su sección transversal será un triángulo.
Si es que el plano que corta corta al cubo en una forma en la que cruze por las diagonales de las caras, obtendremos una sección transversal rectangular:
Adicionalmente, también podemos formar una sección transversal hexagonal al intersecar al cubo con un plano inclinado de la siguiente manera:
Secciones transversales del cilindro
Un cilindro es una figura 3D que tiene bases circulares, las cuales son conectadas por una superficie lateral. Dependiendo en cómo sea cortado, las secciones transversales del cilindro pueden ser un círculo, un rectángulo o un óvalo.
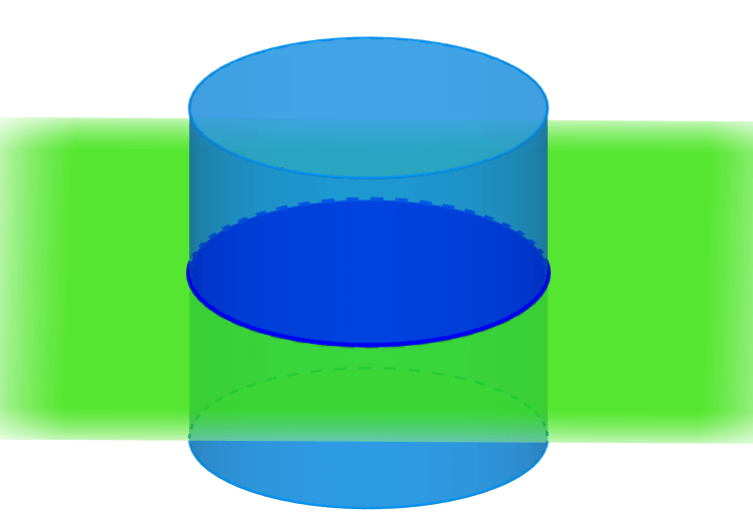
Si es que el cilindro es cortado con un plano paralelo a una de sus bases, la sección transversal será un círculo.
La sección transversal óvala es obtenida cuando el plano corta al cilindro con un ángulo mayor que 0° y menor que 90° con respecto a la base.
Si es que el plano corta al cilindro en una dirección perpendicular a las bases, la sección transversal será un rectángulo.
Secciones transversales del cono
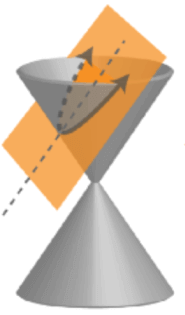
Un cono puede ser considerado como una pirámide con una sección transversal circular. Dependiendo de la relación entre el plano y la superficie cortada, las secciones transversales de un cono pueden ser círculos, elipses, parábolas e hipérbolas.
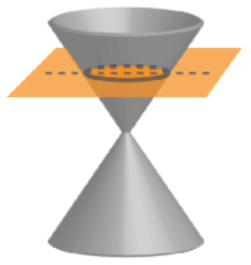
Un círculo es formado cuando un cono es cortado por un plano que es paralelo a su base.
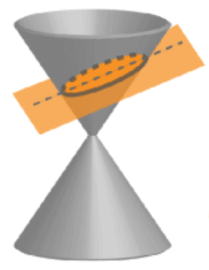
Una elipse es formada cuando un cono es cortado por un plano que es inclinado con un ángulo pequeño (menor que el ángulo de los lados laterales) con respecto a la base del cono.
Una parábola es formada cuando el plano que corta al cono es paralelo a un lado lateral del cono.
Una hipérbola es formada cuando el plano que corta al cono tiene un ángulo superior (mayor que el ángulo de los lados laterales) con respecto a la base del cono.
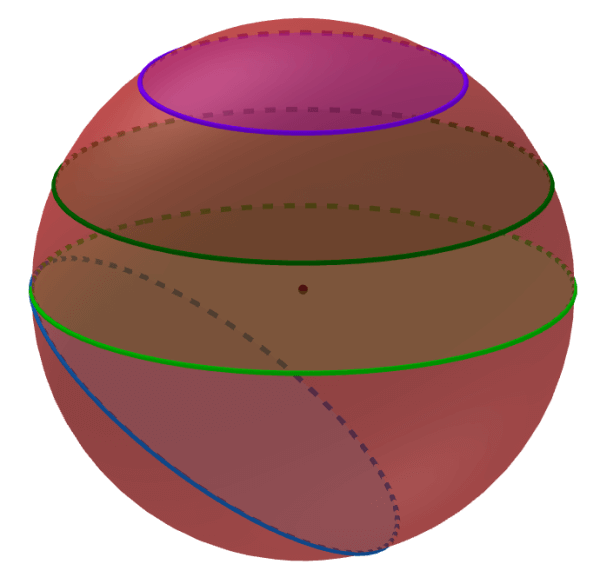
Secciones transversales de la esfera
Una esfera es una figura tridimensional perfectamente redonda. La sección transversal de una esfera siempre es un círculo sin importar la orientación del plano.
Véase también
¿Interesado en aprender más sobre figuras geométricas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
