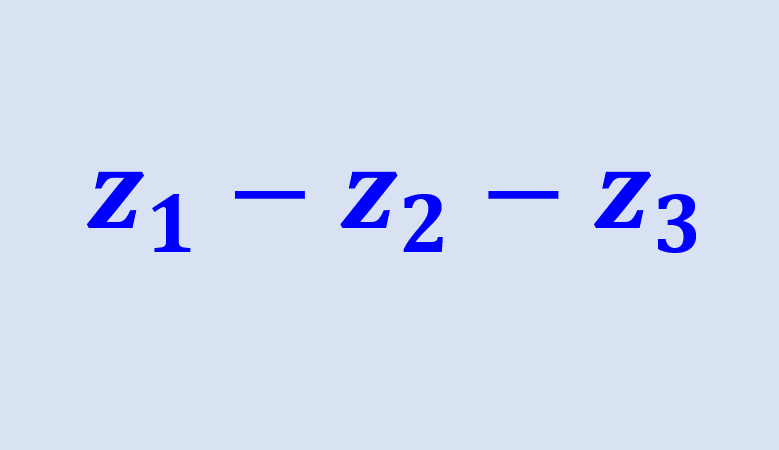Los números complejos son escritos en la forma general a+bi, en donde a y b son números reales y “i” es la unidad imaginaria que es igual a la raíz cuadrada de menos uno. Las operaciones básicas como suma, resta, multiplicación y división pueden ser realizadas con números complejos. La idea principal al realizar operaciones con números complejos es separar sus partes real e imaginaria.
A continuación, aprenderemos cómo resolver restas de números complejos. Además, veremos varios ejercicios resueltos para dominar este tema completamente.
¿Cómo resolver restas de números complejos?
Para resolver restas de números complejos, tenemos que identificar sus partes real e imaginaria y restarlas separadamente. Esto es muy parecido a restar polinomios, en donde identificamos y restamos los términos semejantes.
Entonces, suponiendo que tenemos los números complejos $latex z_{1}=a+bi$ y $latex z_{2}=c+di$, su resta es igual a:
| $latex z_{1}-z_{2}=(a-c)+(b-d)i$ |
Podemos observar que la parte real del resultado es igual a la resta de las partes reales de los números originales y la parte imaginaria del resultado es igual a la resta de las partes imaginarias de los números originales. Esto significa que tenemos:
$latex Re(z_{1}-z_{2})=Re(z_{1})-Re(z_{2})$
$latex Im(z_{1}-z_{2})=Im(z_{1})-Re(z_{2})$
Podemos restar cualquier cantidad de números complejos siguiendo esta regla simple.
Ejercicios de restas de números complejos resueltos
Con los siguientes ejercicios, puedes aplicar lo aprendido sobre restas de números complejos. Cada ejercicio tiene su respectiva solución, pero es recomendable que intentes resolver los ejercicios tú mismo antes de mirar la respuesta.
EJERCICIO 1
Si es que tenemos los números $latex z_{1}=4+5i$ y $latex z_{2}=3+6i$, ¿cuál es el resultado de $latex z_{1}-z_{2}$?
Solución
Identificamos a las partes real e imaginaria de los números y las restamos separadamente. Entonces, tenemos:
$latex z_{1}-z_{2}=(4-3)+(5-6)i$
$latex =1-i$
EJERCICIO 2
Si es que tenemos los números $latex z_{1}=6+8i$ y $latex z_{2}=5-7i$, ¿cuál es el resultado de $latex z_{1}-z_{2}$?
Solución
Identificamos a las partes real e imaginaria de los números y las restamos separadamente. Entonces, tenemos:
$latex z_{1}-z_{2}=(6-5)+(8-(-7))i$
$latex =1+15i$
EJERCICIO 3
Resuelve la resta $latex z_{1}-z_{2}-z_{3}$ si es que tenemos los números $latex z_{1}=3+6$, $latex z_{2}=4-5$ y $latex z_{3}=-2+7$.
Solución
Aquí, tenemos tres números, pero el proceso a seguir es el mismo. Agrupamos a las partes reales e imaginarias y las restamos separadamente:
$latex z_{1}-z_{2}-z_{3}=(3-4-(-2))$ $latex +(6-(-5)-7)i$
$latex =1+4i$
EJERCICIO 4
Resuelve la resta $latex z_{1}-z_{2}-z_{3}$ si es que tenemos los números $latex z_{1}=10-8$, $latex z_{2}=-6+7$ y $latex z_{3}=3-10$.
Solución
Similar al ejercicio anterior, simplemente tenemos que grupar a las partes reales e imaginarias y las restamos separadamente:
$latex z_{1}-z_{2}-z_{3}=(10-(-6)-3)$ $latex +(-8-7-(-10))i$
$latex =13-5i$
EJERCICIO 5
Si tenemos los números complejos $latex z_{1}=a+8i$, $latex z_{2}=-5+bi$ y $latex z_{3}=10+5i$, ¿cuál es el valor de a y b si es que $latex z_{3}=z_{1}-z_{2}$?
Solución
Si es que restamos a las partes reales e imaginarias de los números $latex z_{1}$ y $latex z_{2}$ separadamente, tenemos:
$latex 10=a-(-5)$
⇒ $latex a=5$
$latex 5=8-b$
⇒ $latex b=3$
EJERCICIO 6
Si tenemos los números complejos $latex z_{1}=a-6i$, $latex z_{2}=7+bi$ y $latex z_{3}=-5-10i$, ¿cuál es el valor de a y b si es que $latex z_{3}=z_{1}-z_{2}$?
Solución
Si es que restamos a las partes reales e imaginarias de los números $latex z_{1}$ y $latex z_{2}$ separadamente, tenemos:
$latex -5=a-7$
⇒ $latex a=2$
$latex -10=-6-b$
⇒ $latex b=4$
Ejercicios de restas de números complejos para resolver
Pon en práctica lo aprendido para resolver los siguientes ejercicios de restas de números complejos. Resuelve las restas y selecciona tu respuesta. Haz clic en “Verificar” para comprobar que obtuviste la respuesta correcta.
Véase también
¿Interesado en aprender más sobre operaciones con números complejos? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
