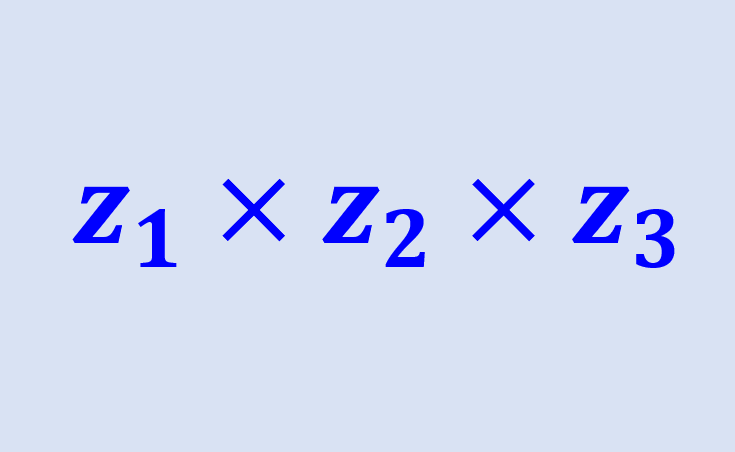Los ejercicios de multiplicación de números complejos pueden ser resueltos usando el método de distribución de la multiplicación, similar al usado para multiplicar a dos binomios. La diferencia es que, cuando tenemos a la unidad unitaria elevada al cuadrado, i², tenemos que recordar que esto es igual a -1.
A continuación aprenderemos a multiplicar números complejos. Miraremos varios ejercicios resueltos para entender cómo usar el método de multiplicación mencionado.
¿Cómo resolver multiplicaciones de números complejos?
Las multiplicaciones de números complejos son resueltas empleando un método muy similar a cuando multiplicamos dos binomios. La única diferencia es la introducción de la unidad imaginaria:
$latex \sqrt{-1}=i$
Algo importante que debemos tener en cuenta es que, cuando elevamos al cuadrado a la unidad imaginaria, tenemos:
$latex {{(\sqrt{-1})}^2}={{(i)}^2}$
$latex -1={{i}^2}$
Por ejemplo, si es que tenemos la multiplicación de los números complejos $latex z_{1}=a+bi$ y $latex z_{2}=c+di$, podemos obtener su producto de la siguiente manera:
$latex z_{1}z_{2}=(a+bi)(c+di)$
$latex =ac+adi+cbi+bd{{i}^2}$
$latex =ac+(ad+cb)i+bd(-1)$
$latex =ac+(ad+cb)i-bd$
Ejercicios de multiplicación de números complejos resueltos
El proceso de resolución mencionado arriba es usado para resolver los siguientes ejercicios de multiplicación de números complejos. Es recomendable que intentes resolver los ejercicios tú mismo antes de mirar la solución.
EJERCICIO 1
Encuentra el producto de los números complejos $latex (4+2i)(2+3i)$.
Solución
Esto es similar a multiplicar dos binomios. Expandimos la multiplicación y luego combinamos términos semejantes:
$latex (4+2i)(2+3i)$
$$=(4)(2)+(4)(3i)+(2i)(2)+(2i)(3i)$$
$latex =8+12i+4i+6{{i}^2}$
$latex =8+16i+6{{i}^2}$
Ahora, tenemos que reemplazar a $latex {{i}^2}$ por $latex -1$ y combinar términos semejantes nuevamente:
$latex =8+16i+6(-1)$
$latex =8+16i-6$
$latex =2+16i$
EJERCICIO 2
¿Cuál es el producto de $latex (4-5i)(2-7i)$?
Solución
Tenemos que expandir la multiplicación y luego combinar términos semejantes:
$latex (4-5i)(2-7i)$
$$=(4)(2)+(4)(-7i)+(-5i)(2)+(-5i)(-7i)$$
$latex =8-28i-10i+35{{i}^2}$
$latex =8-38i+35{{i}^2}$
Reconocemos que $latex {{i}^2}$ es igual a $latex -1$ y combinamos términos semejantes nuevamente:
$latex =8-38i+35(-1)$
$latex =8-38i-35$
$latex =-27-38i$
EJERCICIO 3
Si es que tenemos $latex z_{1}=6-5i$ y $latex z_{2}=-4+7i$, ¿cuál es el resultado de $latex z_{1}z_{2}$?
Solución
Formamos la multiplicación, la expandimos y luego combinamos términos semejantes:
$latex (6-5i)(-4+7i)$
$$=(6)(-4)+(6)(7i)+(-5i)(-4)+(-5i)(7i)$$
$latex =-24+42i+20i-35{{i}^2}$
$latex =-24+62i-35{{i}^2}$
Reconocemos que $latex {{i}^2}$ es igual a $latex -1$ y combinamos términos semejantes nuevamente:
$latex =-24+62i-35(-1)$
$latex =-24+62i+35$
$latex =11+62i$
EJERCICIO 4
Encuentra el producto del siguiente número complejo y su conjugado: $latex 4-3i$.
Solución
El conjugado de un número complejo es encontrado al cambiar el signo del componente imaginario. En este caso, el conjugado de $latex 4-3i$ es $latex 4+3i$. Ahora, podemos multiplicarlos para obtener el producto:
$latex (4-3i)(4+3i)$
$$=(4)(4)+(4)(3i)+(-3i)(4)+(-3i)(3i)$$
$latex =16+12i-12i-9{{i}^2}$
$latex =16-9{{i}^2}$
Reemplazando a $latex {{i}^2}$ por $latex -1$ y combinando términos semejantes, tenemos:
$latex =16-9(-1)$
$latex =16+9$
$latex =25$
EJERCICIO 5
Multiplica al número $latex -1-i$ por sí mismo.
Solución
Multiplicando al número por sí mismo, tenemos:
$latex (-1-i)(-1-i)$
$$=(-1)(-1)+(-1)(-i)+(-i)(-1)+(-i)(-i)$$
$latex =1+i+i+{{i}^2}$
$latex =1+2i+{{i}^2}$
Reemplazando a $latex {{i}^2}$ por $latex -1$ y combinando términos semejantes, tenemos:
$latex =1+2i+(-1)$
$latex =2i$
EJERCICIO 6
Resuelve la multiplicación $latex (3i-5{{i}^2})(5i+4{{i}^2})$.
Solución
En este caso, tenemos una expresión con $latex {{i}^2}$, por lo que podemos empezar simplificando al reemplazar a $latex {{i}^2}$ con $latex -1$. Entonces, tenemos:
$latex (3i-5{{i}^2})(5i+4{{i}^2})$
$latex =(3i-5(-1))(5i+4(-1))$
$latex =(3i+5)(5i-4)$
$$=(3i)(5i)+(3i)(-4)+(5)(5i)+(5)(-4)$$
$latex =15{{i}^2}-12i+25i-20$
$latex =15{{i}^2}+13i-20$
Nuevamente, reemplazamos a $latex {{i}^2}$ con $latex -1$ y combinamos términos semejantes:
$latex =15(-1)+13i-20$
$latex =-15+13i-20$
$latex =-35+13i$
Ejercicios de multiplicación de números complejos para resolver
Pon en práctica tu conocimiento sobre la multiplicación de números complejos y resuelve los siguientes ejercicios. Selecciona una respuesta y verifícala para comprobar que seleccionaste la correcta. Si necesitas ayuda, puedes mirar los ejercicios resueltos de arriba.
Véase también
¿Interesado en aprender más sobre operaciones con números complejos? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
