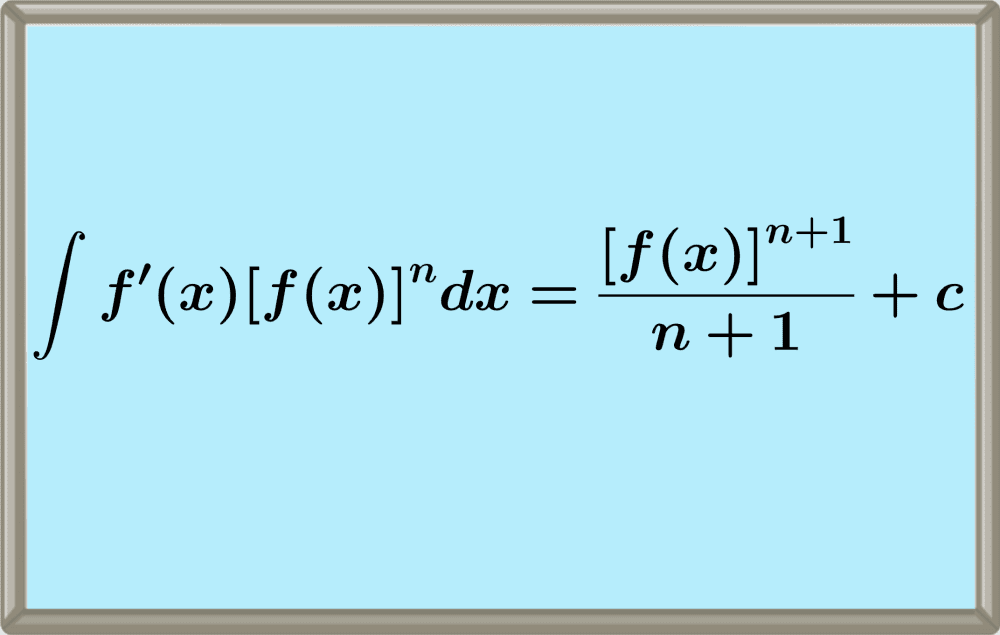La regla de la cadena para integrales es una regla de integración obtenida a partir de la regla de la cadena de derivadas. Esta regla es usada para integrar funciones de la forma f'(x)[f(x)]n.
A continuación, conoceremos cómo encontrar integrales de funciones usando la regla de la cadena para integrales. Luego, veremos algunos ejemplos en donde aplicaremos esta regla.
Fórmula de la regla de la cadena de integrales
La fórmula de la regla de la cadena de integrales es la siguiente:
$$\int f'(x)[f(x)]^ndx=\frac{[f(x)]^{n+1}}{n+1}+c$$
Podemos entender esta fórmula al considerar a la función $latex f(x)=(x^2+1)^4$. Usando la regla de la cadena de derivadas, encontramos que su derivada es:
$latex f'(x)=8x(x^2+1)^3$
Esto significa que podemos escribir de la siguiente forma:
$$\int 8x(x^2+1)^3dx=(x^2+1)^4+c$$
Ahora, podemos reconocer que el integrando $latex 8x(x^2+1)^3$ es de la forma $latex f'(x)[f(x)]^n$.
En este ejemplo tenemos $latex f(x)=x^2+1$, $latex f'(x)=2x$ y $latex n=3$.
Para mirar otro ejemplo, consideremos a la integral $latex \int x(3x^2-2)^5dx$. En este caso, observamos que la derivada de $latex (3x^2-2)$ es $latex 6x$. Además, tenemos el término $latex x$ fuera de la función principal $latex (3x^2-2)^5$.
Esto significa que consideramos a $latex (3x^2-2)^6$, lo cual al ser diferenciado nos da $latex 36x(3x^2-2)^5$. Entonces, tenemos:
$$\int x(3x^2-2)^5=\frac{1}{36}(3x^2-2)^6+c$$
Ejercicios resueltos de la regla de la cadena de integrales
EJERCICIO 1
Encuentra la siguiente integral:
$$\int (x-2)^2dx$$
Solución
Para encontrar la integral $latex \int (x-2)^2dx$, podemos considerar a la función $latex f(x)=(x-2)^3$, la cual al ser derivada nos da $latex f'(x)=3(x-2)^2$.
Esto significa que la integral de $latex (x-2)^2$ es igual a:
$$\int (x-2)^2dx=\frac{(x-2)^3}{3}+c$$
EJERCICIO 2
Resuelve la siguiente integral:
$$\int x(3x^2+6)^4dx$$
Solución
Podemos observar que la derivada de $latex 3x^2+6$ es $latex 6x$ y tenemos al término $latex x$ fuera de la función principal $latex (3x^2+6)^4$.
Esto significa podemos considerar que la derivada de $latex (3x^2+6)^5$ es $latex 30x(3x^2+6)^4$.
Entonces, tenemos la siguiente integral:
$$\int x(3x^2+6)^4dx=\frac{(3x^2+6)^5}{30}+c$$
EJERCICIO 3
Encuentra la siguiente integral:
$$\int 4x^2(x^3-3)^5dx$$
Solución
Para resolver esta integral, observamos que la derivada de $latex x^3-3$ es $latex 3x^2$.
Además, tenemos un término $latex x^2$ fuera de la función principal $latex (x^3-3)^5$.
Entonces, consideramos que la derivada de $latex (x^3-3)^6$ es $latex 18x^2(x^3-3)^5$. Entonces, tenemos:
$$\int 4x^2(x^3-3)^5dx=\frac{4}{18}(x^3-3)^6+c$$
$$=\frac{2}{9}(x^3-3)^6+c$$
EJERCICIO 4
¿Cuál es el resultado de la siguiente integral?
$$\int (x+2)(x^2+4x-1)^3dx $$
Solución
Empezamos observando que la derivada de $latex x^2+4x-1$ es $latex 2x+4=2(x+2)$.
Además, vemos que tenemos el término $latex (x+2)$ fuera de la función principal.
Luego, al considerar que la derivada de $latex (x^2+4x-1)^4$ es
$$ 4(2x+4)(x^2+4x-1)^3=8(x+2)(x^2+4x-1)^3$$
Entonces, tenemos:
$$ \int (x+2)(x^2+4x-1)^3dx=\frac{1}{8}(x^2+4x-1)^4+c $$$$ =\frac{x(x^2-4)}{x^2-25} $$
EJERCICIO 5
Encuentra la siguiente integral:
$$ \int \frac{4x}{(3-x^2)^2}dx$$
Solución
En este caso, podemos empezar escribiendo a la expresión de la siguiente forma para facilitar su resolución:
$$ \int \frac{4x}{(3-x^2)^2}dx=\int 4x (3-x^2)^{-2}$$
Ahora, podemos observar que la derivada de $latex 3-x^2$ es $latex -2x$. Además, tenemos un término $latex x$ fuera de la función principal.
Entonces, consideramos que la derivada de $latex (3-x^2)^{-1}$ es $latex 2x(3-x^2)^{-2}$.
Esto significa que esta integral es resuelta de la siguiente forma:
$$ \int \frac{4x}{(3-x^2)^2}dx=\frac{4}{2}(3-x^2)^{-1}+c $$
$$ =\frac{2}{3-x^2}+c $$
EJERCICIO 6
¿Cuál es el resultado de la siguiente integral?
$$ \int \frac{x}{\sqrt{x^2+3}}dx$$
Solución
Escribimos a la expresión de la siguiente forma:
$$ \int \frac{x}{\sqrt{x^2+3}}dx=\int x (x^2+3)^{-\frac{1}{2}}$$
Ahora, vemos que la derivada de $latex x^2+3$ es $latex 2x$ y tenemos un término $latex x$ fuera de la función principal.
Entonces, podemos resolver esto al considerar que la derivada de $latex (x^2+3)^{-\frac{1}{2}}$ es:
$$2x\times \frac{1}{2} (x^2+3)^{-\frac{1}{2}}=x(x^2+3)^{-\frac{1}{2}}$$
Esto significa que esta integral es resuelta de la siguiente forma:
$$ \int \frac{x}{\sqrt{x^2+3}}dx=(x^2+3)^{\frac{1}{2}}+c $$
$$ =\sqrt{x^2+3}+c $$
Regla de la cadena de integrales – Ejercicios para resolver
Al resolver la siguiente integral, el resultado puede ser expresado como fracción. ¿Cuál es el numerador? $$\int \frac{25x^4}{(3-x^5)^2}dx$$
Escribe el numerador en la casilla.
Véase también
¿Interesado en aprender más sobre integrales? Puedes mirar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
