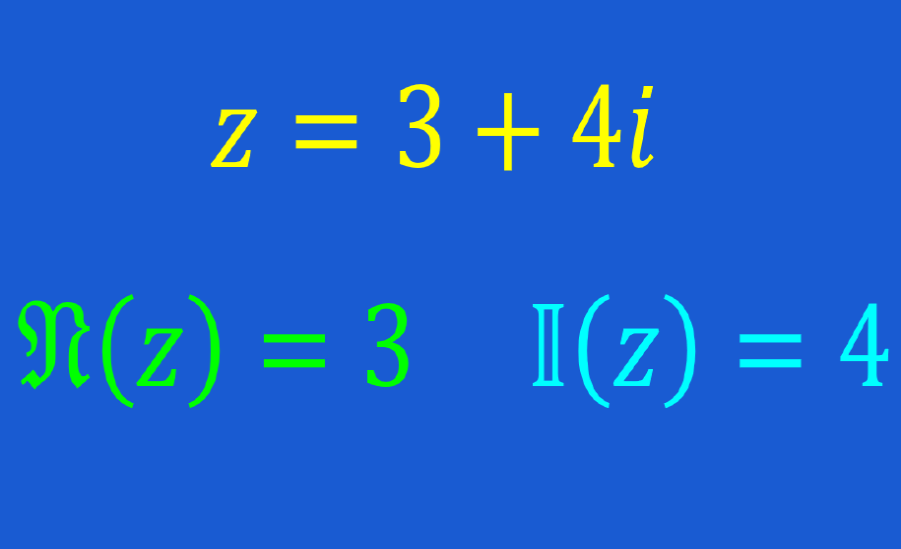Los números complejos son los números que son expresados en la forma a+bi, en donde a y b son números reales e “i” es la unidad imaginaria. El valor de la unidad imaginaria es la raíz cuadrada de menos uno, i=(√-1).
Por ejemplo, 5+3i es un número complejo, en donde 5 es un número real (Re) y 3i es un número imaginario (Im).
Ejemplos de números complejos
Los números complejos tienen la forma general $latex a+bi$, en donde, a es la parte real del número y bi es la parte imaginaria:
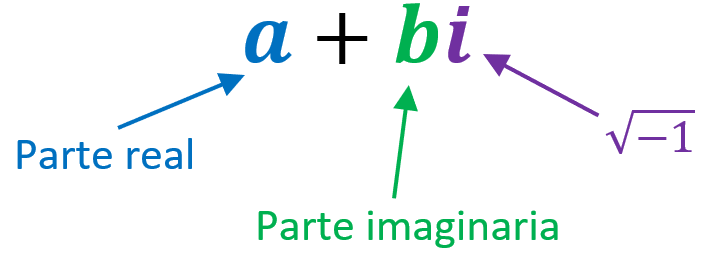
EJEMPLOS
Los números complejos son representados con la letra z:
- En el número complejo $latex z=3+7i$, 3 es la parte real y 7i es la parte imaginaria.
- En el número complejo $latex z=-6+\frac{1}{2}i$, -6 es la parte real y $latex \frac{1}{2}i$ es la parte imaginaria.
- En el número complejo $latex z=\frac{3}{4}-4i$, $latex \frac{3}{4}$ es la parte real y -4i es la parte imaginaria.
- En el número complejo $latex z=-\sqrt{3}+\sqrt{7}i$, $latex -\sqrt{3}$ es la parte real y $latex \sqrt{7}i$ es la parte imaginaria.
Propiedades de los números complejos
Las siguientes son algunas de las propiedades más importantes de los números complejos:
- Los números complejos obedecen la propiedad conmutativa de la adición y la multiplicación:
$latex z_{1}+z_{2}=z_{2}+z_{1}$
$latex z_{1}\times z_{2}=z_{2}\times z_{1}$
- Los números complejos obedecen la propiedad asociativa de la adición y la multiplicación:
$latex (z_{1}+z_{2})+z_{3}=z_{1}+(z_{2}+z_{3})$
$latex (z_{1}\times z_{2}) \times z_{3}=z_{1}( z_{2} \times z_{3})$
- Los números complejos obedecen la propiedad distributiva:
$latex z_{1}(z_{2})+z_{3})=z_{1}\times z_{2}+z_{1}\times z_{3}$
- La adición de dos números conjugados complejos resultará en un número real.
- La multiplicación de dos números conjugados complejos también resultará en un número real.
- Si es que x y y son números reales y tenemos $latex x+yi=0$, entonces, $latex x=0$ y $latex y=0$.
¿Cómo graficar números complejos?
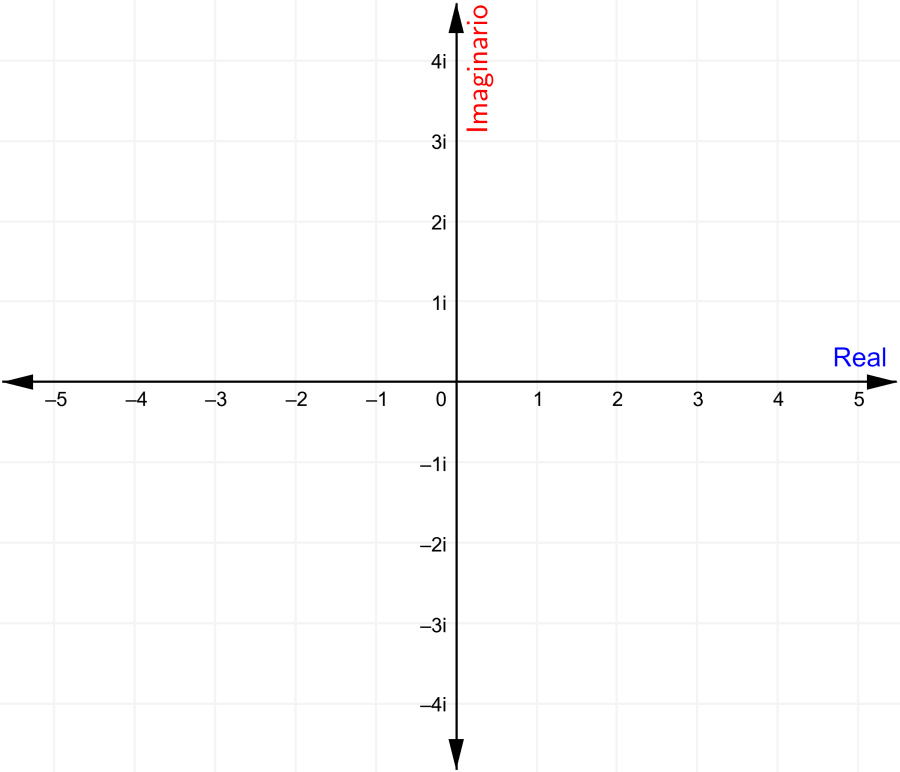
Podemos graficar a los números complejos usando el plano complejo. En este plano, el eje x representa a la parte real y el eje y representa a la parte imaginaria:
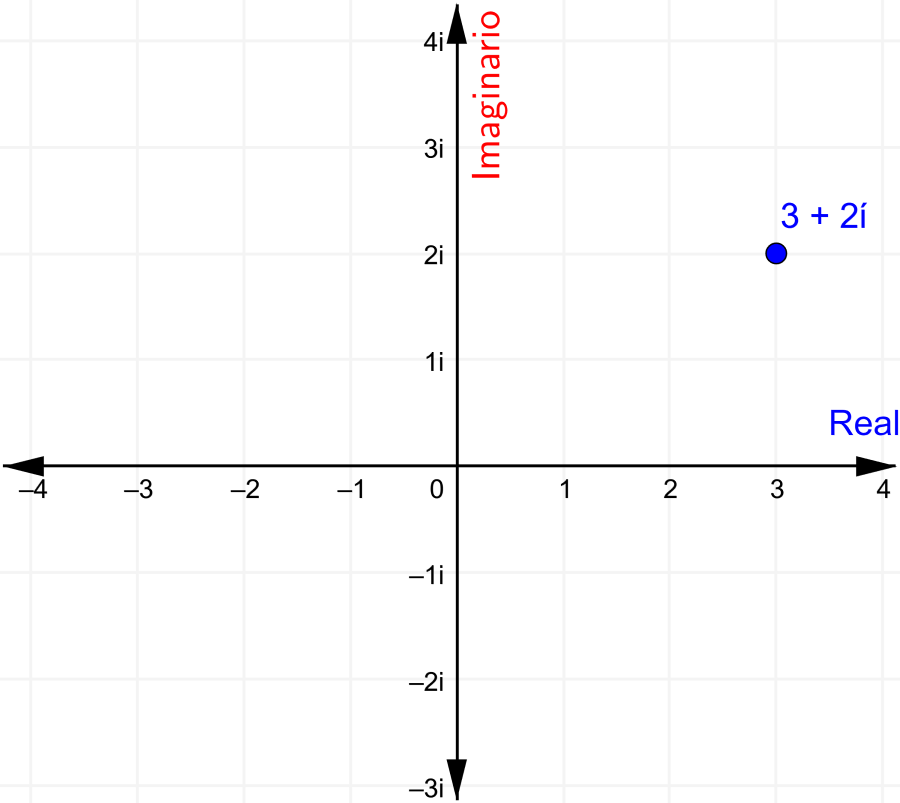
Graficar números complejos es muy fácil, solo tenemos que ubicar a cada coordenada separadamente. Por ejemplo, si tenemos que graficar al número $latex z=3+2i$, nos movemos 3 unidades en el eje real (el eje x) y 2 unidades en el eje imaginario (el eje y):
¿Para qué sirven los números complejos?
Los números complejos tienen muchas aplicaciones en la vida real, sobre todo en campos de la ingeniería, tales como electricidad. Los números complejos también son usados para encontrar soluciones a ecuaciones cuadráticas. Cuando las ecuaciones no tocan al eje x, las soluciones de la ecuación son representadas con números complejos.
Los números complejos son particularmente útiles en la electricidad, sobre todo en la electrónica de corriente alterna (AC). La electricidad de corriente alterna produce una onda sinusoidal debido a que cambia entre positivo y negativo.
El cálculo de este tipo de corriente podría resultar demasiado complicado, ya que las ondas no encajan apropiadamente. Sin embargo, el cálculo de corrientes alternas se simplifica enormemente con el uso de los números complejos.
Otra aplicación de los números complejos es en el procesamiento de señales, lo cual es usado en la tecnología de celulares, en tecnologías inalámbricas, en radares e incluso en la neurología con las ondas cerebrales.
Básicamente, los números complejos son usados para facilitar el cálculo de procesos o aplicaciones que usan ondas seno o coseno.
¿Cuál es el origen de los números complejos?
Es difícil encontrar el origen exacto de los números complejos, ya que estos números estaban siendo usados por matemáticos mucho antes de tener una definición apropiada.
Se conoce que la primera referencia a los números complejos fue por Cardano en 1545 mientras estaba estudiando las raíces de los polinomios. Durante este periodo, se usó la notación del número $latex \sqrt{-1}$.
Sin embargo, esta notación solo fue usada con el fin de categorizar a las propiedades de algunos polinomios. En ese entonces, solo se consideraba a $latex \sqrt{-1}$ como una notación útil para categorizar polinomios y no era visto como un objeto matemático real.
La notación i fue introducida por Euler en 1777. Euler definió a i y –i como las dos raíces cuadradas de -1. Fue con Euler que apareció y se formalizó la notación “i” para números imaginarios. Sin embargo, debido a que la existencia de estos números no era entendida completamente, los números i y –i fueron llamados “imaginarios”.
En 1797 y 1799, Wessel y Gauss respectivamente, le dieron una interpretación geométrica a los números complejos al representarlos como puntos en un plano. Con esto se logró que los números complejos sean considerados como algo más concreto y menos misterioso.
Fue en 1833 que Hamilton finalmente definió formalmente a los números complejos al mostrar que estos números son compuestos de pares de números reales y de los números a los que Euler definió como “i“. Aquí fue en donde empezó la formulación moderna de los números complejos.
Véase también
¿Interesado en aprender más sobre números imaginarios y complejos? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
