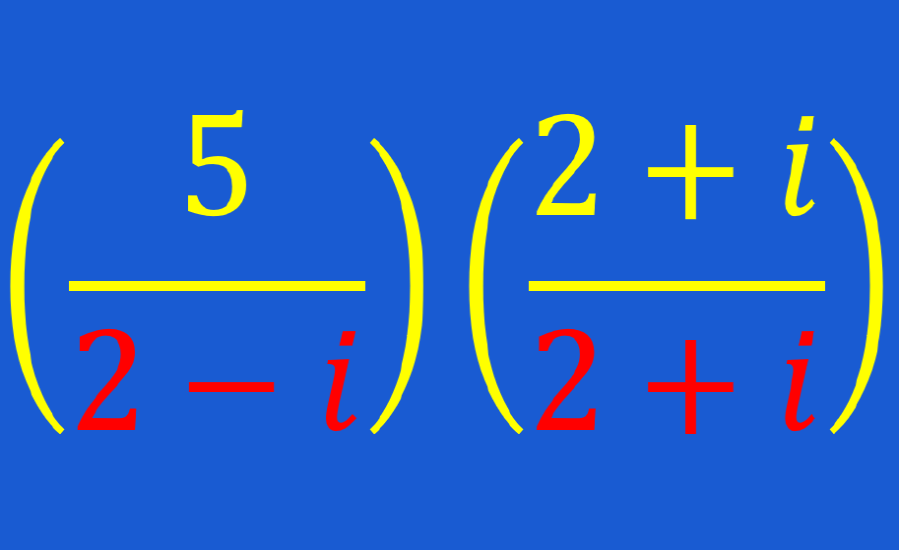Podemos resolver ejercicios con números complejos, tenemos que empezar analizando la operación a realizarse. Si es que tenemos sumas y restas, simplemente tenemos que sumar o restar las partes real e imaginaria separadamente. Si es que tenemos multiplicaciones, usamos la propiedad distributiva para multiplicar cada parte de un número complejo por cada parte del otro número. En el caso de división, tenemos que multiplicar tanto al numerador como al denominador por el conjugado de número complejo en el denominador.
A continuación, exploraremos estas operaciones con varios ejercicios.
¿Cómo resolver operaciones con números complejos?
Para resolver operaciones con números complejos, debemos recordar que las partes real e imaginaria son consideradas separadamente y que, cuando tenemos i², esto es igual a -1. Las operaciones básicas que podemos realizar con números complejos son la suma, resta, multiplicación y división.
Suma y resta de números complejos
Para sumar y restar números complejos, tenemos que sumar o restar las partes real e imaginaria separadamente. Por ejemplo, si tenemos los números $latex z_{1}=4+2i$ y $latex z_{2}=3+5i$, calculamos la suma de estos números de la siguiente manera:
$latex z_{1}+z_{2}=(4+3)+(2+5)i$
$latex =7+7i$
De igual forma, si es que queremos restar a estos números, calculados de la siguiente forma:
$latex z_{1}-z_{2}=(4-3)+(2-5)i$
$latex =1-3i$
Multiplicación de números complejos
Para obtener el producto de dos o más números complejos, tenemos que usar la propiedad distributiva y multiplicar cada una de las partes del primer número por cada una de las partes del segundo número.
Además, debemos recordar que cuando tenemos i², esto es igual a -1. Por ejemplo, multiplicamos a los números $latex z_{1}=2+6i$ y $latex z_{2}=3+5i$ de la siguiente manera:
$latex z_{1}z_{2}=(2+6i)(3+5i)$
$$=(2)(3)+(2)(5i)+(6i)(3)+(6i)(5i)$$
$latex =6+10i+18i+30{{i}^2}$
$latex =6+28i+30(-1)$
$latex =6+28i-30$
$latex =-24+28i$
División de números complejos
Para resolver una división de números complejos, tenemos que multiplicar tanto al numerador como al denominador por el conjugado del denominador.
Recordemos que el conjugado de un número complejo es obtenido al cambiar al signo del medio del número complejo original. Podemos resolver la división $latex \frac{4+5i}{2-3i}$ de la siguiente manera:
$$\frac{4+5i}{2-3i}=\frac{4+5i}{2-3i}\times \frac{2+3i}{2+3i}$$
$$=\frac{8+12i+10i+15{{i}^2}}{4-6i+6i-9{{i}^2}}$$
$$=\frac{8+22i-15}{4+9}$$
$$=\frac{-7+22i}{13}$$
$$=-\frac{7}{13}+\frac{22}{13}i$$
→ Cursos Gratis: Explora Nuestros Cursos de Matemáticas
Ejercicios con números complejos resueltos
Los siguientes ejercicios contienen varias operaciones básicas con números complejos como las mencionadas arriba. Cada ejercicio tiene su respectiva solución que puede ser usada para entender el razonamiento y el proceso usado para encontrar la respuesta.
EJERCICIO 1
Suma los números $latex z_{1}=5+8i$ y $latex z_{2}=2+9i$.
Solución
Para sumar números complejos, sumamos sus partes real e imaginaria separadamente. El número complejo resultante tiene la forma $latex z=a+bi$. Entonces, tenemos:
$latex a=5+2=7$
$latex b=8+9=17$
⇒ $latex z=7+17i$
EJERCICIO 2
Si tenemos los números $latex z_{1}=a+4i$, $latex z_{2}=7+bi$ y $latex z_{3}=5+7i$, ¿cuál es el valor de a y b si es que $latex z_{3}=z_{1}+z_{2}$
Solución
La parte real del número resultante es la suma de las partes reales de los números $latex z_{1}$ y $latex z_{2}$ y la parte imaginaria es la suma de las partes imaginarias de los números $latex z_{1}$ y $latex z_{2}$. Entonces, tenemos:
$latex 5=a+7$
⇒ $latex a=-2$
$latex 7=4+b$
⇒ $latex b=3$
EJERCICIO 3
Resuelve la resta $latex z_{1}-z_{2}$ si es que tenemos $latex z_{1}=6-12i$ y $latex z_{2}=4+3i$.
Solución
Para restar números complejos, restamos sus partes real e imaginaria separadamente. El número complejo resultante tiene la forma $latex z=a+bi$. Entonces, tenemos:
$latex a=6-4=2$
$latex b=-12-3=-15$
⇒ $latex z=2-15i$
EJERCICIO 4
Si tenemos los números $latex z_{1}=a+6i$, $latex z_{2}=-6+bi$ y $latex z_{3}=8-4i$, ¿cuál es el valor de a y b si es que $latex z_{3}=z_{1}-z_{2}$.
Solución
Podemos restar a las partes reales e imaginarias de los números $latex z_{1}$ y $latex z_{2}$ separadamente. Entonces, tenemos:
$latex 8=a-(-6)$
⇒ $latex a=2$
$latex -4=6-b$
⇒ $latex b=10$
EJERCICIO 5
Resuelve la multiplicación de los números complejos $latex (3+2i)(4+3i)$.
Solución
Para resolver esta multiplicación, tenemos que multiplicar cada uno de los términos del paréntesis de la izquierda por cada uno de los términos del paréntesis de la derecha. Entonces, tenemos:
$latex (3+2i)(4+3i)$
$$=(3)(4)+(3)(3i)+(2i)(4)+(2i)(3i)$$
$latex =12+9i+8i+6{{i}^2}$
$latex =12+17i+6{{i}^2}$
Recordamos que $latex {{i}^2}=-1$, por lo que tenemos:
$latex =12+17i+6(-1)$
$latex =12+17i-6$
$latex =6+17i$
EJERCICIO 6
¿Cuál es el producto de $latex z_{1}=(5-3i)$ y $latex z_{2}=(-2+4i)$.
Solución
Formamos y expandimos la multiplicación de los números complejos:
$latex z_{1}z_{2}=(5-3i)(-2+4i)$
$$=(5)(-2)+(5)(4i)+(-3i)(-2)+(-3i)(4i)$$
$latex =-10+20i+6i-12{{i}^2}$
$latex =-10+26i-12{{i}^2}$
Nuevamente, usamos el hecho que $latex {{i}^2}=-1$:
$latex =-10+26i+12$
$latex =2+26i$
EJERCICIO 7
Resuelve la división $latex \frac{5+2i}{3-5i}$.
Solución
Para resolver una división de números complejos, tenemos que multiplicar tanto al numerador como al denominador por el conjugado del denominador. En este caso, el conjugado del denominador es $latex 3+5i$. Entonces, tenemos:
$latex \frac{5+2i}{3-5i}=\frac{5+2i}{3-5i}\times \frac{3+5i}{3+5i}$
$latex =\frac{15+25i+6i+10{{i}^2}}{9+15i-15i-25{{i}^2}}$
$latex =\frac{15+31i-10}{9+25}$
$latex =\frac{5+31i}{34}$
Ya obtuvimos la respuesta, pero tenemos que escribir a la parte real e imaginaria separadamente:
$latex =\frac{5}{34}+\frac{31}{34}i$
EJERCICIO 8
Resuelve la división $latex \frac{4+2i}{2+3i}$.
Solución
En este caso, el conjugado del denominador es $latex 2-3i$, por lo que multiplicamos tanto al numerador como al denominador por ese número:
$latex \frac{4+2i}{2+3i}=\frac{4+2i}{2+3i}\times \frac{2-3i}{2-3i}$
$latex =\frac{8-12i+4i-6{{i}^2}}{4-6i+6i-9{{i}^2}}$
$latex =\frac{8-8i+6}{4+9}$
$latex =\frac{14-8i}{13}$
Ya obtuvimos la respuesta, pero tenemos que escribir a la parte real e imaginaria separadamente:
$latex =\frac{14}{13}-\frac{8}{13}i$
Únete a nuestros cursos interactivos o practica con nuestros generadores de problemas
Ejercicios con números complejos para resolver
Practica lo aprendido sobre las operaciones con números complejos al resolver los siguientes ejercicios. Si necesitas ayuda con estos ejercicios, puedes mirar los ejercicios resueltos de arriba.
→ Explora más ejercicios de práctica
Véase también
¿Interesado en aprender más sobre números complejos? Mira estas páginas:
