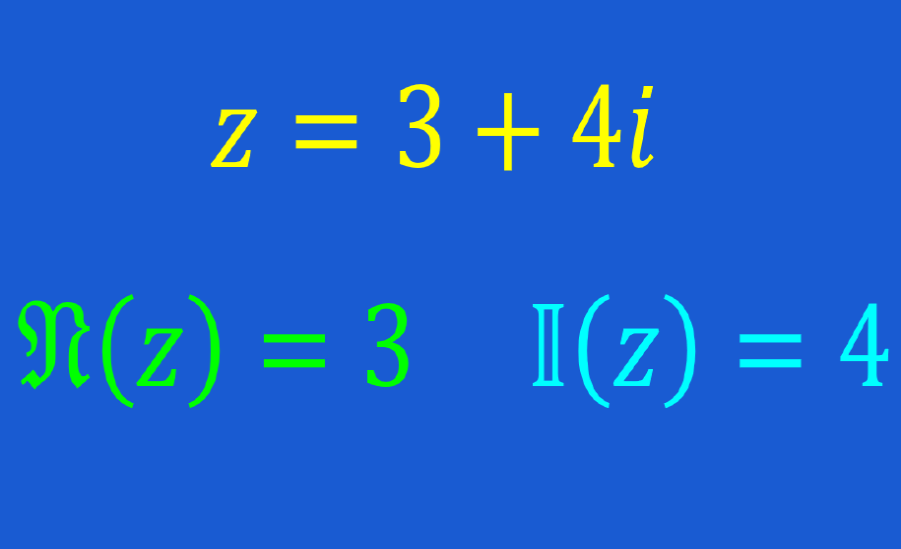Los números complejos tienen varias propiedades matemáticas muy útiles que facilitan enormemente el modelaje de sistemas sinusoidales como por ejemplo circuitos eléctricos.
Básicamente, trabajamos con números complejos para evitar algunas calculaciones y simplificar los problemas matemáticos.
¿Qué son los números complejos?
Los números complejos son números que toman la forma de un número real más un número imaginario. Recordemos que los números reales son números como $latex 3, -4.5, \frac{3}{5}, \sqrt{3}$.
Los números imaginarios son aquellos números que al ser elevados al cuadrado son igual a un número negativo. La unidad imaginaria es i, lo cual es igual a la raíz cuadrada de -1: $latex i=\sqrt{-1}$.
EJEMPLOS
Los siguientes son ejemplos de números complejos:
- $latex 3+i$
- $latex 2+3i$
- $latex 10-5i$
- $latex -4-4i$
Aplicaciones de los números imaginarios
Para la mayoría de nuestras tareas en la vida cotidiana, los números reales ofrecen una descripción adecuada de los datos. Fracciones tales como $latex \frac{1}{3}$ o $latex \frac{5}{3}$ no tienen sentido si es que estamos contando personas, pero son esenciales si es que estamos cuantificando partes de un grupo de personas.
Los números negativos como $latex -2$ o $latex -13$ no tienen sentido cuando estamos midiendo la longitud de un objeto, pero son esenciales cuando estamos hablando de deudas o créditos.
De igual forma, los números imaginarios no son útiles para el conteo de objetos de la vida cotidiana, pero son esenciales en aplicaciones concretas en varias áreas de ingeniería y ciencia como el proceso de señales, la teoría del control, electromagnetismo, análisis de vibraciones, mecánica cuántica y otras.
Aplicaciones de los números complejos en la ingeniería
Las siguientes son algunas de las aplicaciones de los números complejos en la ingeniería:
Teoría del Control: En la teoría del control, los sistemas son transformados del dominio del tiempo al dominio de la frecuencia usando transformaciones de Laplace. Los polos y los ceros del sistema son analizados en el plano complejo.
Análisis de Señales: Los números complejos son usados en el análisis de señales y otros campos para obtener una descripción conveniente de señales que varían periódicamente. Para dadas funciones reales que representan cantidades físicas, muchas veces en términos de seno y coseno, podemos considerar funciones complejas correspondientes de las cuales, las partes reales son las cantidades originales.
Para una onda seno de una dada frecuencia, el valor absoluto |z| del número correspondiente z es la amplitud y el argumento arg(z) es la fase.
Integrales Impropias: Para campos aplicados como la ingeniería, los números complejos son usados frecuentemente para calcular integrales impropias con valores de la vida real al usar funciones de números complejos.
En Ingeniería Mecánica y Civil: El concepto de geometría compleja y el plano complejo es muy útil en la construcción de edificios y autos. Este concepto es usado en el diseño 2D de edificios y autos. Los números complejos también pueden ser usados en mecánica para representar rotaciones.
Teorema de los Residuos: El teorema de los residuos en análisis complejo es una poderosa herramienta para evaluar integrales de caminos de funciones meromórficas con respecto a curvas cerradas y muchas veces también puede ser usada para calcular integrales reales.
Aplicaciones de los números complejos en la informática
Los números complejos no son particularmente fundamentales en la informática, pero aparecen en varios lugares en donde su conocimiento es necesario para construir aplicaciones. El primer lugar en donde vemos a los números complejos en la informática es en el ejemplo prototípico de una clase o un tipo.
Un número complejo es un ejemplo fácil de entender de un objeto en el sentido de la programación orientada a objetos. Podemos mostrar los datos, una parte real y una parte imaginaria y las operaciones en los datos implementadas como métodos. Este es un raro caso del uso de la sobrecarga del operador.
El segundo lugar es en gráficas computacionales. En el caso 2D, los puntos pueden ser números complejos y las rotaciones, traslaciones y reflexiones de esos puntos corresponden a varias operaciones en los números complejos. Los números complejos se generalizan a cuaterniones, los cuales son útiles para gráficas 3D.
Hay otros lugares en donde los números complejos pueden aparecer, generalmente como conocimiento de la aplicación que necesita ser entendida antes de que un programa pueda ser escrito. Por ejemplo, necesitaríamos números complejos para sistemas computacionales algebraicos o simulaciones de mecánica cuántica.
Aplicaciones de los números complejos en la electrónica
Los números complejos tienen aplicaciones fundamentales en la electrónica. El voltaje producido por una batería es caracterizado por un número real llamado potencial, por ejemplo, +10 voltios o -10 voltios. Sin embargo, el voltaje “AC” en una casa requiere dos parámetros. El uno es un potencial, como 120 voltios y el otro es un ángulo llamado la fase.
El voltaje tiene dos dimensiones y una cantidad bidimensional puede ser representada matemáticamente como un vector o un número complejo (conocido en ingeniería como un fasor).
En la representación de vectores, las coordenadas rectangulares son referidas simplemente como X y Y. En la representación de números complejos, los mismos componentes son referidos como real y como imaginario. Cuando el número complejo es puramente imaginario, como por ejemplo, una parte real de 0 y una parte imaginaria de 120, eso significa que el voltaje tiene un potencial de 120 voltios y una fase de 90°, lo cual es una medida completamente real.
En la ingeniería eléctrica, la transformación de Fourier es usada para analizar voltajes y corrientes variantes. El trato de resistores, capacitores e inductores puede ser unificado al introducir resistencias imaginarias que son dependientes de la frecuencia y combinarlos en un solo número complejo llamado la impedancia.
Este uso también es extendido a procesamiento de señales digitales y a procesamiento de imágenes digitales, los cuales utilizan versiones digitales de análisis de Fourier para trasmitir, comprimir y restaurar las señales de imágenes, auto o video. Los ingenieros eléctricos usan la letra j para la unidad imaginaria, ya que es típicamente reservada para corrientes variantes.
Aplicaciones de los números complejos en la física
Las siguientes son las áreas de la física en las que los números complejos son usados:
Mecánica de Fluidos: La mecánica de fluidos y sus subdisciplinas como aerodinámica, hidrodinámica e hidráulica tienen una gran variedad de aplicaciones. Por ejemplo, podemos calcular las fuerzas y los momentos de inercia en un avión, el flujo de masa del petróleo a través de los oleoductos y las predicciones de patrones del clima. En mecánica de fluidos, los números complejos son usados para describir el flujo potencial en dos dimensiones.
Electromagnetismo: En vez de tomar a las partes magnética y eléctrica como dos números reales diferentes, podemos representarlo como un número complejo.
Relatividad: En relatividad general y especial, algunas fórmulas para medir el tiempo espacio se vuelven más simples si es que tomamos a la variable del tiempo como imaginaria. A pesar de que esto ya no es estándar en relatividad clásica, es usada en una manera esencial en la teoría de campos cuánticos.
Mecánica cuántica: Los números complejos son relevantes en la formulación de la mecánica cuántica, en donde espacios Hilbert complejos proveen el espacio para tales formulaciones que son convenientes y tal vez estándar. Las fórmulas fundacionales de mecánica cuántica – la ecuación de Schrödinger y la mecánica de matrices de Heisenberg – usan los números complejos.
Véase también
¿Interesado en aprender más sobre otros temas algebraicos? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
