El teorema de ángulos inscritos indica que, cuando tenemos a un ángulo central y a un ángulo inscrito que intersecan en el mismo arco del círculo, el ángulo central es el doble del ángulo inscrito. Dependiendo en cómo se ubiquen los ángulos, podemos tener tres casos diferentes de este teorema. Cada uno de estos casos necesita un método diferente para ser demostrado.
A continuación, conoceremos las diferentes pruebas que podemos usar para demostrar el teorema de ángulos inscritos.
GEOMETRÍA
Relevante para…
Aprender sobre las tres pruebas del teorema de ángulos inscritos.
GEOMETRÍA
Relevante para…
Aprender sobre las tres pruebas del teorema de ángulos inscritos.
Explicación del teorema de ángulos inscritos
El teorema de ángulos inscritos indica que, cuando el ángulo central y el ángulo inscrito comparten puntos finales en el círculo, el valor del ángulo central es el doble que el ángulo inscrito.
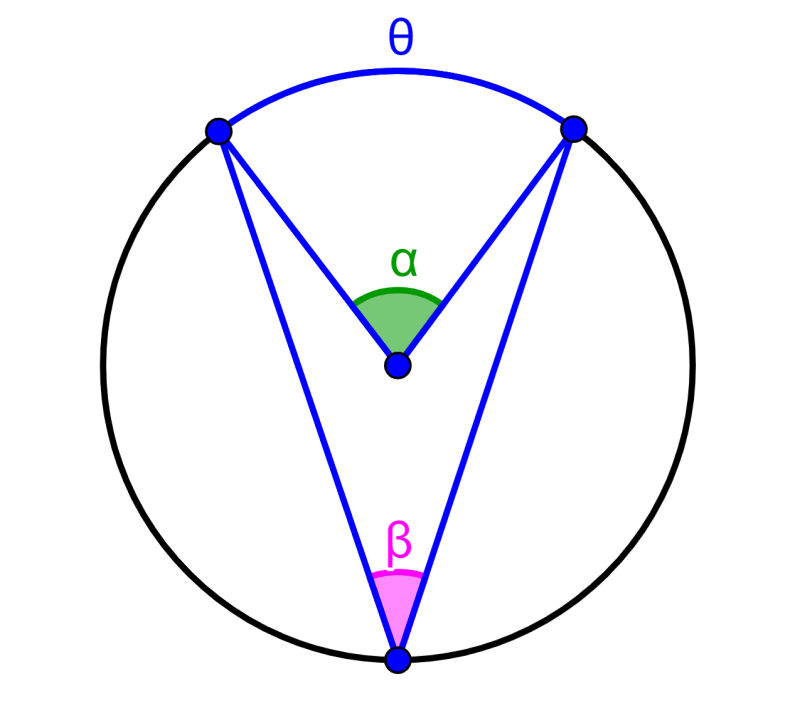
Recordemos que un ángulo inscrito es un ángulo en el interior del círculo que se forma en donde dos cuerdas se encuentran.
Un ángulo central es un ángulo en el interior de un círculo, en el cual el vértice es el centro del círculo y los lados son los radios.
En el siguiente diagrama, el ángulo verde es un ángulo central y el ángulo rosa es un ángulo inscrito.
Prueba del caso 1: Ángulo inscrito entre una cuerda y el diámetro del círculo
Este caso puede ser observado en el siguiente diagrama:
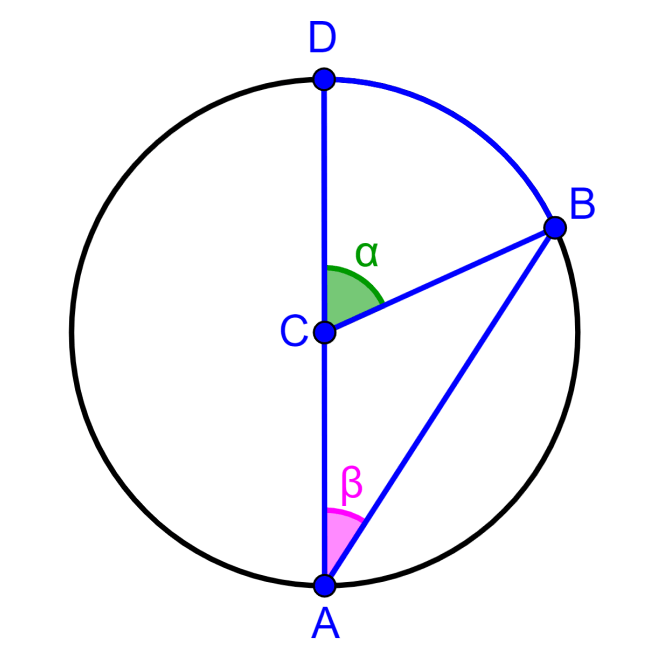
Vamos a probar que α=2β.
En este diagrama, el triángulo ABC es un triángulo isósceles, ya que los segmentos AC y BC son radios del círculo y tenemos AC=BC. Entonces, los ángulos ∠CAB y ∠ABC son iguales. Es decir, tenemos ∠CAB=∠ABC=β.
El diámetro AD es una línea recta, por lo que el ángulo ∠BCA=(180-α)°.
Sabemos que los ángulos en un triángulo suman 180°, por lo que tenemos:
∠CAB+∠ABC+∠BCA=180°
Ahora, simplificamos los ángulos con sus valores conocidos y tenemos:
β+β+180°-α=180°
Simplificando y resolviendo, tenemos:
β+β+180°-α=180°
2β-α=0
2β=α
Hemos demostrado el teorema.
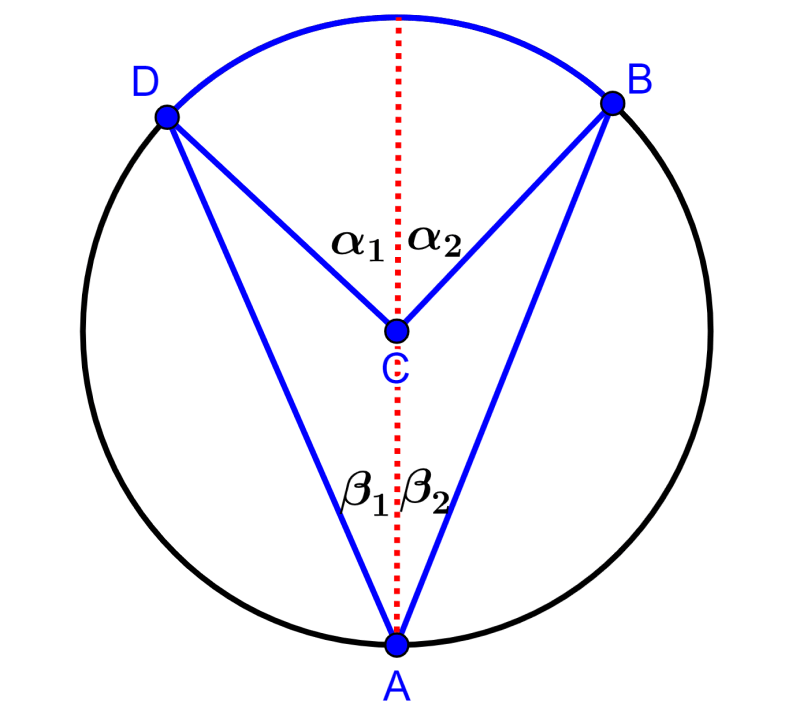
Prueba del caso 2: Diámetro entre los lados del ángulo inscrito
En el siguiente diagrama, podemos mirar el segundo caso:
Vamos a probar que 2β=α.
Podemos trazar el diámetro del círculo y representar a los ángulos importantes.
Podemos ver que el diámetro divide a los ángulos α y β. Entonces, tenemos:
$latex \alpha_{1}+\alpha_{2}=\alpha$
$latex \beta_{1}+\beta_{2}=\beta$
Tomando en cuenta el primer caso que vimos arriba, podemos deducir lo siguiente:
$latex 2\beta_{1}=\alpha_{1}$
$latex 2\beta_{2}=\alpha_{2}$
Ahora, podemos sumar los ángulos y simplificar usando $latex \alpha=\alpha_{1}+\alpha_{2}$ y $latex \beta=\beta_{1}+\beta_{2}$:
$latex 2\beta_{1}+2\beta_{2}=\alpha_{1}+\alpha_{2}$
$latex 2\beta=\alpha$
Hemos demostrado el teorema.
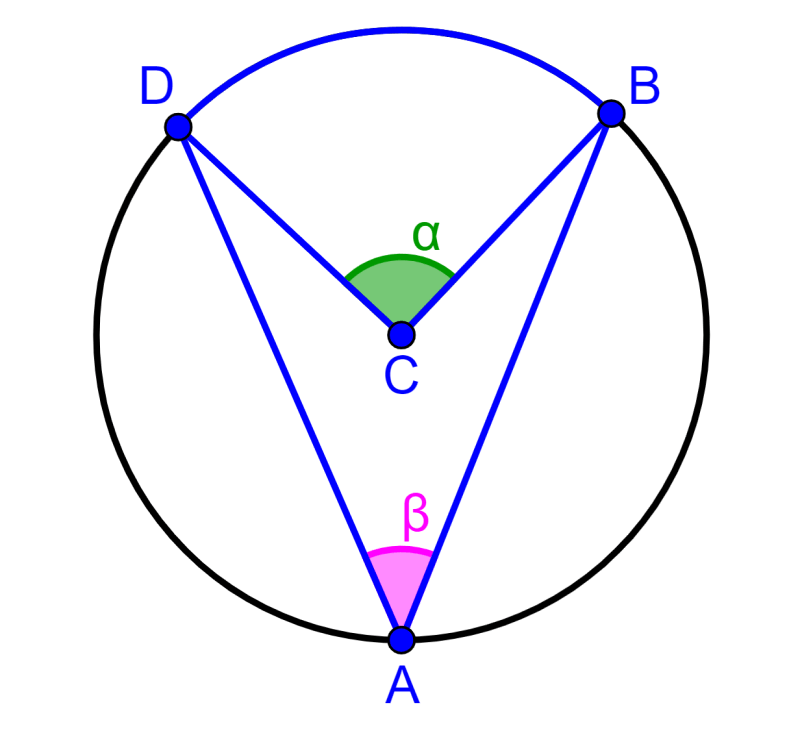
Prueba del caso 3: Diámetro fuera de los lados del ángulo inscrito
Este caso es representado en el siguiente diagrama:
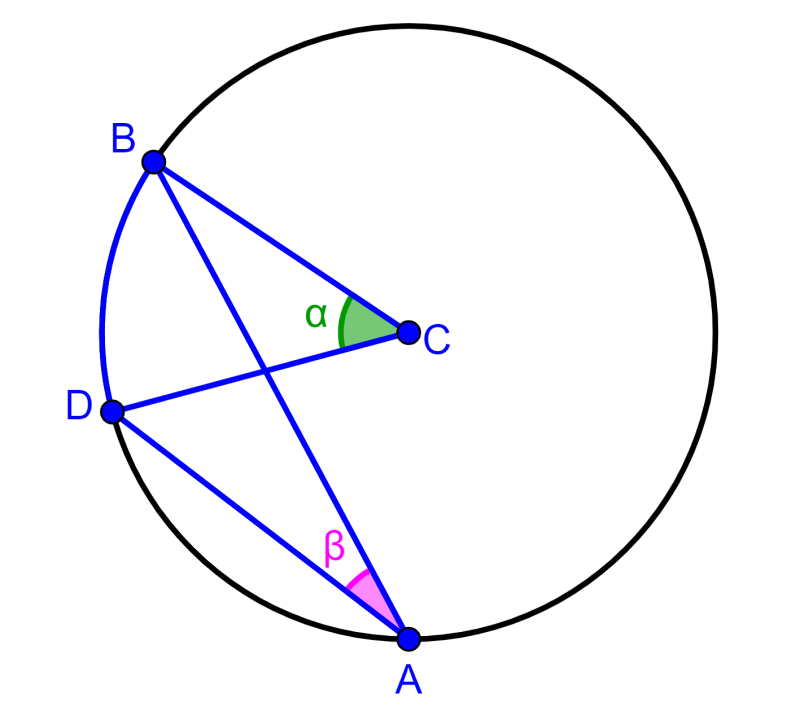
Vamos a probar que 2β=α.
Similar al caso anterior, vamos a trazar el diámetro del círculo y a representar a los ángulos importantes.
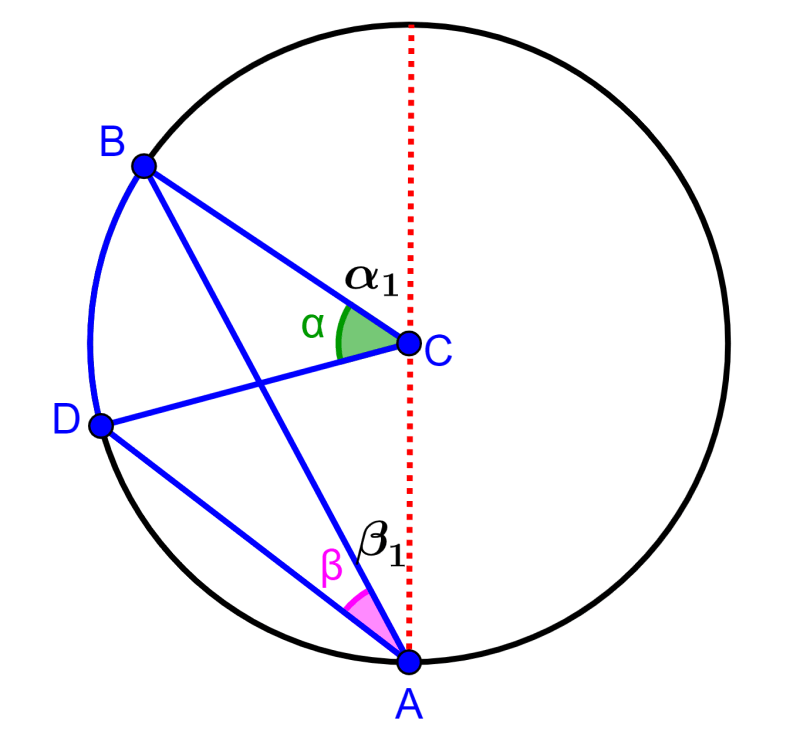
Nuevamente, sabemos que $latex 2\beta_{1}=\alpha_{1}$. Entonces, tenemos:
$latex 2(\beta_{1}+\beta)=\alpha+\alpha_{1}$
Sustituyendo $latex 2\beta_{1}=\alpha_{1}$, tenemos:
$latex 2(\beta_{1}+\beta)=\alpha+2\beta_{1}$
$latex 2\beta_{1}+2\beta=\alpha+2\beta_{1}$
$latex 2\beta=\alpha$
Hemos demostrado el teorema.
Véase también
¿Interesado en aprender más sobre ángulos inscritos y otros tipos de ángulos? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
