Un paralelo es una figura bidimensional que tiene lados que son paralelos los unos con los otros. El paralelogramo es un tipo de polígono que tiene cuatro lados (llamado cuadrilátero), en donde el par de lados paralelos son iguales en longitud. Además, los ángulos internos opuestos de un paralelogramo tienen las mismas medidas. La suma de los ángulos adyacentes de un paralelogramo es igual a 180 grados.
A continuación, conoceremos las propiedades fundamentales de los paralelogramos. También, veremos las fórmulas de los paralelogramos más importantes y las usaremos para resolver algunos problemas.
GEOMETRÍA
Relevante para…
Aprender las propiedades fundamentales de los paralelogramos.
GEOMETRÍA
Relevante para…
Aprender las propiedades fundamentales de los paralelogramos.
Definición del paralelogramo
Un paralelogramo es un cuadrilátero con dos pares de lados paralelos. Los lados opuestos del paralelogramo tienen la misma longitud y los ángulos opuestos tienen la misma medida.
Además, los ángulos internos en el mismo lado del transversal son suplementarios. La suma de todos los ángulos internos es igual a 360 grados.
Un cuadrado y un rectángulo son dos figuras que tienen propiedades similares a un paralelogramo.
Si es que los lados de un paralelogramo son congruentes o iguales el uno con el otro, entonces, la figura es un rombo.
La siguiente es la imagen de un paralelogramo:
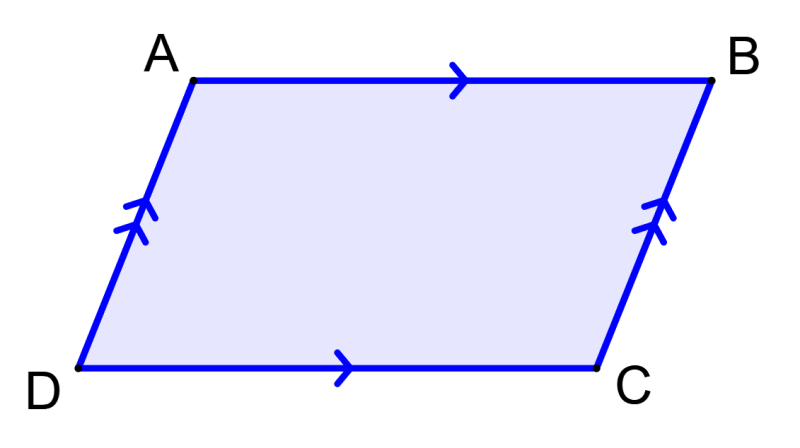
En la figura, podemos ver que AB y CD son paralelos, así como también los lados AD y BC. Además, los lados AB y CD son iguales y los lados AD y BC también son iguales.
El ángulo A es igual al ángulo C y el ángulo B es igual al ángulo D. Además, los ángulos A y D son suplementarios, ya que estos ángulos se ubican en el mismo lado del transversal. De igual forma, los ángulos B y C son suplementarios. Entonces, estos ángulos suman 180°.
Propiedades fundamentales de los paralelogramos
Las propiedades fundamentales de los paralelogramos son las siguientes:
- Los lados opuestos son paralelos.
- Los lados opuestos son congruentes (tienen la misma longitud).
- Los ángulos consecutivos son suplementarios.
- Si es que uno de los ángulos es un ángulo recto, entonces los otros ángulos también serán ángulos rectos.
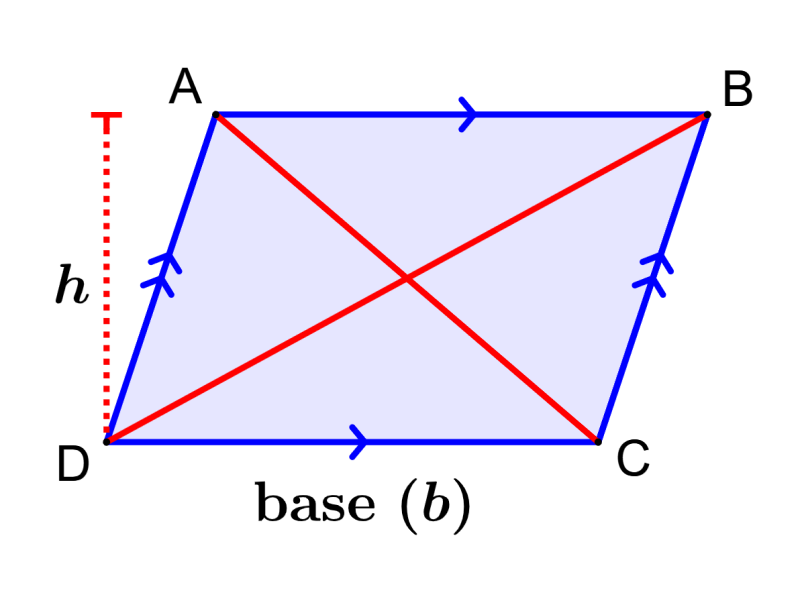
- Las dos diagonales bisecan la una a la otra.
- Cada diagonal biseca al paralelogramo en dos triángulos congruentes.
- La suma del cuadrado de las longitudes de todos los lados del paralelogramo es igual a la suma del cuadrado de sus diagonales.
Fórmulas de los paralelogramos
Las fórmulas para el área y el perímetro de un paralelogramo pueden ser usadas para resolver problemas.
Área del paralelogramo
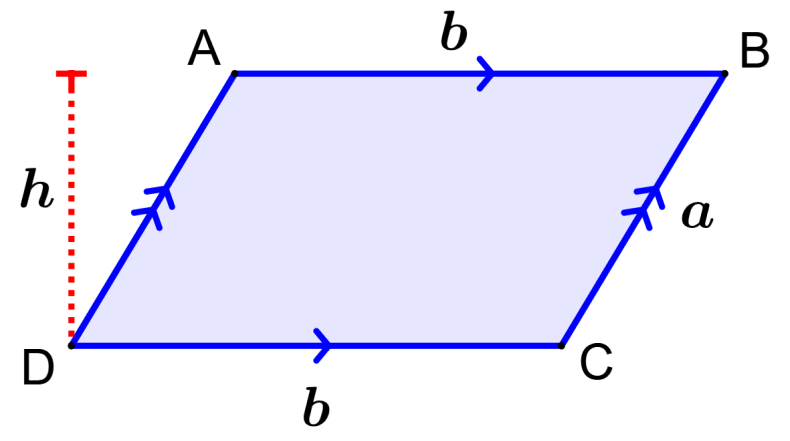
El área del paralelogramo es la región ocupada por la figura en el plano bidimensional. La siguiente es la fórmula para encontrar el área del paralelogramo:
| Área = Base × Altura $latex A=b\times h$ |
Perímetro del paralelogramo
El perímetro de cualquier figura es la distancia total cubierta alrededor de la figura. De igual forma, el perímetro del paralelogramo es la distancia total de los límites del paralelogramo.
Para calcular el perímetro, necesitamos conocer las longitudes de sus lados. Un paralelogramo tiene sus lados opuestos iguales en longitud. Entonces, la fórmula del perímetro es:
| $latex p=2(a+b)$ |
en donde, a y b son las longitudes de los lados del paralelogramo.
Ejemplos de problemas de paralelogramos
EJEMPLO 1
- ¿Cuál es el área de un paralelogramo que tiene lados de longitud 13 m y 15 m?
Solución: Tenemos los siguientes datos:
- Base, $latex b=13$ m
- Altura, $latex h=15$ m
Entonces usamos la fórmula del área con estos valores:
$latex A=bh$
$latex A=(13)(15)$
$latex A=195$
El área del paralelogramo es 195 m².
EJEMPLO 2
- ¿Cuál es el perímetro de un paralelogramo que tiene lados de longitud 21 cm y 22 cm?
Solución: Tenemos los siguientes valores:
- Lado 1, $latex a=21$ m
- Lado 2, $latex b=22$ m
Entonces usamos la fórmula del perímetro con estos valores:
$latex p=2(a+b)$
$latex p=2(21+22)$
$latex p=2(43)$
$latex p=86$
El perímetro del paralelogramo es 86 m.
Véase también
¿Interesado en aprender más sobre paralelogramos? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
