Un paralelogramo es un cuadrilátero en el cual, los lados opuestos son paralelos y tienen la misma longitud. Al tener lados opuestos que son paralelos y con iguales longitudes, hace que los ángulos en los lados opuestos también sean iguales. Las diagonales de un paralelogramo son los segmentos que conectan las esquinas opuestas de la figura.
A continuación, conoceremos las fórmulas que podemos usar para calcular las diagonales de un paralelogramo. Además, veremos algunos ejercicios resueltos en los que aplicaremos estas fórmulas.
GEOMETRÍA
Relevante para…
Aprender sobre la diagonal de un paralelogramo con ejercicios.
GEOMETRÍA
Relevante para…
Aprender sobre la diagonal de un paralelogramo con ejercicios.
Fórmula de la diagonal del paralelogramo
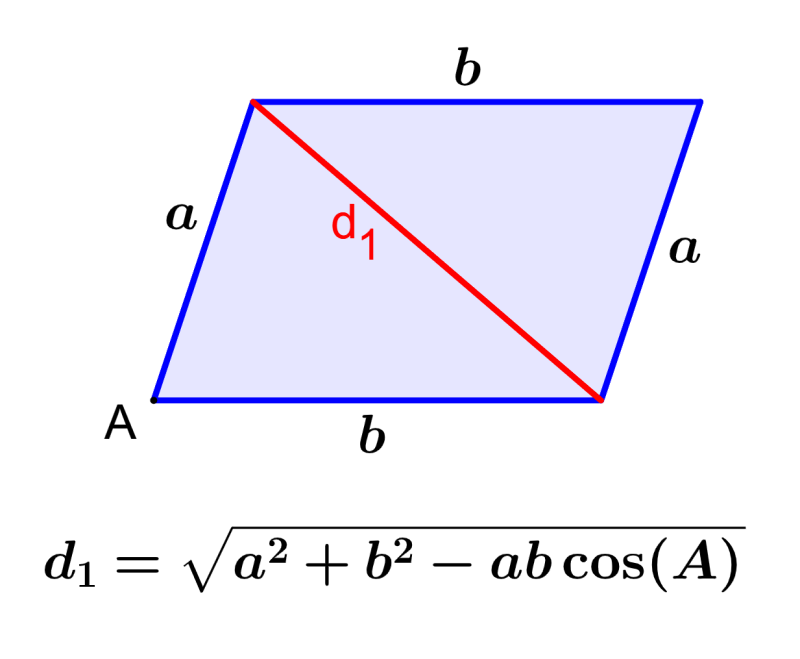
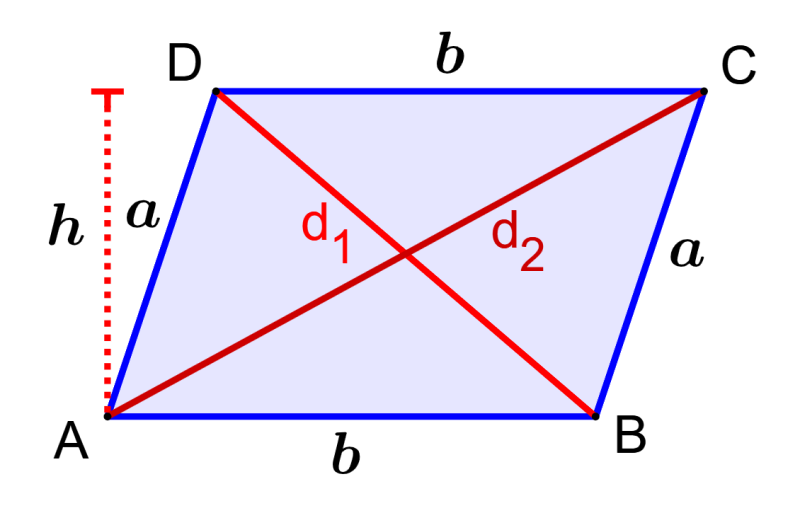
Consideremos al siguiente paralelogramo:
Para encontrar las diagonales de este paralelogramo, podemos usar las siguientes fórmulas:
$latex d_{1}=\sqrt{{{a}^2}+{{b}^2}-2ab\cos(A)}$
$latex d_{1}=\sqrt{{{a}^2}+{{b}^2}+2ab\cos(B)}$
$latex d_{2}=\sqrt{{{a}^2}+{{b}^2}+2ab\cos(A)}$
$latex d_{2}=\sqrt{{{a}^2}+{{b}^2}-2ab\cos(B)}$
$latex {{d_{1}}^2}+{{d_{2}}^2}=2({{a}^2}+{{b}^2})$
en donde,
- $latex d_{1}, ~d_{2}$ son las longitudes de las diagonales
- $latex a, ~b$ son las longitudes de los lados
Ejercicios de diagonal de un paralelogramo resueltos
En los siguientes ejercicios, usamos las fórmulas de las diagonales para calcular las longitudes de las diagonales de los paralelogramos. Intenta resolver los ejercicios tú mismo antes de mirar la respuesta.
EJERCICIO 1
Encuentra la diagonal de un paralelogramo con lados 6 m y 10 m y ángulo de 30°.
Solución
Tenemos los siguientes datos:
- Lado 1, $latex a=6$ m
- Lado 2, $latex b=10$ m
- Ángulo, $latex A=30°$
Entonces, usamos la fórmula de la diagonal con estos valores:
$latex d_{1}=\sqrt{{{a}^2}+{{b}^2}-2ab\cos(A)}$
$latex d_{1}=\sqrt{{{6}^2}+{{10}^2}-2(6)(10)\cos(30°)}$
$latex d_{1}=\sqrt{36+100-2(6)(10)(0.5)}$
$latex d_{1}=\sqrt{136-60}$
$latex d_{1}=\sqrt{76}$
$latex d_{1}=8.72$
La diagonal tiene una longitud de 8.72 m.
EJERCICIO 2
¿Cuál es la diagonal de un paralelogramo con lados de longitud 10 m y 13 m y un ángulo que mide 40°?
Solución
Podemos identificar los siguientes:
- Lado 1, $latex a=10$ m
- Lado 2, $latex b=13$ m
- Ángulo, $latex A=40°$
Entonces, reemplazamos estos valores en la fórmula:
$latex d_{1}=\sqrt{{{a}^2}+{{b}^2}-2ab\cos(A)}$
$$d_{1}=\sqrt{{{10}^2}+{{13}^2}-2(10)(13)\cos(40°)}$$
$latex d_{1}=\sqrt{100+169-2(10)(13)(0.643)}$
$latex d_{1}=\sqrt{269-167.18}$
$latex d_{1}=\sqrt{101.82}$
$latex d_{1}=10.09$
La diagonal tiene una longitud de 10.09 m.
EJERCICIO 3
Un paralelogramo tiene lados de longitud 8 m y 14 m con un ángulo que mide 45°. ¿Cuál es la longitud de su diagonal?
Solución
Tenemos la siguiente información:
- Lado 1, $latex a=8$ m
- Lado 2, $latex b=14$ m
- Ángulo, $latex A=45°$
Al usar estos valores en la fórmula, tenemos:
$latex d_{1}=\sqrt{{{a}^2}+{{b}^2}-2ab\cos(A)}$
$latex d_{1}=\sqrt{{{8}^2}+{{14}^2}-2(8)(14)\cos(45°)}$
$latex d_{1}=\sqrt{64+196-2(8)(14)(0.707)}$
$latex d_{1}=\sqrt{260-158.368}$
$latex d_{1}=\sqrt{101.632}$
$latex d_{1}=10.08$
La diagonal tiene una longitud de 10.08 m.
EJERCICIO 4
¿Cuál es la longitud de la diagonal de un paralelogramo que tiene lados de longitud 5 m y 7 m y un ángulo que mide 40°?
Solución
Tenemos los siguientes datos:
- Lado 1, $latex a=5$ m
- Lado 2, $latex b=7$ m
- Ángulo, $latex A=40°$
Entonces, usamos la fórmula de la diagonal con estos valores:
$latex d_{1}=\sqrt{{{a}^2}+{{b}^2}-2ab\cos(A)}$
$latex d_{1}=\sqrt{{{5}^2}+{{7}^2}-2(5)(7)\cos(40°)}$
$latex d_{1}=\sqrt{25+49-2(5)(7)(0.643)}$
$latex d_{1}=\sqrt{74-45.01}$
$latex d_{1}=\sqrt{76}$
$latex d_{1}=5.38$
La diagonal tiene una longitud de 5.38 m.
Ejercicios de diagonal de un paralelogramo para resolver
Resuelve los siguientes ejercicios usando la fórmula de la diagonal de un paralelogramo. Selecciona tu respuesta y haz clic en “Verificar” para comprobar tu respuesta. Mira los ejercicios resueltos de arriba en caso de necesitar ayuda.
Véase también
¿Interesado en aprender más sobre paralelogramos? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
