Un cuadrado es una figura de dos dimensiones con cuatro lados iguales, en la que sus cuatro ángulos miden 90 grados. Las propiedades de los cuadrados son bastante similares a las de un rectángulo, pero la diferencia entre los dos es que, en un rectángulo solo sus lados opuestos son iguales. Las otras propiedades del cuadrado tales como área y perímetro, también difieren de las del rectángulo.
A continuación, veremos las propiedades fundamentales de los cuadrados. También, veremos algunos ejemplos de estas propiedades.
Propiedades fundamentales de los cuadrados
Las siguientes son las propiedades fundamentales de los cuadrados:
- Los cuatro ángulos internos de un cuadrado son iguales a 90°.
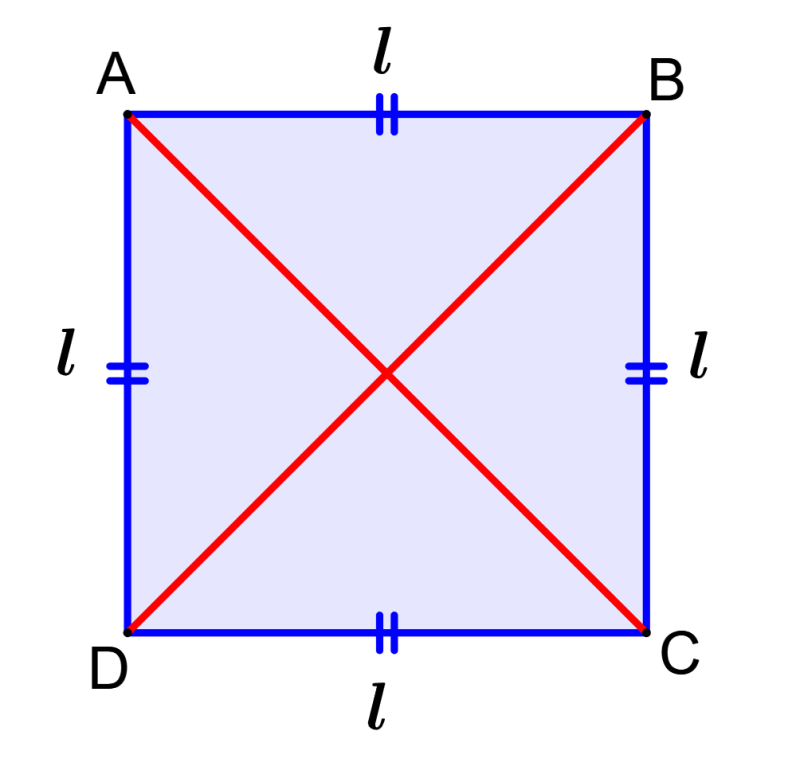
- Los cuatro lados de un cuadrado son congruentes (la longitud es la misma).
- Los lados opuestos del cuadrado son paralelos el uno con el otro.
- Las diagonales bisecan la una a la otra en 90°, es decir, son perpendiculares.
- Las dos diagonales son iguales (tienen la misma longitud).
- El cuadrado tiene cuatro vértices y cuatro lados.
- La diagonal de cuadrado lo divide en dos triángulos isósceles similares.
- La longitud de las diagonales es mayor que la longitud de los lados del cuadrado.
- Las diagonales del cuadrado son diámetros del circuncírculo del cuadrado.
- Un cuadrado es un equilátero con cuatro lados iguales y cuatro ángulos internos iguales.
- Un cuadrado es un rombo con cuatro ángulos iguales (cada ángulo tiene 90°).
- Un cuadrado es un rectángulo, en el que sus dos lados adyacentes son iguales.
- Un cuadrado es un paralelogramo con los cuatro ángulos internos iguales a 90° y los lados adyacentes iguales en longitud.
Fórmulas de los cuadrados
Las siguientes son algunas fórmulas importantes relacionadas con los cuadrados:
Área de un cuadrado: A=l², en donde l es la longitud de cada lado del cuadrado:
| Área del cuadrado = (lado)²=l² |
Perímetro de un cuadrado: p=longitud total de todos los lados del cuadrado = 4l, en donde l es la longitud de cada lado del cuadrado:
| Perímetro = 4 × lado=4l |
Diagonal de un cuadrado: Cada una de las diagonales, divide al cuadrado en dos triángulos rectángulos iguales, en donde la diagonal es la hipotenusa de los triángulos.
Podemos aplicar el teorema de Pitágoras para encontrar la longitud de la hipotenusa:
$latex {{d}^2}={{lado}^2}+{{lado}^2}$
Sabemos que un cuadrado tiene todos sus lados iguales, entonces, tenemos:
$latex {{d}^2}=2{{lado}^2}$
$latex d=\sqrt{2}~l$
Entonces,
| Diagonal =$latex \sqrt{2}~lado=\sqrt{2}~l$ |
Problemas de cuadrados
Los siguientes son algunos ejemplos de problemas de cuadrados resueltos.
EJEMPLO 1
- ¿Cuál es el perímetro de un cuadrado que tiene lados de longitud 13 m?
Solución: Sabemos que la fórmula del perímetro de un cuadrado es 4l, en donde l es la longitud de los lados del cuadrado. Entonces, usando $latex l=13$, tenemos:
$latex p=4l$
$latex p=4(13)$
$latex p=52$
El perímetro del cuadrado es 52 m.
EJEMPLO 2
- Si es que un cuadrado tiene lados de longitud 15 cm, ¿cuál es su área?
Solución: Un cuadrado tiene todos sus lados iguales y su área puede ser calculada al elevar a uno de sus lados al cuadrado. Entonces, usando la longitud dada, tenemos:
$latex A={{l}^2}$
$latex A={{15}^2}$
$latex A=225$
El área del cuadrado es 225 cm².
EJEMPLO 3
- ¿Cuál es la longitud de la diagonal de un cuadrado que tiene lados de longitud 8 m?
Solución: La diagonal del cuadrado es calculada usando el teorema de Pitágoras. Luego, de simplificar obtenemos la siguiente fórmula, en la que usamos $latex l=8$:
$latex d=\sqrt{2}~l$
$latex d=\sqrt{2}~(8)$
$latex d=8\sqrt{2}$
La diagonal del cuadrado tiene una longitud de $latex 8\sqrt{2}$ m.
Véase también
¿Interesado en aprender más sobre cuadrados? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
