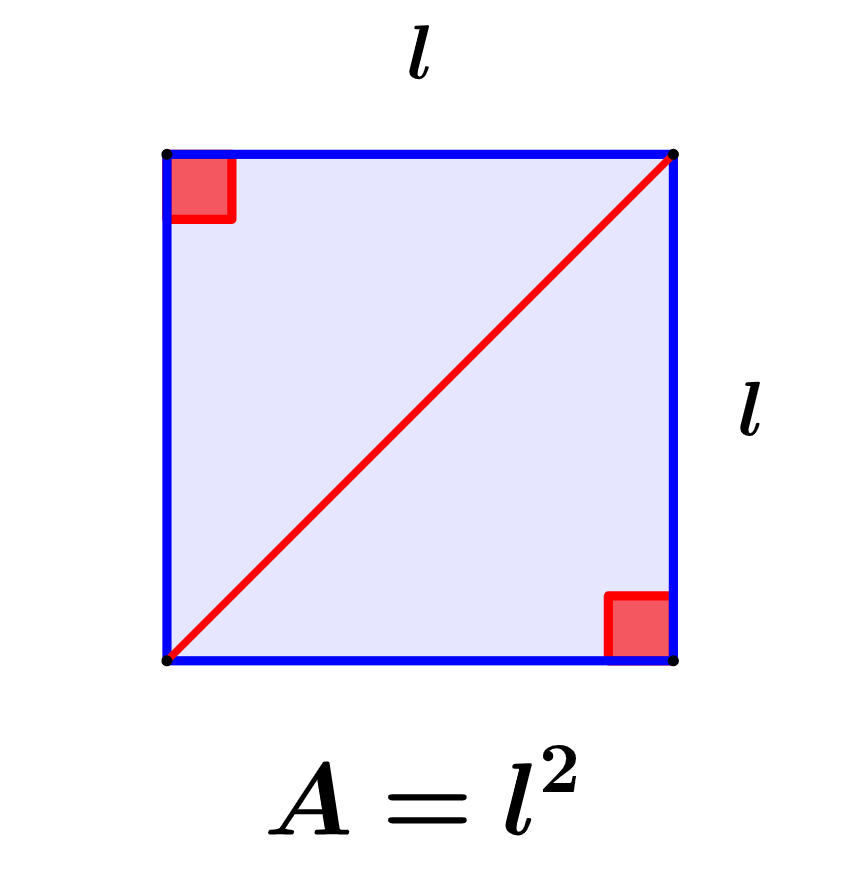
El área de un cuadrado es definida como el número de unidades cuadradas que se necesitan para llenar a un cuadrado. En general, el área es definida como la región ocupada dentro de los límites de una figura bidimensional. La medida es realizada en unidades cuadradas, en donde, la unidad estándar es metros cuadrados (m²). Para calcular el área de una figura, existen fórmulas predefinidas que podemos usar.
A continuación, aprenderemos sobre el área de un cuadrado, conoceremos su fórmula y la usaremos para resolver algunos ejercicios.
¿Cómo se calcula el área de un cuadrado?
El área es el espacio cubierto por el objeto, es decir, es la región ocupada por cualquier figura. Cuando medimos el área de un cuadrado, solo considerados la longitud de uno de sus lados, ya que todos sus lados son iguales.
Para calcular el área de un cuadrado, simplemente elevamos al cuadrado a la longitud de uno de sus lados:
$latex A={{l}^2}$
aquí,
- A representa al área del cuadrado
- l representa a la longitud de uno de los lados del cuadrado
Miremos por qué esta fórmula es verdadera graficando a un cuadrado. Queremos encontrar el área de un cuadrado que tiene lados de longitud 5 cm. Usando esta dimensión, dibujamos a un cuadrado en un papel que tiene una cuadrícula de 1 cm × 1 cm.
El cuadrado que dibujamos cubre 25 de estos cuadrados pequeños.
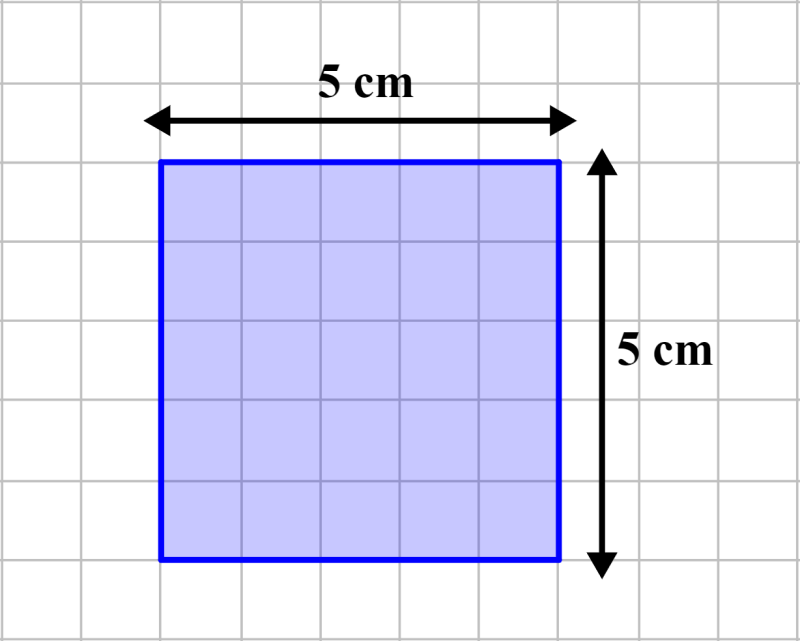
Entonces, el área del cuadrado es 25 cm², lo cual puede ser escrito como 5 cm × 5 cm, es decir, tenemos lado × lado. Entonces, tenemos que el área del cuadrado es:
| Área = Lado × Lado Área = Lado² $latex A={{l}^2}$ |
Las siguientes son algunas conversiones de unidades que podrían resultar útiles:
- 1 m = 100 cm
- 1 m² = 10 000 cm²
- 1 km = 1000 m
- 1 km² = 1 000 000 m²
Ejercicios de área de un cuadrado resueltos
Los siguientes ejercicios son resueltos usando la fórmula del área de un cuadrado detallada arriba. Intenta resolver los ejercicios tú mismo antes de mirar la solución.
EJERCICIO 1
Encuentra el área de un cuadrado que tiene lados de longitud 12 m.
Solución
Tenemos que la longitud de un lado del cuadrado es 12 m.
Podemos usar la fórmula $latex A={{l}^2}$ con el valor dado:
$latex A={{l}^2}$
$latex A={{12}^2}$
$latex A=144$
Entonces, el área del cuadrado es 144 m².
EJERCICIO 2
¿Cuál es el área de un cuadrado que tiene lados de longitud 15 cm?
Solución
En este caso, la longitud de un lado del cuadrado es 15 cm.
Tenemos la fórmula $latex A={{l}^2}$, por lo que reemplazamos a l con el valor dado:
$latex A={{l}^2}$
$latex A={{15}^2}$
$latex A=225$
Entonces, el área del cuadrado es 225 cm².
EJERCICIO 3
Una pared cuadrada tiene lados de longitud 6 m. ¿Cuál es el costo de pintar a una tasa de 0.5 dólares por metro cuadrado?
Solución
Tenemos que calcular el área de la pared para saber cuántos metros cuadrados tenemos que pintar.
Entonces, usamos la fórmula $latex A={{l}^2}$ con una longitud de 6 m:
$latex A={{l}^2}$
$latex A={{6}^2}$
$latex A=36$
El área de la pared es 36 metos cuadrados. Si es que la tasa es 0.5 dólares por metro cuadrado, el costo será:
$latex 36\times 0.5=18$ dólares
EJERCICIO 4
¿Cuál es la longitud de los lados de un cuadrado que tiene un área de 121 cm²?
Solución
En este caso, tenemos que calcular la longitud de los lados partiendo desde el área. Usamos la fórmula del área y sacamos la raíz cuadrada de ambos lados para obtener la longitud de un lado:
$latex A={{l}^2}$
$latex 121={{l}^2}$
$latex l=\sqrt{121}$
$latex l=11$
Entonces, la longitud de un lado del cuadrado es 11 cm.
EJERCICIO 5
Un piso cuadrado que tiene lados de longitud 40 m va a ser cubierto de cerámica. Si es que cada cerámica tiene lados de longitud 2 m, ¿cuántas cerámicas se necesitan para cubrir el piso?
Solución
Tenemos que encontrar tanto el área del piso, como el área de cada cerámica. Entonces, el área del piso es:
$latex A_{p}={{l_{p}}^2}$
$latex A_{p}={{40}^2}$
$latex A_{p}=1600$
El área del piso es 1600 m² y el área de cada cerámica es:
$latex A_{c}={{l_{c}}^2}$
$latex A_{c}={{2}^2}$
$latex A_{c}=4$
El área de cada cerámica es 4 m². Entonces, necesitamos:
$latex \frac{A_{p}}{A_{c}}=\frac{1600}{4}=400$ cerámicas
Ejercicios de área de un cuadrado para resolver
Pon en práctica lo aprendido sobre el área de un cuadrado para resolver los siguientes ejercicios. Selecciona una respuesta y haz clic en “Verificar” para comprobar que escogiste la correcta. Mira los ejercicios resueltos de arriba en caso de necesitar ayuda.
Véase también
¿Interesado en aprender más sobre cuadrados? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
