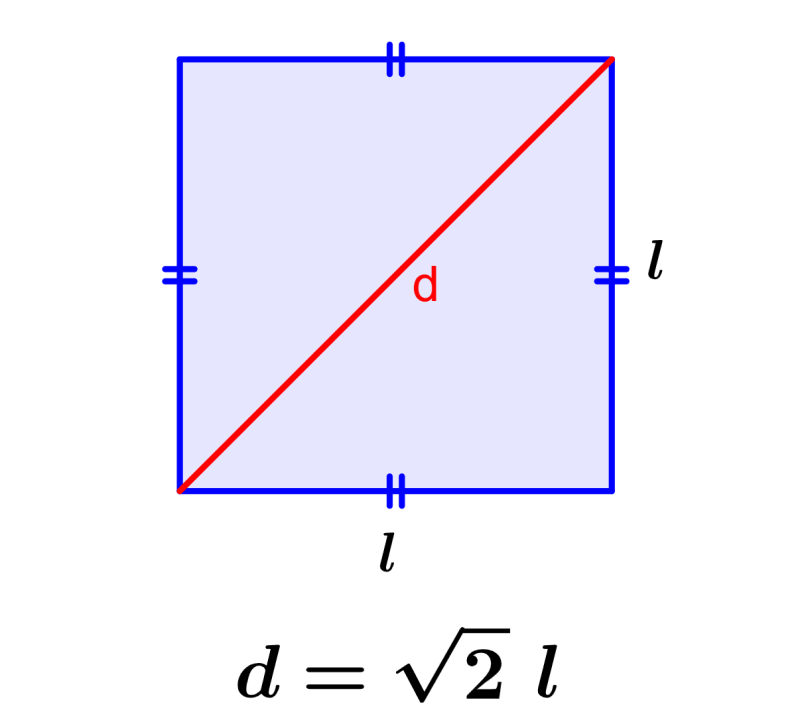
En geometría, un cuadrado es un cuadrilátero regular, el cual tiene cuatro lados de igual longitud y cuatro ángulos que miden 90 grados. Un cuadrado puede tener dos diagonales. Cada una de las diagonales puede ser formada al unir los vértices del cuadrado que son diagonalmente opuestos. La longitud de la diagonal de un cuadrado puede ser calculada al usar el teorema de Pitágoras. El teorema de Pitágoras es simplificado al reconocer que las longitudes de los lados requeridos son iguales.
A continuación, conoceremos la fórmula que puede ser usada para calcular la longitud de la diagonal de un cuadrado. Además, veremos algunos ejercicios en los que usaremos esta fórmula.
¿Cómo calcular la diagonal de un cuadrado?
Podemos calcular la diagonal de un cuadrado usando una fórmula derivada del teorema de Pitágoras. Consideremos a un cuadrado ABCD que tiene lados de longitud “l” cm.
Vemos que las líneas AD y BC son las diagonales del cuadrado:
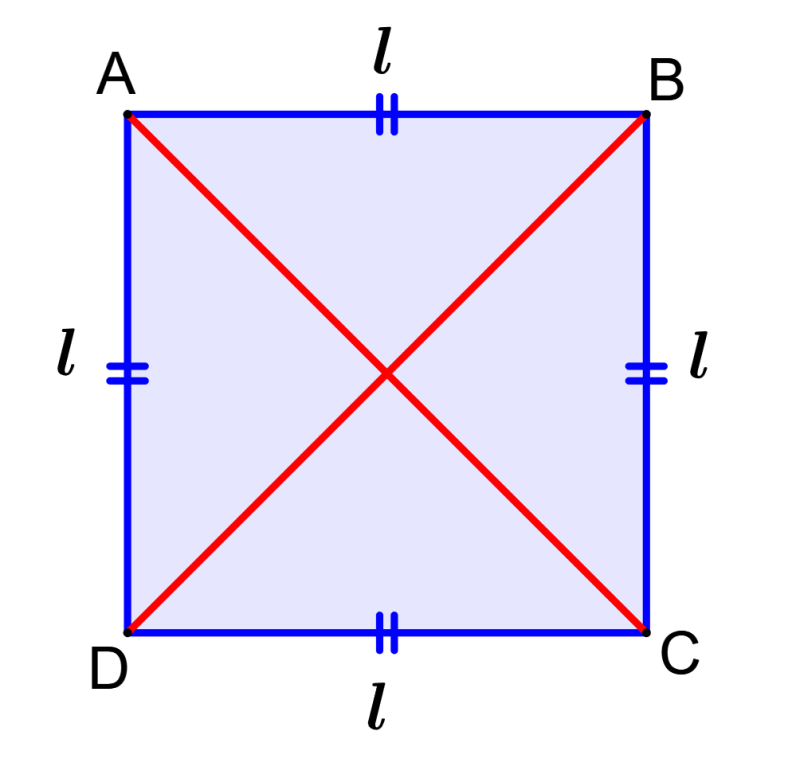
Claramente podemos ver que una diagonal divide al cuadrado en dos triángulos iguales $latex \Delta ACD$ y $latex \Delta BDC$. Vamos a usar a uno de los triángulos para calcular la longitud de la diagonal.
Podemos aplicar el teorema de Pitágoras en $latex \Delta ACD$ para obtener la longitud de la diagonal. Entonces, tenemos:
$latex {{AC}^2}={{AD}^2}+{{CD}^2}$
Sabemos que $latex AD=CD=l$. Entonces, podemos sustituir esto en la ecuación de arriba:
$latex {{AC}^2}={{l}^2}+{{l}^2}$
$latex {{AC}^2}=2{{l}^2}$
$latex AC=\sqrt{2}~l$
Entonces, la longitud de la diagonal de un cuadrado es:
| $latex d=\sqrt{2}~l$ |
Las propiedades de las diagonales de los cuadrados son las siguientes:
- Ambas diagonales son congruentes (tienen la misma longitud).
- Ambas diagonales bisecan la una a la otra, es decir, el punto en el que las diagonales se cruzan es el punto medio.
- Una diagonal divide al cuadrado en dos triángulos rectángulos isósceles.
Ejercicios de diagonal de un cuadrado resueltos
Los siguientes ejercicios son resueltos usando la fórmula de la diagonal indicada arriba. Intenta resolver los ejercicios tú mismo antes de mirar la solución.
EJERCICIO 1
Un cuadrado tiene lados de longitud 12 m. ¿Cuál es la longitud de su diagonal?
Solución
Tenemos que la longitud de los lados del cuadrado es 12 m. Entonces, podemos encontrar su diagonal de la siguiente manera:
$latex d=\sqrt{{{lado}^2}+{{lado}^2}}$
$latex d=\sqrt{2{{lado}^2}}$
$latex d=lado\sqrt{2}$
$latex d=12\sqrt{2}$
Entonces, la diagonal mide $latex 12\sqrt{2}$ m.
EJERCICIO 2
¿Cuál es la longitud de la diagonal un cuadrado que tiene lados de longitud 17 cm?
Solución
La longitud de la diagonal del cuadrado es 17 cm. Entonces, su diagonal puede ser calculada de la siguiente manera:
$latex d=\sqrt{{{lado}^2}+{{lado}^2}}$
$latex d=\sqrt{2{{lado}^2}}$
$latex d=lado\sqrt{2}$
$latex d=17\sqrt{2}$
Entonces, la diagonal del cuadrado tiene una longitud de $latex 17\sqrt{2}$ cm.
EJERCICIO 3
Encuentra la longitud de la diagonal de un cuadrado que tiene lados de longitud 25 cm.
Solución
La diagonal de un cuadrado es calculada usando el teorema de Pitágoras con las longitudes de sus lados. En este caso, los lados del cuadrado tienen una longitud de 25 cm:
$latex d=\sqrt{{{lado}^2}+{{lado}^2}}$
$latex d=\sqrt{2{{lado}^2}}$
$latex d=lado\sqrt{2}$
$latex d=25\sqrt{2}$
Entonces, la diagonal del cuadrado mide $latex 25\sqrt{2}$ cm.
EJERCICIO 4
Tenemos que la diagonal de un cuadrado mide $latex 31\sqrt{2}$ m. ¿Cuál es la longitud de sus lados?
Solución
En este caso, partimos de la diagonal y queremos encontrar la longitud de los lados. Entonces, usamos la fórmula de la diagonal y resolvemos para el lado:
$latex d=lado\sqrt{2}$
$latex 31\sqrt{2}=lado\sqrt{2}$
$latex lado=31$
Entonces, la longitud de los lados del cuadrado es 31 m.
EJERCICIO 5
La diagonal de un cuadrado mide $latex 19\sqrt{2}$ cm. ¿Cuál es la longitud de sus lados?
Solución
Usamos la fórmula de la diagonal, reemplazamos el valor de la diagonal y resolvemos para el lado:
$latex d=lado\sqrt{2}$
$latex 19\sqrt{2}=lado\sqrt{2}$
$latex lado=19$
Entonces, la longitud de los lados del cuadrado es 19 cm.
Ejercicios de diagonal de un cuadrado para resolver
Los siguientes ejercicios pueden ser usados para practicar el uso de la fórmula de la diagonal de un cuadrado. Resuelve los ejercicios y selecciona tu respuesta. Haz clic en “Verificar” para comprobar que seleccionaste la respuesta correcta.
Véase también
¿Interesado en aprender más sobre cuadrados? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
