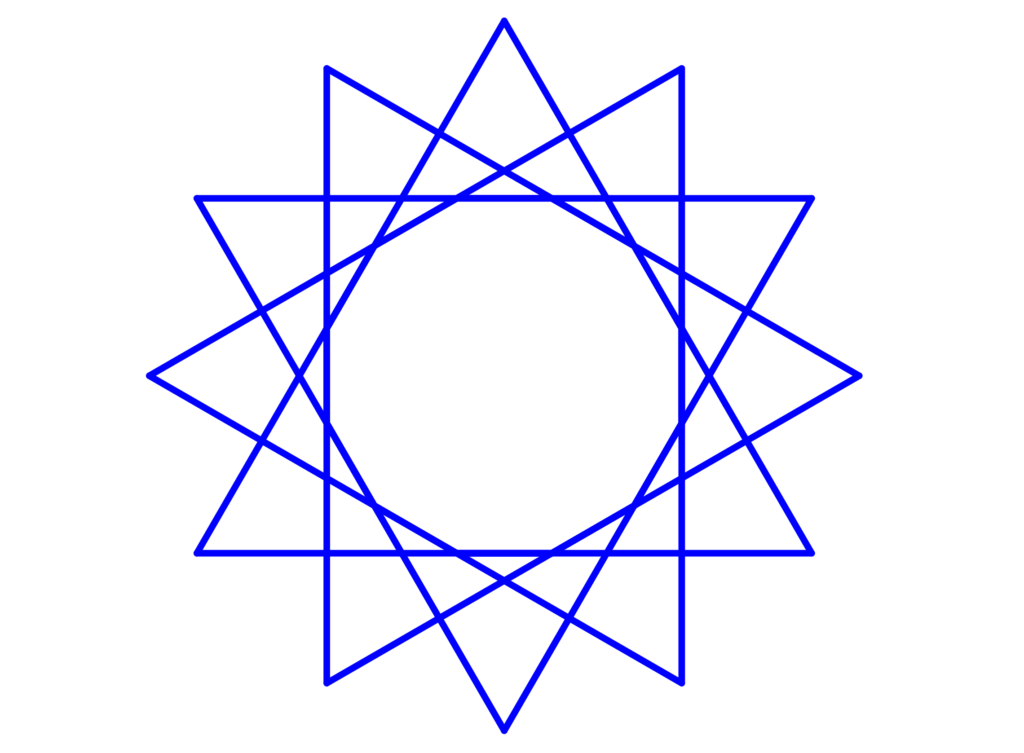
Los polígonos estrellados son formados cuando extendemos los lados de un polígono y esos lados intersecan los unos con los otros. El número de veces que los lados intersecan fuera del polígono determina el grado del polígono estrellado.
A continuación, aprenderemos más detalles sobre los polígonos estrellados. Usaremos diagramas y varios ejemplos para entender los conceptos.
Proceso de estelación
Estelación es el proceso de construir poliedros al extender los lados de los polígonos hasta que se crucen. Si es que los lados nunca se intersecan en un punto fuera del polígono, el polígono no puede ser estelado.
Por ejemplo, la estelación de un hexágono regular se muestra en la siguiente imagen.
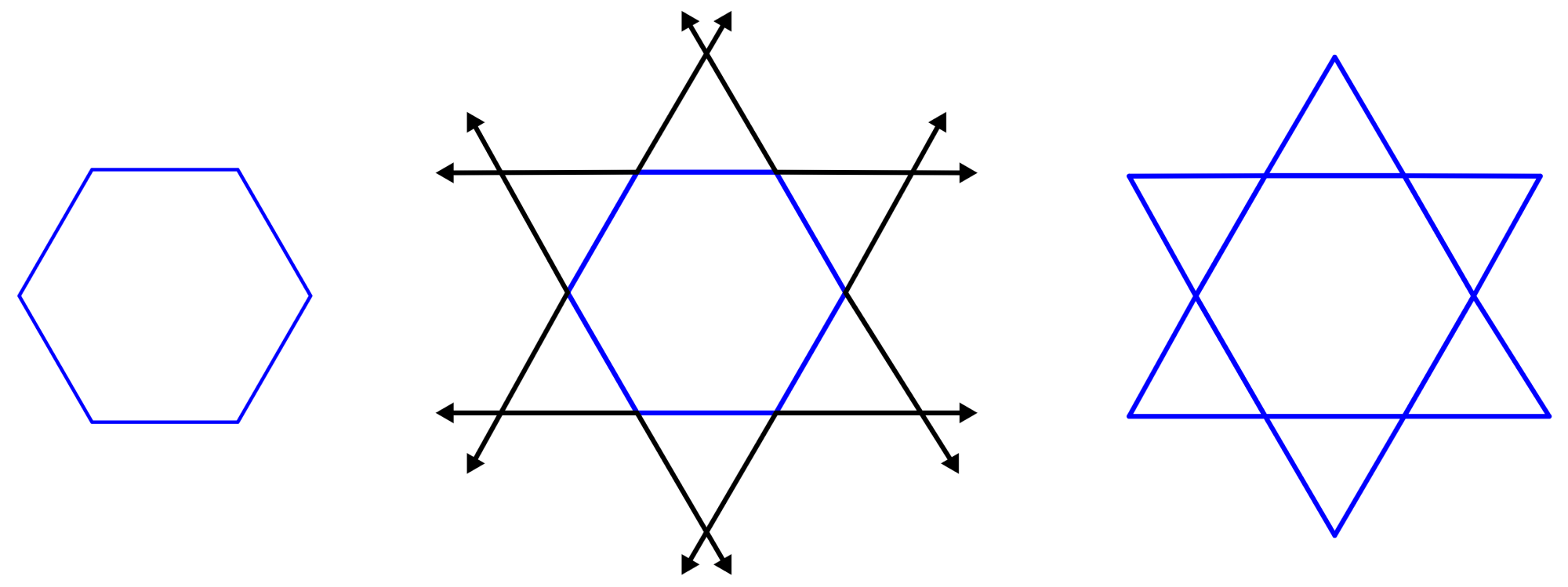
Ahora, pensemos en cuál de los siguientes polígonos no puede ser estelado:
• Cuadrado
• Pentágono regular
• Octágono regular
• Decágono regular
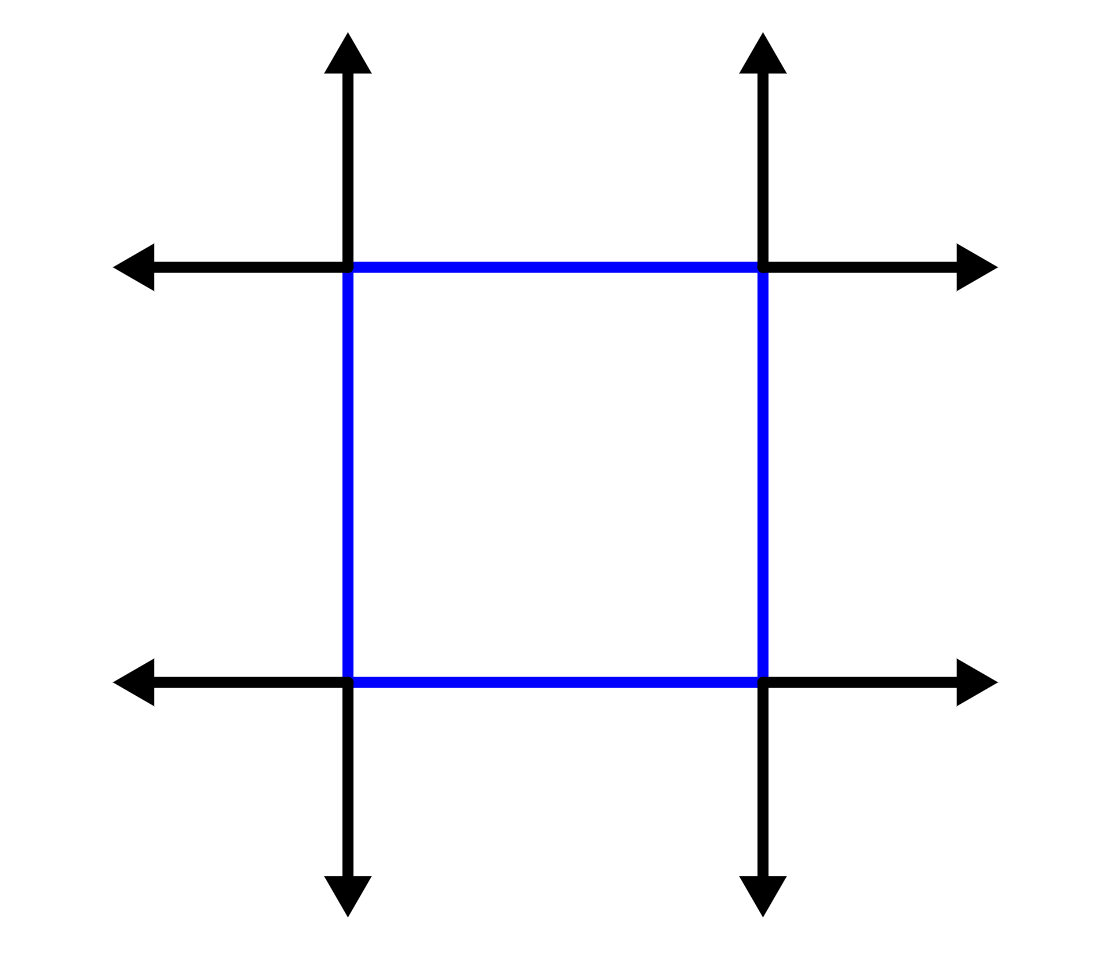
La respuesta es un cuadrado. Al extender los lados de un cuadrado, formamos líneas paralelas que nunca se cruzan en un punto.
Estelaciones de n orden
Una estelación de primer orden de un polígono extiende los lados hasta que las líneas se cruzan por primera vez fuera del polígono. Una estelación de n orden extiende los lados de un polígono hasta que las líneas intersecan n veces en cada dirección.
Por ejemplo, el siguiente diagrama muestra una estelación de segundo orden, ya que las líneas que salen del polígono se intersecan dos veces.
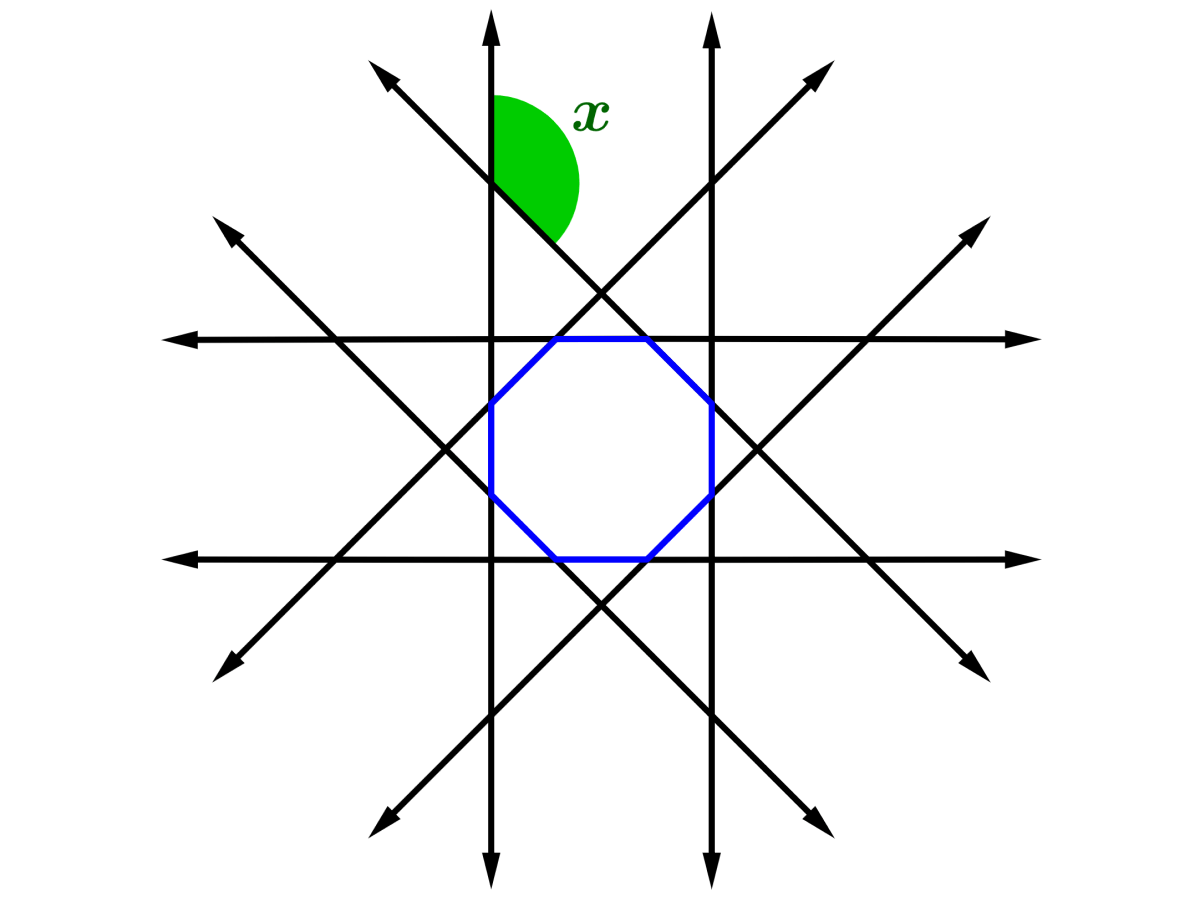
Podemos determinar la medida del ángulo x usando el siguiente diagrama:
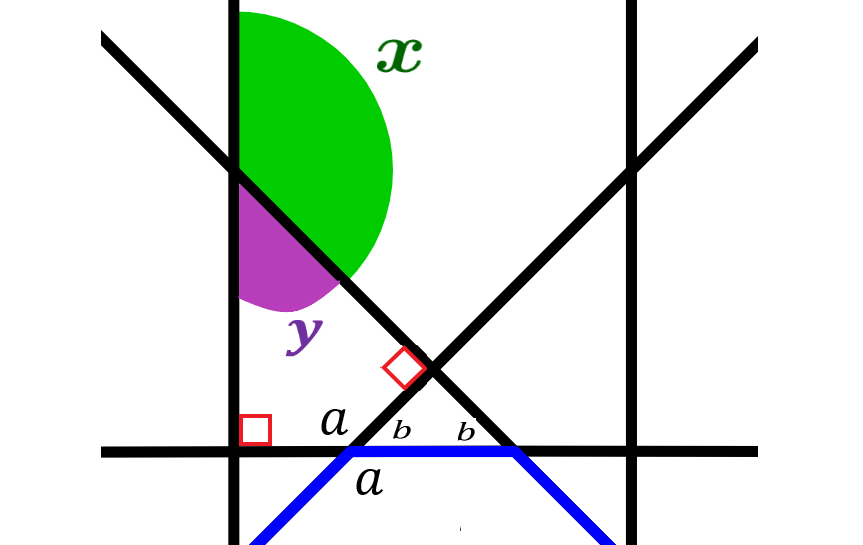
Dado que el octágono es regular, los ángulos interiores del octágono miden 135°. Entonces, en el diagrama tenemos que a=135°. Dado que a y b son una pareja lineal, b=180°-135°=45°. Esto implica que cada triángulo de la estelación es un triángulo isósceles rectángulo, con ángulos rectos.
Los ángulos de un cuadrilátero suman 360°, por lo tanto, y=360°-90°-90°-135°=45°.
Finalmente, dado que y y x son una pareja lineal, tenemos x=180°-45°=135°.
Ahora, veamos otras formas de formar polígonos estrellados. Si es que empezamos con un cuadrado y luego colocamos un cuadrado congruente rotado por 45°, generaremos un octágono estelado de primer orden.
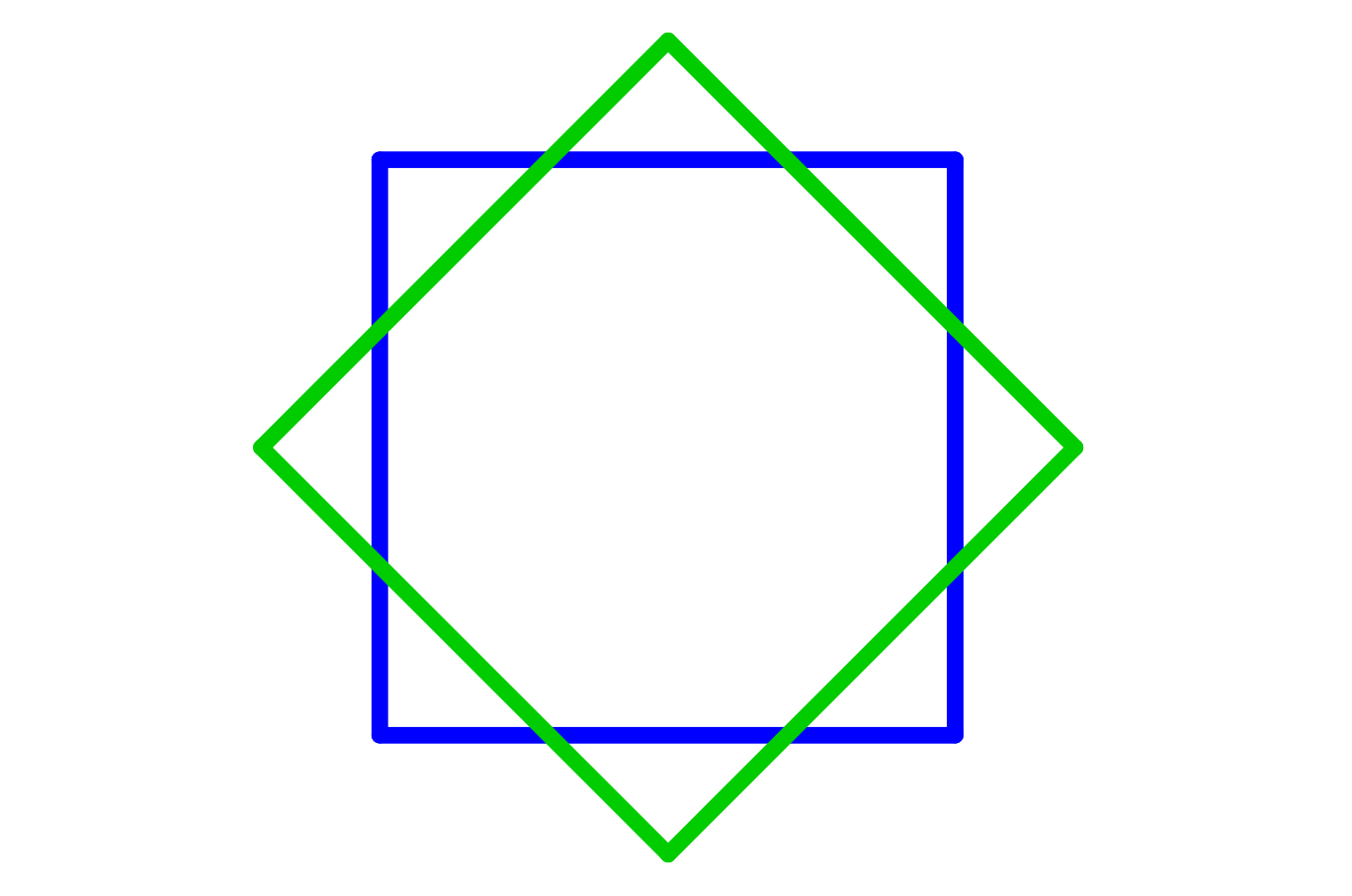
Si es que empezamos con un triángulo equilátero y colocamos múltiples copias rotadas por 30° formaremos un dodecágono (12 lados). Si es que rotamos 30°, después de 120° de rotación, el triángulo estará sobreponiéndose en el triángulo original. Eso significa que hay (120°)/(30°)=4 triángulos equiláteros, los cuales forman un polígono con 3×4=12 lados.
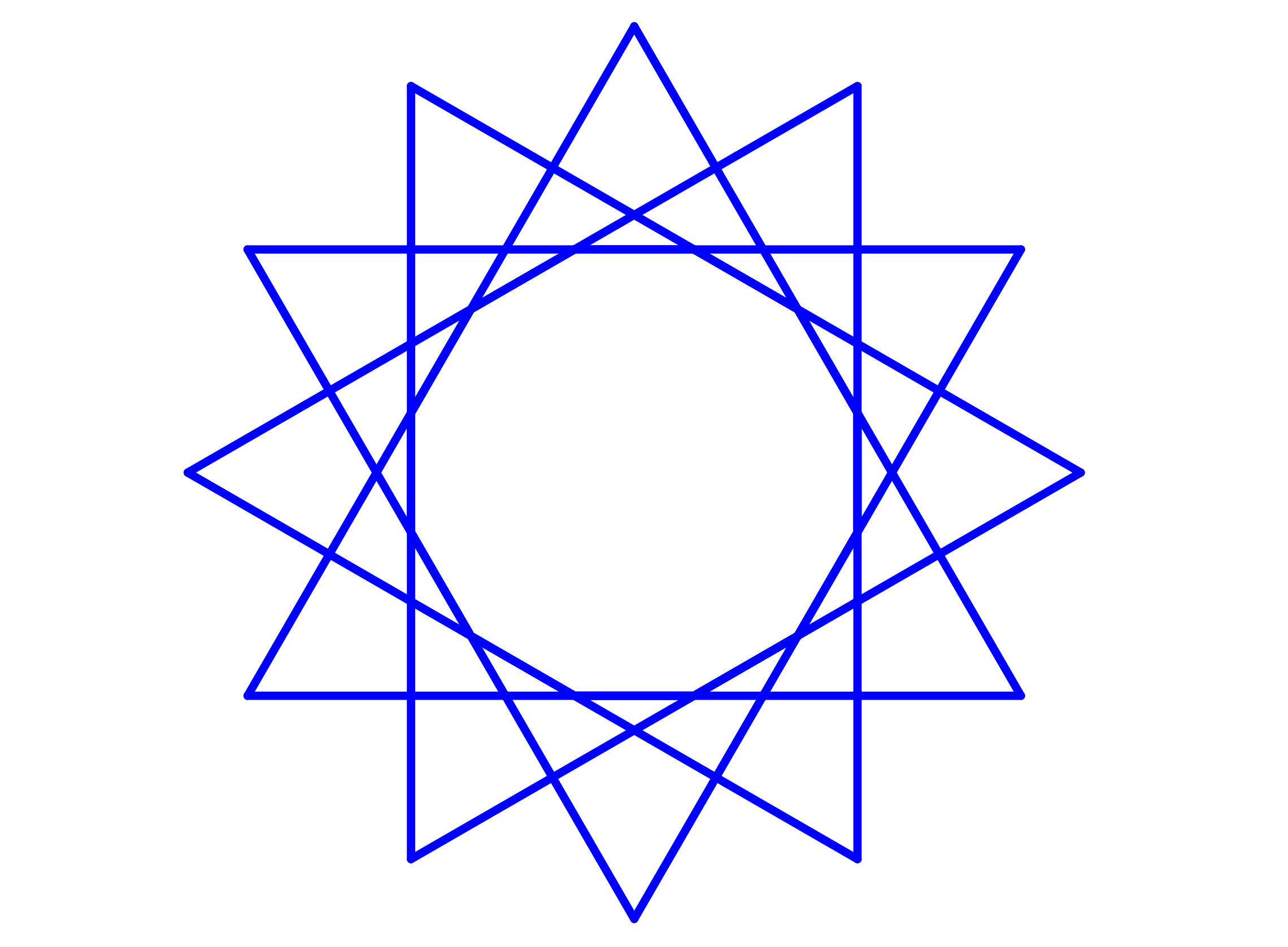
La figura es un polígono estelado de tercer orden, ya que las puntas de los triángulos están en la tercera intersección.
Ejemplos de polígonos estrellados
EJEMPLO 1
La siguiente imagen es un polígono regular con área A, y ese mismo hexágono es estelado para formar una estrella. ¿Cuál es el área de la estrella?
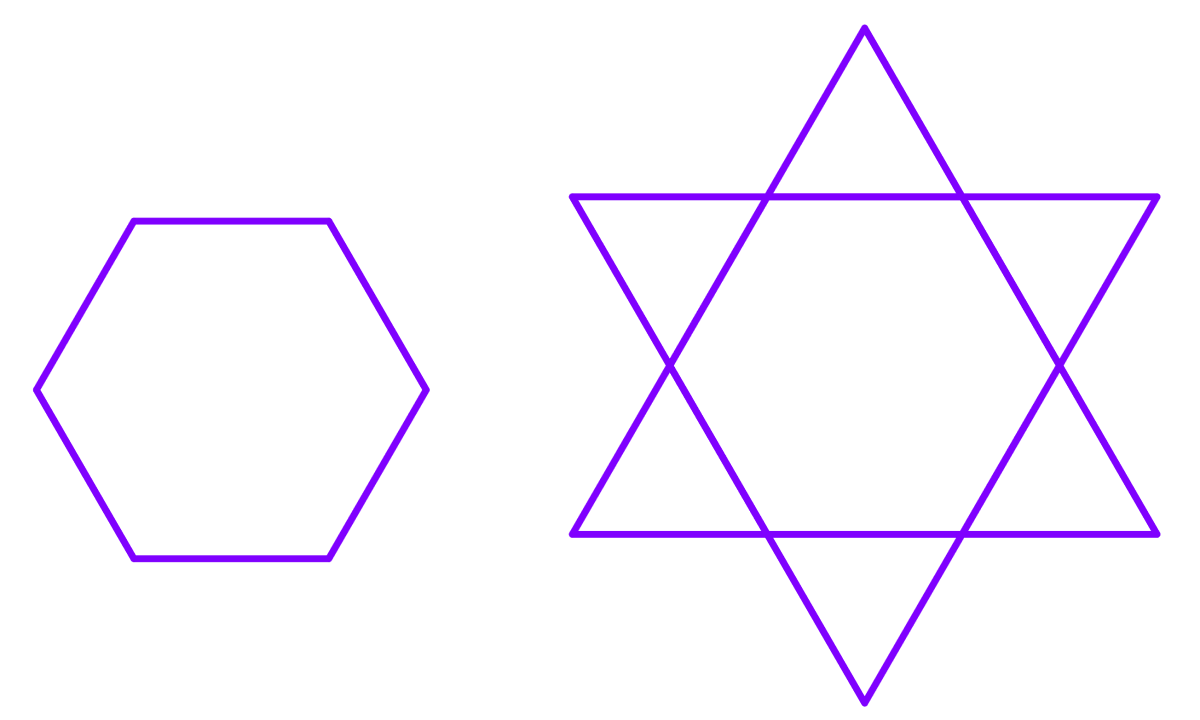
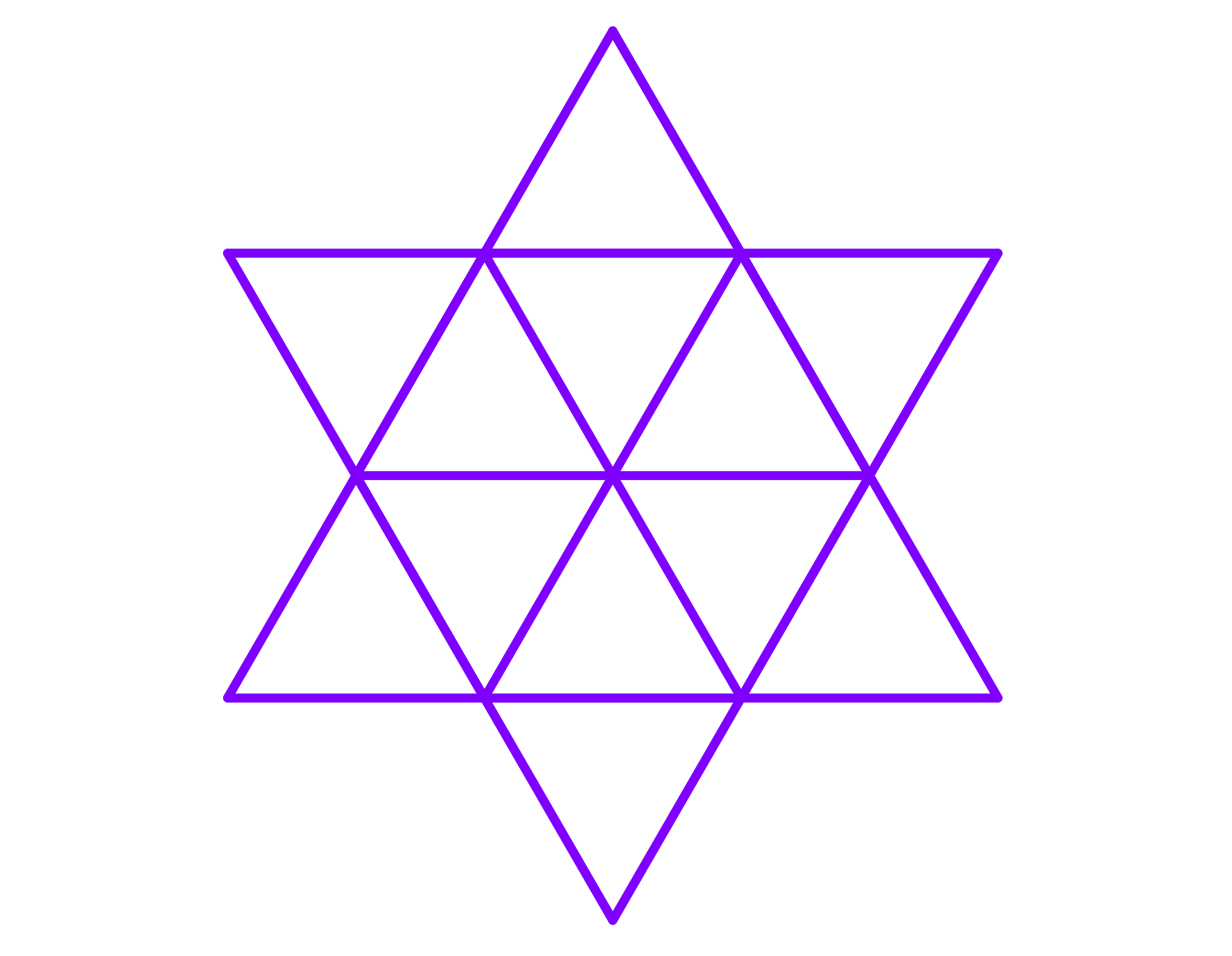
Solución: Un hexágono regular puede ser dividido en triángulos equiláteros. Todos los ángulos serán de 60°.
Las estelaciones también son triángulos equiláteros. Dado que cada ángulo del hexágono regular original es $latex \frac{((6-2)180^{\circ})}{6}=120$°, los ángulos de los triángulos exteriores deben ser 180°-120°=60°.
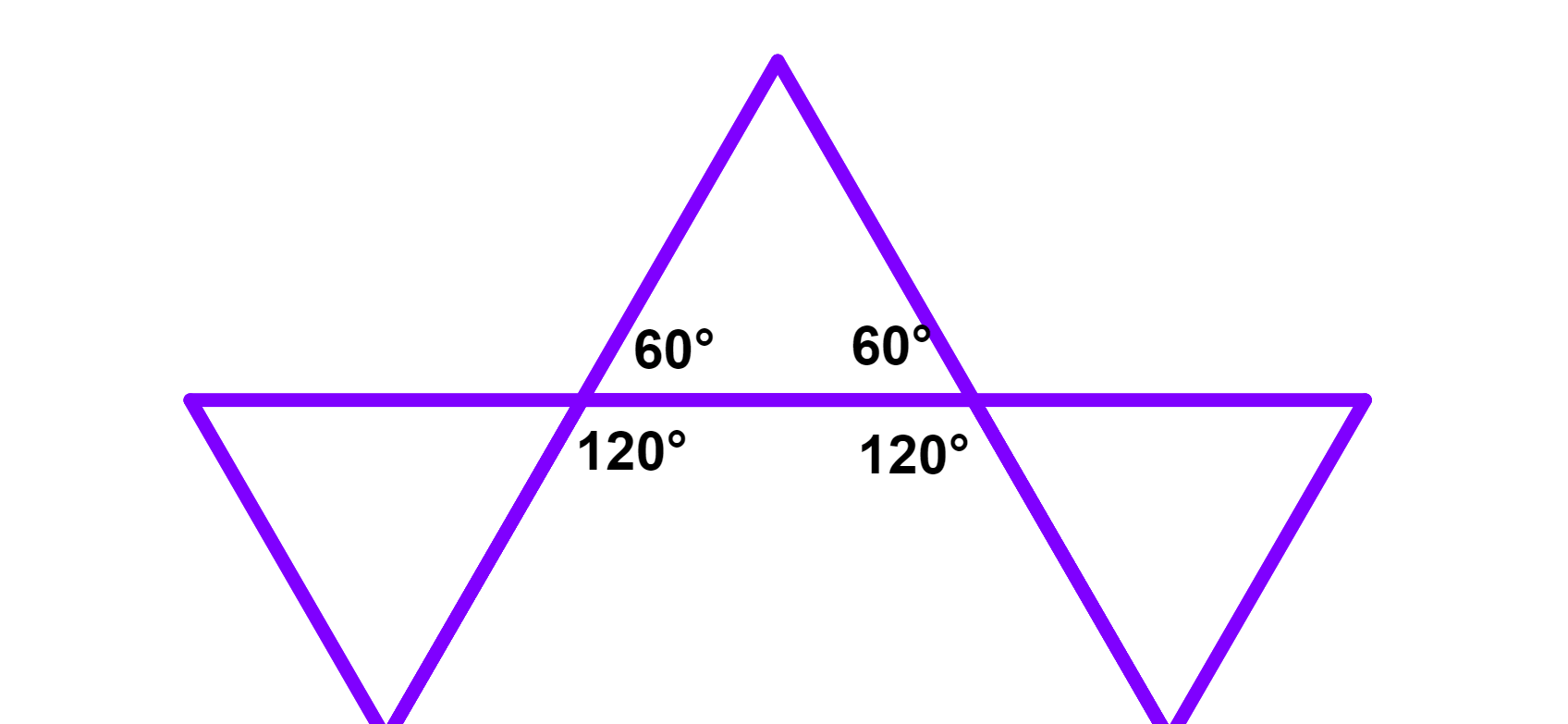
Dado que los triángulos son iguales, el área del pentágono original y la suma de áreas de los triángulos exteriores son las mismas. Entonces, el área total es 2A.
EJEMPLO 2
¿Qué fracción del área total del pentágono estelado representa la región verde?
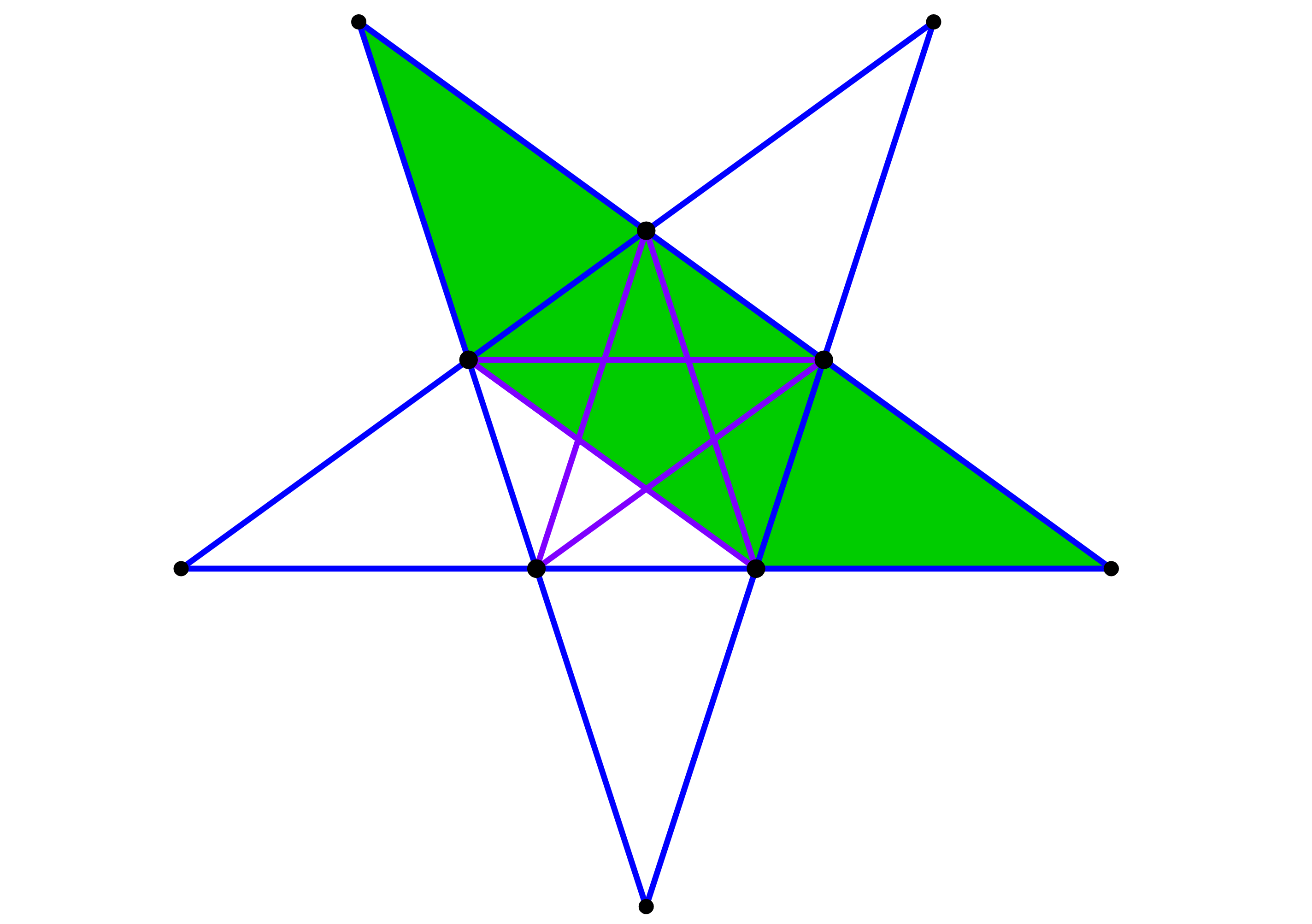
Solución: Cada parte de la figura en la región verde tiene una parte congruente en la región blanca. Estas partes están marcadas en la figura.
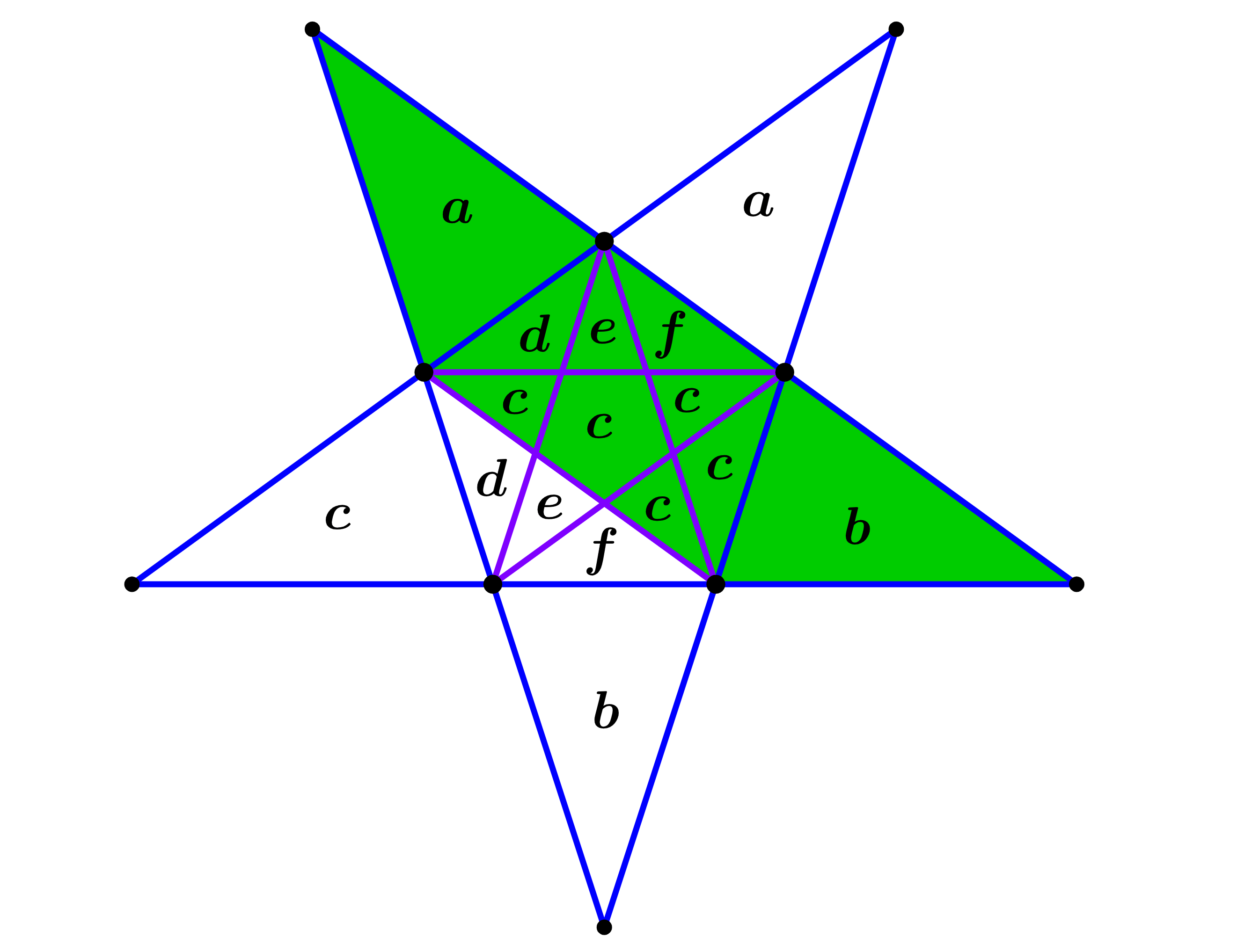
Debido a esto, el área de la región verde es exactamente la mitad del área de la figura entera.
EJEMPLO 3
Un octágono regular con perímetro de 8 unidades es estelado para formar una estrella como se muestra en la siguiente imagen. ¿Cuál es el perímetro de la estrella?
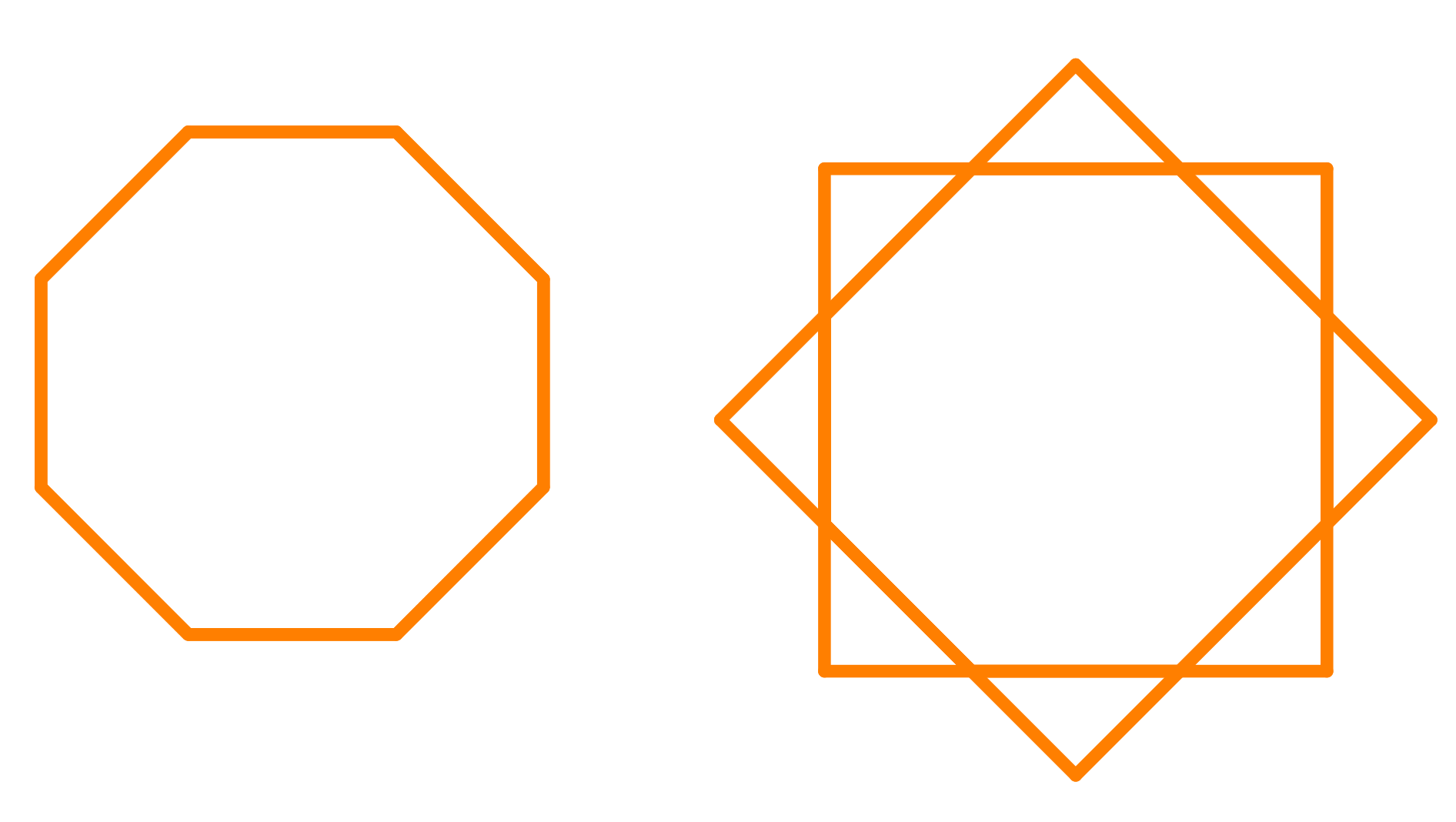
Solución: 8√2
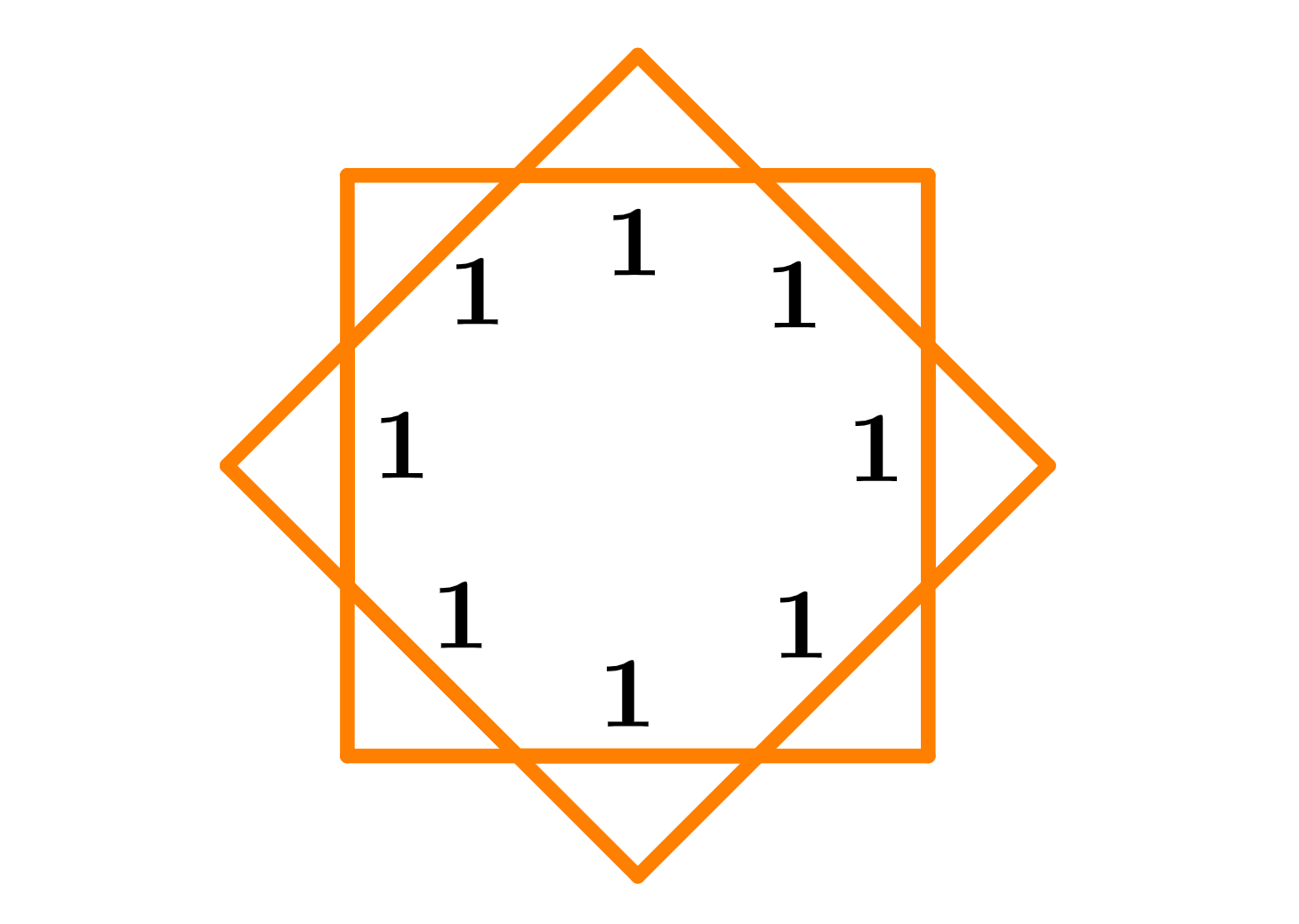
Dado que el octágono es regular, cada uno de los triángulos exteriores es un triángulo rectángulo isósceles con una hipotenusa de 8/8=1.
Los lados de la estrella son congruentes. Podemos usar x para representar la longitud de sus lados y usando el teorema de Pitágoras, tenemos:
$latex {{x}^2}+{{x}^2}={{1}^2}$
$latex {{2x}^2}=1$
$latex {{x}^2}=\frac{1}{2}$
$latex x=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}$
Dado que la estrella tiene 16 lados, significa que el perímetro es $latex 16\times \frac{\sqrt{2}}{2}=8\sqrt{2}$.
Véase también
¿Interesado en aprender más sobre figuras geométricas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
