Las figuras semejantes se caracterizan por tener siempre la misma forma, pero no el mismo tamaño. Estas figuras tienen ángulos iguales, pero no lados iguales. Las proporciones de los lados correspondientes de las figuras semejantes se llama el factor de escala y puede ser usado para describir que tan grande o tan pequeña es una figura en comparación con la otra.
A continuación, aprenderemos sobre las figuras semejantes y sus factores de escala en más detalle.
GEOMETRÍA
Relevante para…
Aprender sobre las figuras semejantes y factores de escala.
GEOMETRÍA
Relevante para…
Aprender sobre las figuras semejantes y factores de escala.
Definición de las figuras semejantes
Dos o más figuras son consideradas semejantes cuando tienen la misma forma. Las figuras semejantes pueden tener el mismo tamaño o una puede ser más grande que la otra.
Usamos el símbolo «~» para indicar que dos figuras son semejantes. Por ejemplo, si es que los triángulos ABC y DEF son semejantes, podemos escribir:
ΔABC ~ ΔDEF
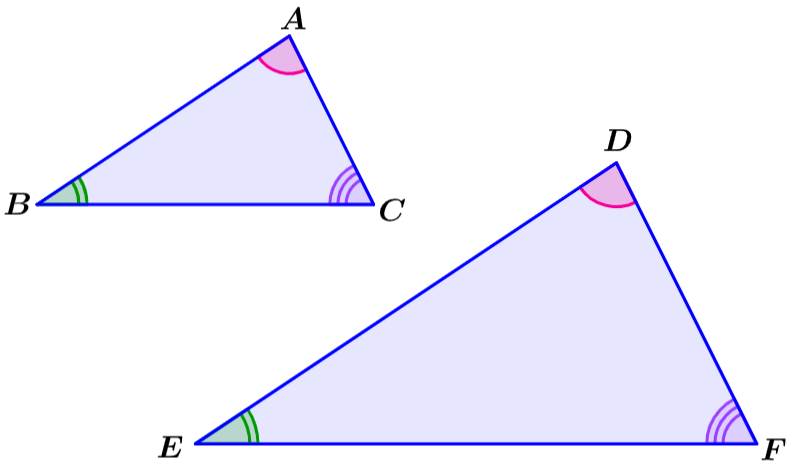
Dado que la forma de las figuras semejantes es la misma, sus ángulos correspondientes también serán los mismos. Podemos usar la declaración de semejanza para determinar cuáles ángulos son iguales.
Por ejemplo, en el ejemplo de arriba, los águlos A y D son iguales, ya que están escritos en primer orden. De igual forma, los ángulos B y E también son iguales, al igual que los ángulos C y F.
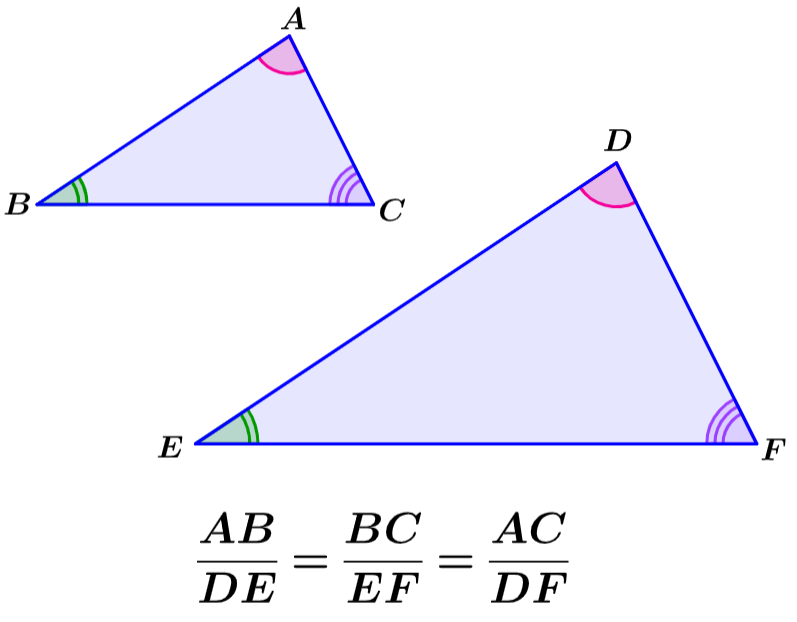
Las figuras semejantes pueden tener lados que tienen diferentes tamaños, por lo que las longitudes correspondientes no son necesariamente las mismas. Sin embargo, las proporciones de los ángulos correspondientes siempre son las mismas. Por ejemplo, en las siguientes figuras semejantes, tenemos las proporciones:
Ahora, si es que dividimos todos los lados correspondientes de las siguientes figuras semejantes, siempre obtenemos 1/2. Para que dos figuras sean semejantes, las proporciones de sus lados correspondientes deben ser las mismas.
¿Qué son los factores de escala?
Los factores de escala son las proporciones que obtenemos cuando dividimos las longitudes de los lados correspondientes de figuras semejantes. En el ejemplo que vimos arriba, todas las proporciones simplifican a 1/2, por lo que tenemos que el factor de escala del triángulo ABC al triángulo DEF es 1/2.
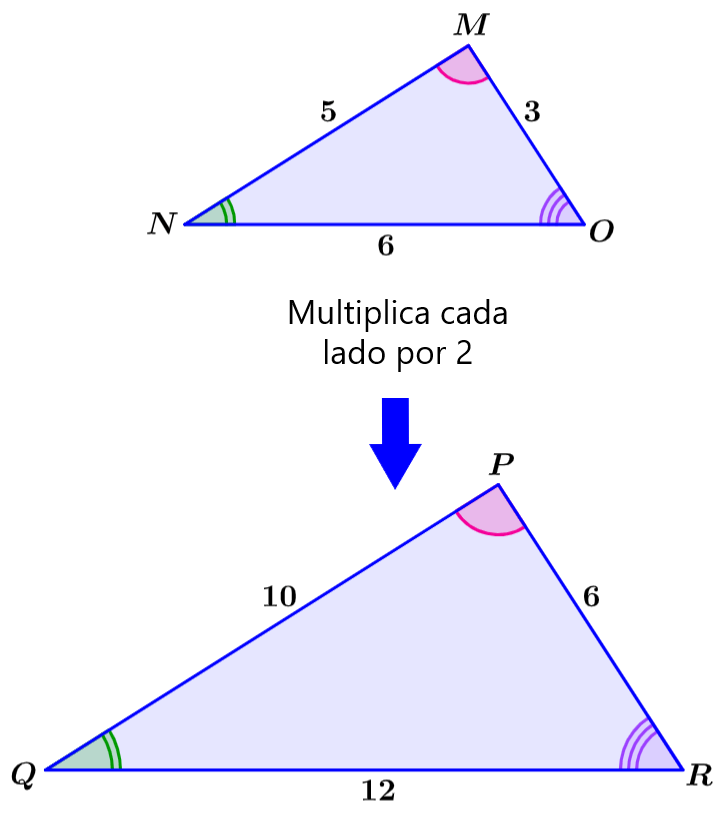
También podemos considerar a los factores de escala como multiplicadores. Por ejemplo, el factor de escala del triángulo MNO al triángulo PQR es 2. Esto significa que el triángulo PQR es el doble de grande que el triángulo MNO.
Si es que multiplicamos por 2 a un lado del triángulo MNO, obtenemos la longitud del lado correspondiente del triángulo PQR. Las proporciones de todos los lados de estos triángulos son iguales a 2. Es decir, tenemos $latex \frac{10}{5}=2$, $latex \frac{12}{6}=2$, $latex \frac{6}{3}=2$.
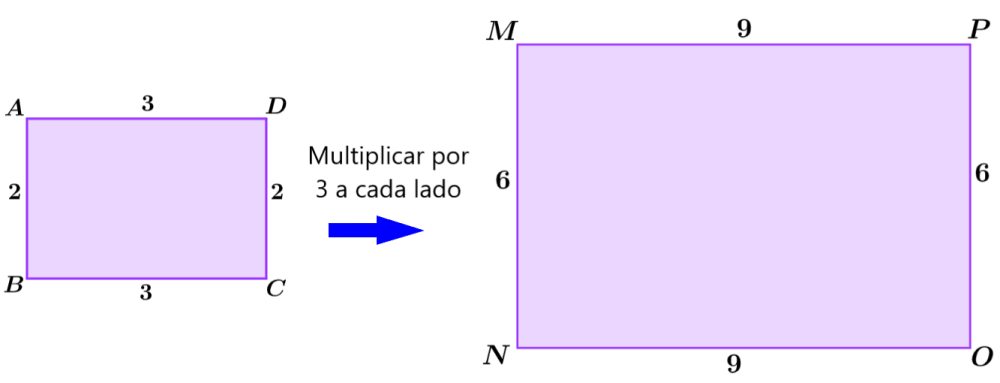
Veamos otro ejemplo. El factor de escala del rectángulo ABCD al rectángulo MNOP es 3. Esto significa que el segundo rectángulo es tres más veces más grande en comparación con el primer rectángulo. Podemos obtener las longitudes de los lados correspondientes del segundo rectángulo al multiplicar a los lados del primer rectángulo por 3.
Ejemplos de factores de escala
EJEMPLO 1
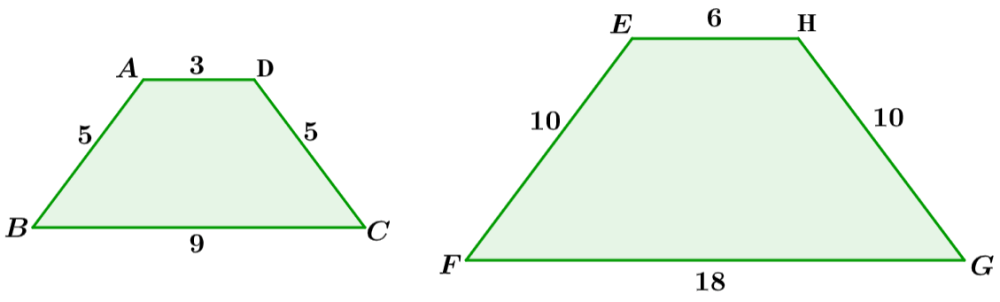
Encuentra el factor de escala del trapecio ABCD al trapecio EFGH.
Solución: En este caso, la figura pequeña fue indicada primero. Dado que la segunda figura es más grande, esto significa que el factor de escala debe ser mayor que 1.
Ahora, comparando las longitudes de los lados correspondientes, podemos deducir que podemos multiplicar por 2 para obtener las mismas longitudes. Entonces, el factor de escala es 2. También podemos encontrar el factor de escala al encontrar las siguientes razones:
$latex \frac{6}{3}=2, ~\frac{10}{5}=2, ~\frac{18}{9}=2$
EJEMPLO 2
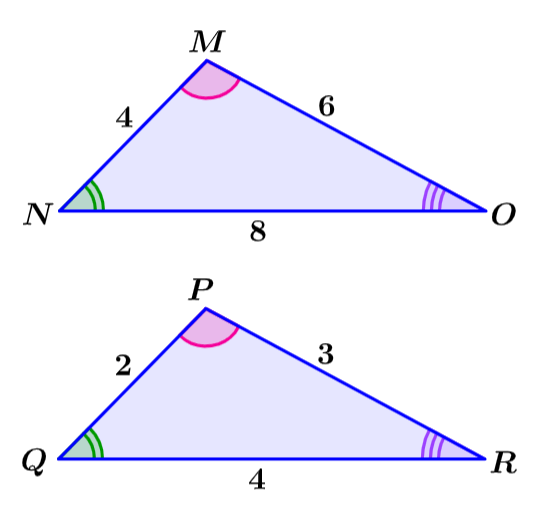
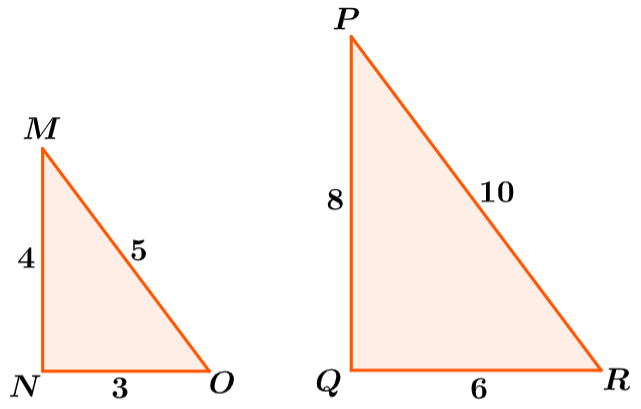
Encuentra el factor de escala del triángulo MNO al triángulo PQR
Solución: El triángulo indicado segundo es más grande que el primero, por lo que sabemos que el factor de escala va a ser mayor que 1. En este caso, el factor de escala no es un número entero, por lo que no podemos determinarlo a simple vista.
Entonces, podemos encontrar las proporciones de los lados correspondientes.
Sabemos que el factor de escala es mayor que 1, por lo que colocamos al número más grande en el numerador de las fracciones. Entonces, tenemos las proporciones:
$latex \frac{8}{4}=2,~\frac{10}{5}=2, ~\frac{6}{3}=2$
Por lo tanto, el factor de escala es 2.
EJEMPLO 3
Encuentra el factor de escala del triángulo PQR al triángulo MNO.
Solución: Este ejemplo es similar al ejemplo anterior con la diferencia que el orden está cambiado. Dado que el segundo triángulo es más pequeño, el factor de escala será menor que 1 en este caso.
Sabemos que el orden simplemente ha sido cambiado, por lo que podemos darle la vuelta a las fracciones para encontrar las proporciones correctas:
$latex \frac{4}{8}=\frac{1}{2}, ~\frac{3}{6}=\frac{1}{2}, \frac{5}{10}=\frac{1}{2}$
Entonces, el factor de escala es $latex \frac{1}{2}$.
Véase también
¿Interesado en aprender más sobre figuras geométricas? Mira estas páginas: