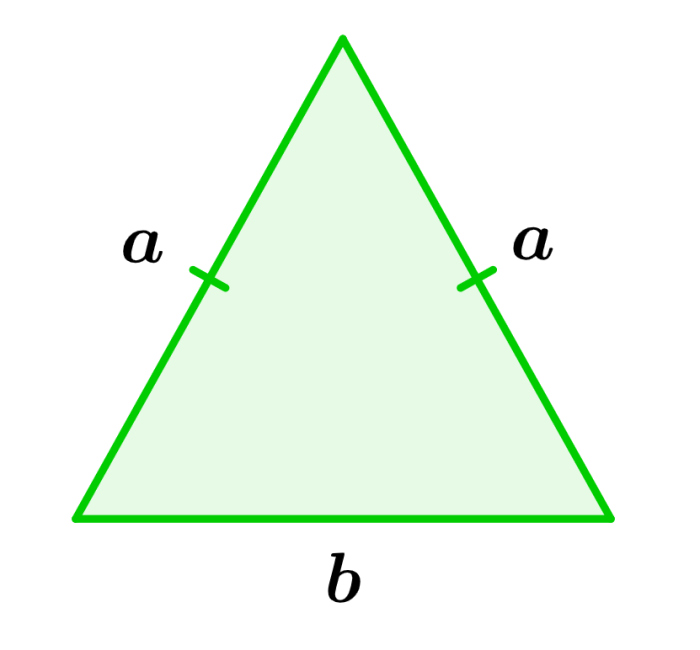
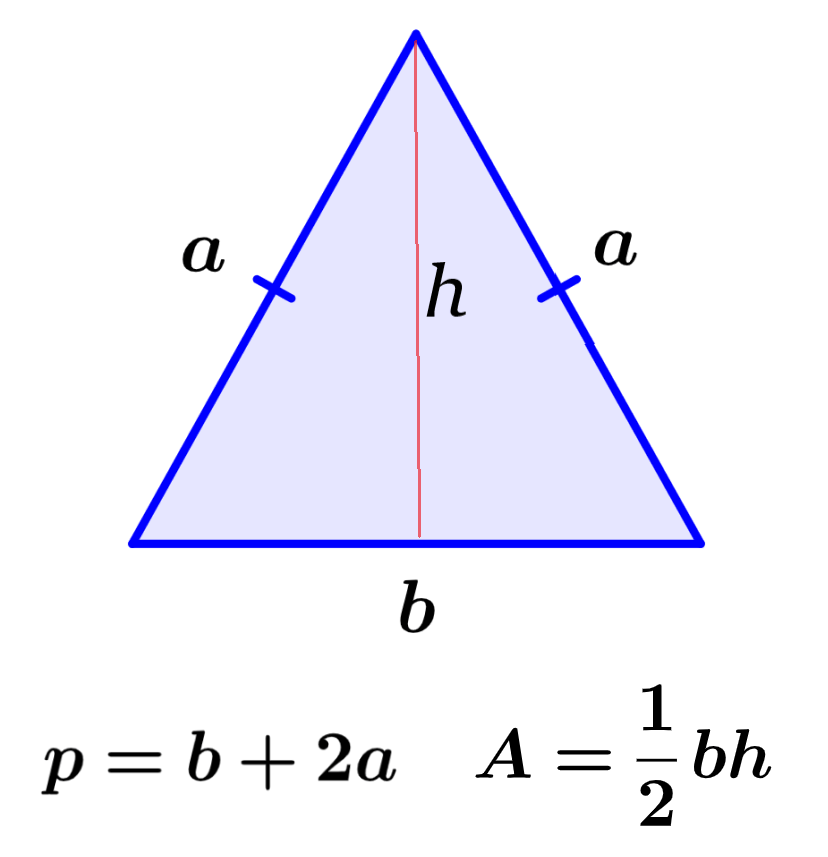El perímetro de un triángulo isósceles representa la longitud total alrededor del triángulo. Por otro lado, el área representa el espacio bidimensional ocupado por la figura. Podemos calcular el perímetro de un triángulo isósceles al sumar las longitudes de sus tres lados y podemos calcular su área al multiplicar por un medio al producto de su base y de su altura.
A continuación, aprenderemos cómo calcular el perímetro y el área de un triángulo isósceles. Conoceremos sus fórmulas y las usaremos para resolver algunos ejercicios de práctica.
GEOMETRÍA
Relevante para…
Aprender sobre el perímetro y el área de un triángulo isósceles.
GEOMETRÍA
Relevante para…
Aprender sobre el perímetro y el área de un triángulo isósceles.
¿Cómo calcular el perímetro de un triángulo isósceles?
Podemos calcular el perímetro de un triángulo isósceles al sumar las longitudes de sus tres lados. Esto significa que podemos usar la siguiente fórmula:
$latex p=a+b+c$
en donde, $latex a,~b,~c$ son las longitudes de los lados del triángulo.
Sin embargo, dado que un triángulo isósceles tiene dos lados con la misma longitud, podemos simplificar la fórmula del perímetro de la siguiente manera:
| $latex p=b+2a$ |
en donde, b es la longitud de la base y a es la longitud de los lados congruentes.
¿Cómo calcular el área de un triángulo isósceles?
Podemos calcular el área de un triángulo isósceles al multiplicar a un medio por el producto de su base y de su altura. Es decir, multiplicamos a las longitudes de su base y de su altura y dividimos por 2:
| $latex \text{Área}= \frac{1}{2} \times \text{base} \times \text{altura}$ $latex A=\frac{1}{2} \times b \times h$ |
en donde, b es la longitud de la base y h es la longitud de la altura.
Calcular el área de un triángulo isósceles si es que solo conocemos sus lados
Para calcular el área de un triángulo isósceles solo en términos de sus lados, tenemos que encontrar una expresión para la altura del triángulo en términos de sus lados y luego sustituirla en la fórmula del área.
La Altura del Triángulo Isósceles puede ser calculada usando la siguiente fórmula:
$latex h=\sqrt{{{a}^2}-\frac{{{b}^2}}{4}}$
Sustituyendo esta expresión para la altura en la fórmula del área, tenemos:
| $latex A=\frac{1}{2}(\sqrt{{{a}^2}-\frac{{{b}^2}}{4}}\times b)$ |
en donde,
- b es la longitud de la base del triángulo isósceles
- h es la altura del triángulo
- a es la longitud de los lados congruentes del triángulo isósceles
Área y perímetro de un triángulo isósceles – Ejercicios resueltos
EJERCICIO 1
Encuentra el perímetro de un triángulo isósceles que tiene una base con una longitud de 11 mm y lados congruentes de 8 mm.
Solución
Tenemos las siguientes longitudes:
- Base, $latex b=11$ mm
- Lados, $latex a=8$ mm
Usando la fórmula del perímetro con estos valores, tenemos:
$latex p=b+2a$
$latex p=11+2(8)$
$latex p=11+16$
$latex p=27$
El perímetro del triángulo es igual a 27 mm.
EJERCICIO 2
Calcula el área de un triángulo isósceles que tiene una base con una longitud de 6 cm y una altura de 7 cm.
Solución
Tenemos la siguiente información:
- Altura, $latex h=7$ cm
- Base, $latex b=6$ cm
Al usar la fórmula del área con estos valores, tenemos:
$latex A= \frac{1}{2} \times b \times h$
$latex A= \frac{1}{2} (6)(7)$
$latex A=21$
El área del triángulo es igual a 21 cm².
EJERCICIO 3
¿Cuál es el perímetro de un triángulo isósceles que tiene una base de 12 m y lados congruentes de 15 m?
Solución
Tenemos las siguientes longitudes:
- Base, $latex b=12$ m
- Lados, $latex a=15$ m
Aplicando la fórmula del perímetro con la información dada, tenemos:
$latex p=b+2a$
$latex p=12+2(15)$
$latex p=12+30$
$latex p=42$
El perímetro del triángulo es igual a 42 m.
EJERCICIO 4
Encuentra el área de un triángulo isósceles que tiene una base con una longitud de 10 mm y una altura de 11 mm.
Solución
Tenemos las siguientes longitudes:
- Altura, $latex h=11$ mm
- Base, $latex b=10$ mm
Reemplazando a estos valores en la fórmula del área, tenemos:
$latex A= \frac{1}{2} \times b \times h$
$latex A= \frac{1}{2} (10)(11)$
$latex A=55$
El área del triángulo es igual a 55 mm².
EJERCICIO 5
¿Cuál es el perímetro de un triángulo isósceles que tiene lados congruentes de 22 cm y una base de 15 cm?
Solución
Podemos observar las siguientes longitudes:
- Base, $latex b=15$ cm
- Lados, $latex a=22$ cm
Usando la fórmula del perímetro con estos valores, tenemos:
$latex p=b+2a$
$latex p=15+2(22)$
$latex p=15+44$
$latex p=59$
El perímetro del triángulo es igual a 59 cm.
EJERCICIO 6
¿Cuál es el área de un triángulo isósceles que tiene una altura de 13 m y una base de 15 m?
Solución
Tenemos las siguientes longitudes:
- Altura, $latex h=13$ m
- Base, $latex b=15$ m
Usando la fórmula del área con estos valores, tenemos:
$latex A= \frac{1}{2} \times b \times h$
$latex A= \frac{1}{2} (15)(13)$
$latex A=97.5$
El área del triángulo es igual a 97.5 m².
EJERCICIO 7
¿Cuál es la longitud de la base de un triángulo isósceles que tiene un perímetro de 38 cm y lados congruentes de 13 cm?
Solución
Tenemos lo siguiente:
- Perímetro, $latex p=38$ cm
- Lados, $latex a=13$ cm
En este caso, conocemos el perímetro del triángulo y queremos encontrar la longitud de la base, por lo que usamos la fórmula del perímetro y resolvemos para b:
$latex p=b+2a$
$latex 38=b+2(13)$
$latex 38=b+26$
$latex b=12$
La longitud de la base es 12 cm.
EJERCICIO 8
¿Cuál es el área de un triángulo isósceles que tiene una base con una longitud de 8 m y sus lados congruentes miden 10 m?
Solución
Tenemos las siguientes longitudes:
- Base, $latex b=8$ m
- Lados congruentes, $latex a=10$ m
Dado que solo conocemos las longitudes de los lados del triángulo y no de su altura, podemos usar la segunda fórmula del área y tenemos:
$latex h=\frac{1}{2}(\sqrt{{{a}^2}-\frac{{{b}^2}}{4}}\times b)$
$latex h=\frac{1}{2}(\sqrt{{{10}^2}-\frac{{{8}^2}}{4}}\times 8)$
$latex h=\frac{1}{2}(\sqrt{100-\frac{64}{4}}\times 8)$
$latex h=\frac{1}{2}(\sqrt{100-16}\times 8)$
$latex h=\frac{1}{2}(\sqrt{84}\times 8)$
$latex h=\frac{1}{2}(9.17\times 8)$
$latex h=\frac{1}{2}(73.36)$
$latex h=36.68$
El área del triángulo es igual a 36.68 m².
EJERCICIO 9
Si es que un triángulo isósceles tiene una base con una longitud de 25 mm y un perímetro de 55 mm, ¿cuál es la longitud de uno de los lados congruentes del triángulo?
Solución
Tenemos lo siguiente:
- Perímetro, $latex p=55$ mm
- Base, $latex b=25$ mm
Podemos usar la fórmula del perímetro y resolver para a:
$latex p=b+2a$
$latex 55=25+2a$
$latex 2a=30$
$latex a=15$
La longitud de uno de los lados congruentes del triángulo es igual a 15 mm.
EJERCICIO 10
¿Cuál es el área de un triángulo isósceles que tiene una base con una longitud de 12 cm y lados congruentes que miden 14 cm?
Solución
Tenemos las siguiente longitudes:
- Base, $latex b=12$ cm
- Lados congruentes, $latex a=14$ cm
Usando la segunda fórmula del área, tenemos:
$latex h=\frac{1}{2}(\sqrt{{{a}^2}-\frac{{{b}^2}}{4}}\times b)$
$latex h=\frac{1}{2}(\sqrt{{{14}^2}-\frac{{{12}^2}}{4}}\times 12)$
$latex h=\frac{1}{2}(\sqrt{196-\frac{144}{4}}\times 12)$
$latex h=\frac{1}{2}(\sqrt{196-36}\times 12)$
$latex h=\frac{1}{2}(\sqrt{160}\times 12)$
$latex h=\frac{1}{2}(12.65 \times 12)$
$latex h=\frac{1}{2}(151.8)$
$latex h=75.9$
El área del triángulo es igual a 75.9 cm².
Área y perímetro de un triángulo isósceles – Ejercicios para resolver
Véase también
¿Interesado en aprender más sobre triángulos isósceles? Mira estas páginas: