La multiplicidad de raíces se refiere al número de veces que cada raíz aparece en un polinomio dado. Determinar la multiplicidad de las raíces de polinomios resulta fácil si es que tenemos la versión factorizada del polinomio. Alternativamente, también es posible determinar la multiplicidad de las raíces al mirar la gráfica del polinomio.
A continuación, aprenderemos sobre la multiplicidad de raíces y conoceremos cómo determinar la multiplicidad de raíces algebraicamente. Además, también aprenderemos a encontrar la multiplicidad de raíces usando las gráficas de los polinomios.
Ceros y multiplicidad de raíces
Las raíces reales de un polinomio corresponden a los interceptos en x de la gráfica del polinomio. Por lo tanto, podemos encontrar información sobre el número de raíces reales de un polinomio al mirar a su gráfica.
De igual forma, podemos determinar cuántas veces la gráfica tocará o cruzará al eje x al mirar a los ceros del polinomio o a la forma factorizada del polinomio.
Un cero o una raíz tiene una multiplicidad, lo cual se refiere al número de veces que su factor asociado aparece en el polinomio. Por ejemplo, la cuadrática $latex (x+2)(x-3)$ tiene las raíces $latex x=-2$ y $latex x=3$, cada una ocurriendo una sola vez.
El polinomio de quinto grado $latex {{(x+2)}^3}{{(x-3)}^2}$ tiene las mismas raíces que tenía la cuadrática, pero en este caso, la raíz $latex x=-2$ tiene una multiplicidad de 3, ya que el factor $latex (x+2)$ aparece tres veces (está elevado al cubo).
De igual forma, la raíz $latex x=3$ tiene una multiplicidad de 2, ya que el factor $latex (x-3)$ aparece dos veces (está elevado al cuadrado).
Si es que tenemos a un polinomio en su forma factorizada, podemos determinar la multiplicidad de las raíces fácilmente. Simplemente tenemos que contar el número de veces que cada raíz aparece en el polinomio.
Si el polinomio no está en su forma factorizada, necesitamos factorizarlo de ser posible u obtener una gráfica del polinomio para observar su comportamiento al cruzar o topar el eje x.
EJEMPLO
- Encuentra la multiplicidad de las raíces del polinomio $latex {{(x+5)}^2}{{(x-2)}^4}{{(x-3)}^3}$.
Solución: Las raíces del polinomio son $latex x=-5$, $latex x=2$ y $latex x=3$. Para encontrar su multiplicidad, solo tenemos que contar el número de veces que cada raíz aparece. En este caso, la multiplicidad es el exponente al que cada factor está elevado.
- La raíz $latex x=-5$ tiene una multiplicidad de 2.
- La raíz $latex x=2$ tiene una multiplicidad de 4.
- La raíz $latex x=3$ tiene una multiplicidad de 3.
Multiplicidad de raíces de gráficas de polinomios
Las gráficas de polinomios se comportan de diferente manera en varios interceptos en x. Algunas veces, la gráfica cruzará completamente al eje x en un intercepto. Otras veces, la gráfica tocará al eje x y rebotará.
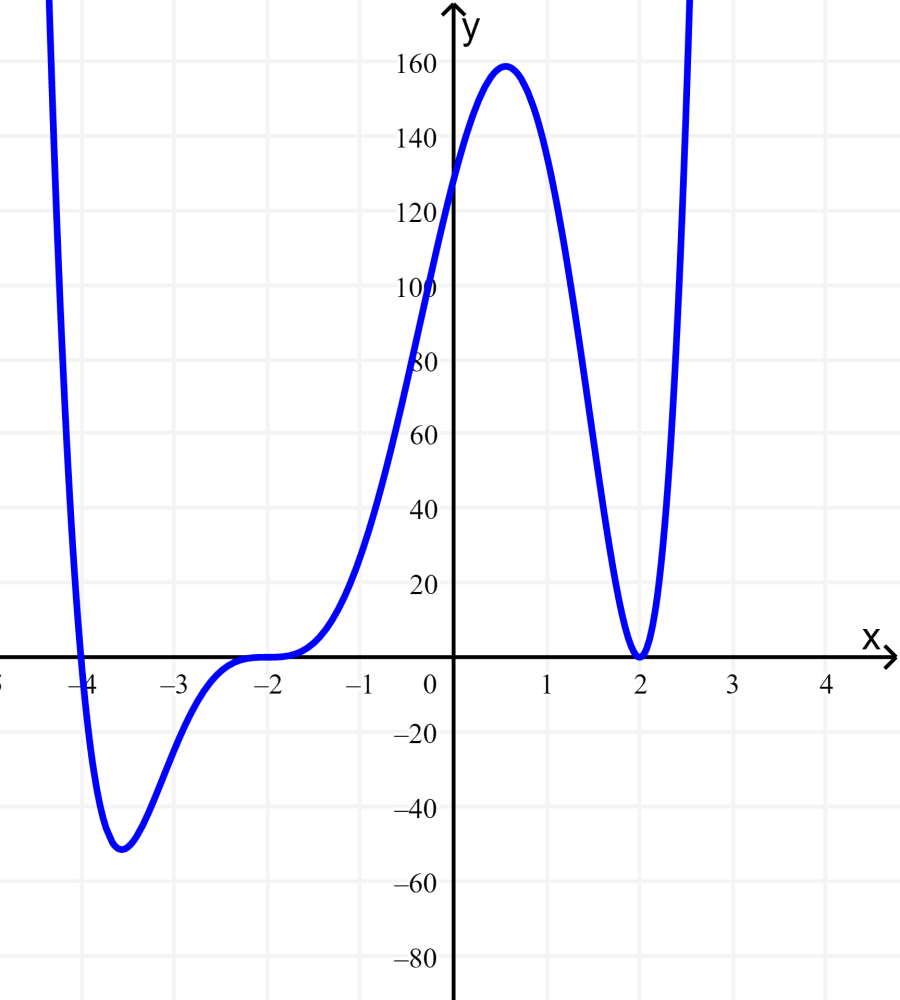
Supongamos que tenemos a la gráfica de la función polinomial $latex f(x)=(x+4){{(x-2)}^2}{{(x+2)}^3}$. Observa que el comportamiento en cada una de las raíces es diferente:
El intercepto en $latex x=-4$ es la solución a la ecuación $latex x+4=0$. La gráfica pasa directamente a través del intercepto en $latex x=-4$. El factor es lineal, por lo que el comportamiento cerca del intercepto es similar a una línea. Esta es una raíz única, ya que la raíz corresponde a un solo factor.
El intercepto en $latex x=2$ es la solución repetida de la ecuación $latex {{(x-2)}^2}=0$. La gráfica toca al eje x en el intercepto y cambia de dirección. El factor es cuadrático, por lo que el comportamiento cerca del intercepto es similar a una cuadrática, es decir, rebota cuando topa al eje x. El factor $latex (x-2)$ aparece dos veces. Entonces, la raíz $latex x=2$ tiene multiplicidad 2.
El intercepto en $latex x=-2$ es la solución repetida del factor $latex {{(x+2)}^3}=0$. La gráfica pasa a través del eje x en el intercepto, pero se aplana un poco al cruzar. Este factor es cúbico, por lo que el comportamiento cerca del intercepto es cúbico, es decir, tiene una forma de S similar a la función $latex f(x)={{x}^3}$. Esta raíz tiene una multiplicidad de 3.
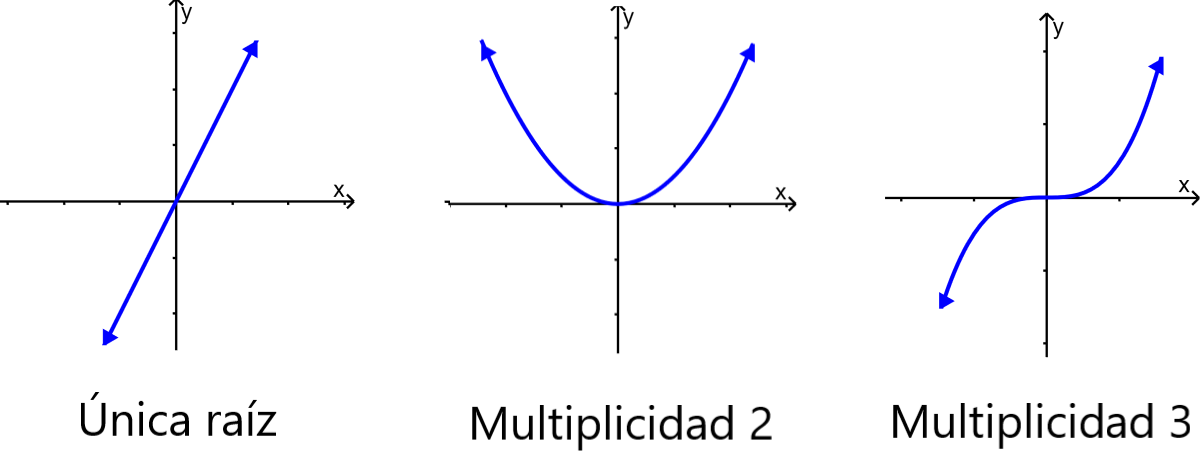
Para las raíces con multiplicidades pares, las gráficas tocan o son tangentes al eje x en estos valores de x. Para las raíces con multiplicidades impares, las gráficas cruzan al eje x en estos valores de x. Las siguientes gráficas ilustran el comportamiento de polinomios con multiplicidad 1, 2 y 3.
Para potencias pares más grandes como 4, 6, 8, la gráfica seguirá tocando al eje x y rebotando, pero con cada incremento de la potencia, la gráfica parecerá aplanarse más y más a medida que se acerca y se aleja del eje x.
De igual forma, para potencias impares más grandes como 5, 7, 9, la gráfica seguirá cruzando al eje x, pero a medida que las potencias incrementan, la gráfica parecerá hacerse más plana a medida que se acerca y se aleja del eje x.
Identificar las raíces y sus multiplicidades usando las gráficas de polinomios
Entonces, resumiendo lo que tenemos arriba, podemos encontrar las multiplicidades de las raíces de polinomios teniendo lo siguiente en mente:
- Si es que la gráfica cruza al eje x y pareciera ser lineal cerca al intercepto, la raíz es única.
- Si es que la gráfica toca al eje x y rebota, la raíz tiene multiplicidad par.
- Si es que la gráfica cruza el eje x en una raíz, entonces, la raíz tiene multiplicidad impar.
- La suma de las multiplicidades es el grado n del polinomio.
Vamos a aplicar estas ideas en el siguiente ejemplo.
EJEMPLO
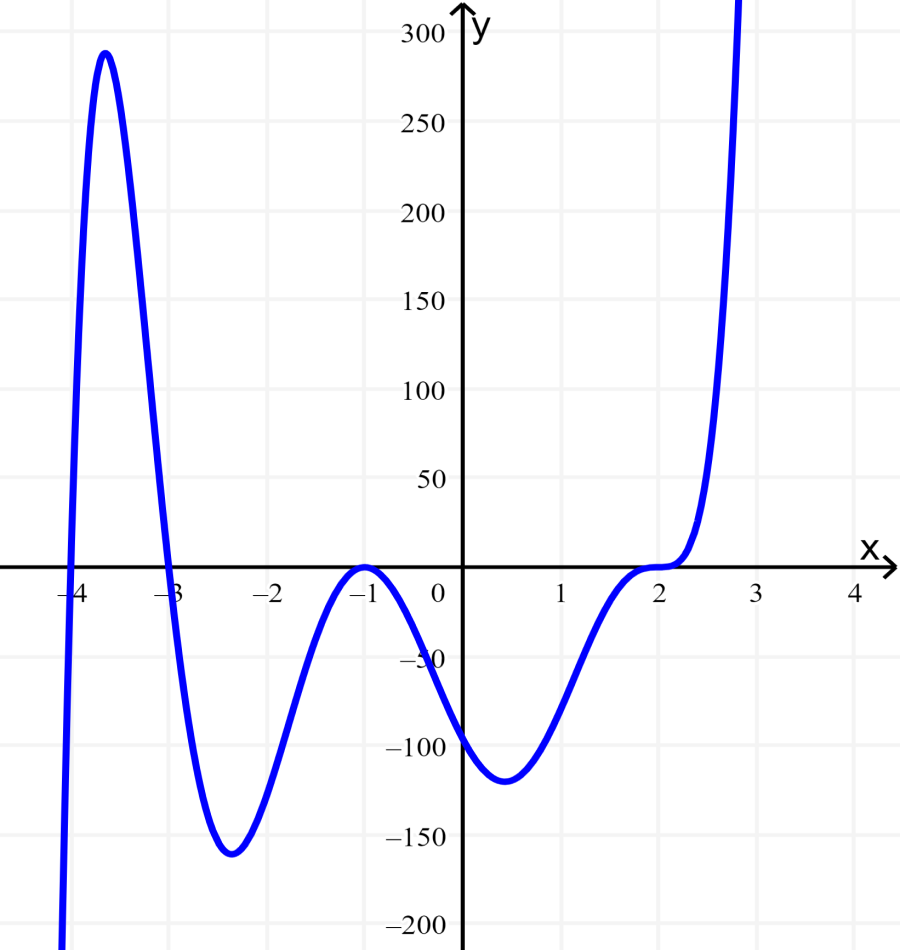
- La siguiente gráfica representa a un polinomio de grado 7. Usa esta gráfica para encontrar las raíces del polinomio y sus posibles multiplicidades.
Solución: La función polinomial es de grado 7, por lo que la suma de las multiplicidades de las raíces debe ser igual a 7.
Empezando desde la izquierda, la primera raíz ocurre en $latex x=-4$. La gráfica se ve casi lineal en ese punto, por lo que sabemos que esta raíz tiene una multiplicidad de 1.
De igual forma, vemos que la raíz que ocurre en $latex x=-3$ también se ve lineal, por lo que esta raíz también tiene una multiplicidad de 1.
Luego, tenemos una raíz en $latex x=-1$. Vemos que en este punto, la gráfica toca al eje x y rebota, por lo que sabemos que la raíz debe tener multiplicidad par. La raíz $latex x=-1$ tiene multiplicidad 2.
El último cero ocurre en $latex x=2$. La gráfica cruza al eje x, por lo que la multiplicidad de esta raíz debe ser impar. Sabemos que la multiplicidad de esta raíz debe ser 3 y la suma de las multiplicidades es igual a 7.
Véase también
¿Interesado en aprender más sobre polinomios? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
