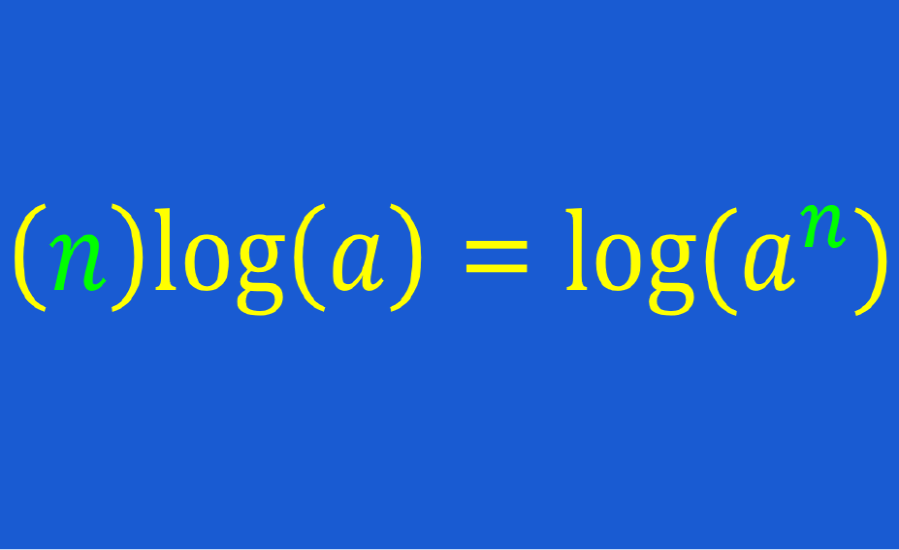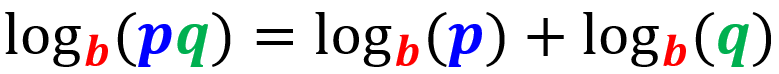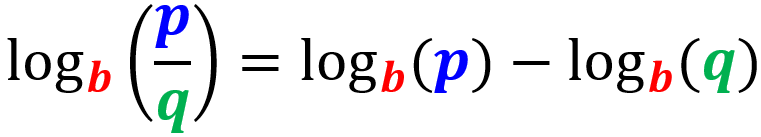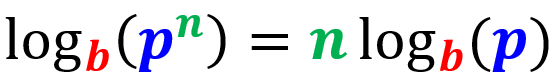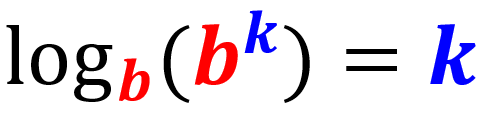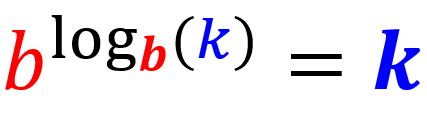Las leyes de los logaritmos nos permiten reescribir a expresiones logarítmicas para formar expresiones más convenientes. Existen siete leyes principales de los logaritmos. Estas siete leyes son útiles para expandir logaritmos, condensar logaritmos y resolver ecuaciones logarítmicas. Las leyes aplican a logaritmos de cualquier base, pero la misma base debe ser usada para aplicar cada ley.
A continuación, conoceremos las leyes principales de los logaritmos. Además, veremos varios ejemplos resueltos para entender cómo aplicar estas leyes para resolver problemas algebraicos.
Descripciones de las leyes de los logaritmos
Recordemos que un logaritmo es la potencia a la que un número debe ser elevado para obtener otro número. Por ejemplo, el logaritmo de base 10 de 100 es 2, ya que 10 elevado a la potencia de 2 es igual a 100:
$latex \log(100)=2$
ya que:
$latex {{10}^2}=100$
La base es el número que está siendo elevado a una potencia. Podemos usar logaritmos con cualquier base. Si quisiéramos, podríamos usar al dos como la base. Por ejemplo, el logaritmo con base dos de ocho es igual a tres ya que dos elevado a la potencia de tres es igual a ocho:
$latex \log_{2}(8)=3$
ya que:
$latex {{2}^3}=8$
Ahora, veamos las leyes de los logaritmos.
Ley 1: Ley del producto
Esta ley nos dice que el logaritmo de un producto es igual a la suma de los logaritmos individuales de los factores:
Ley 2: Ley del cociente
Esta ley nos dice que el logaritmo del cociente de dos cantidades es igual al logaritmo del numerador menos el logaritmo del denominador:
Ley 3: Ley de la potencia
Esta ley nos dice que el logaritmo de un número exponencial es igual al exponente multiplicado por el logaritmo de la base:
Ley 4: Ley del cero
Si es que tenemos el logaritmo de 1 en donde la base es $latex b>0$, pero $latex b\neq 0$, el resultado es igual a cero:
Ley 5: Ley de la identidad
El logaritmo del argumento (dentro del paréntesis), en donde el argumento es igual a la base es igual a 1. Dado que el argumento es igual a la base, b debe ser mayor que cero, pero no puede ser igual a 1:
Ley 6: Ley del logaritmo del exponente
El logaritmo de un número exponencial, en donde su base es la misma que la base del logaritmo es igual al exponente:
Ley 7: Ley del exponente de un logaritmo
Elevar al logaritmo de un número a su base es igual al número:
Ejercicios de leyes de los logaritmos resueltos
Los siguientes ejercicios ponen en práctica las leyes de los logaritmos descritas arriba. Cada ejercicio tiene su respectiva solución para mirar el razonamiento usado y las leyes de los logaritmos aplicadas.
EJERCICIO 1
Evalúa la siguiente expresión: $latex \log_{2}(8)+\log_{2}(4)$.
Solución
Podemos aplicar la regla de producto para obtener:
$latex \log_{2}(8)+\log_{2}(4)=\log_{2}(8\times 4)$
$latex =\log_{2}(32)$
Ahora, podemos escribir a esta expresión en su forma exponencial para obtener el exponente:
$latex 32={{2}^5}$
Entonces, 5 es la respuesta correcta.
EJERCICIO 2
Evalúa la expresión: $latex \log_{3}(162)-\log_{3}(2)$.
Solución
Aquí, tenemos una resta de logaritmos, por lo que podemos aplicar la ley del cociente:
$latex \log_{3}(162)-\log_{3}(2)=\log_{3}(\frac{162}{2})$
$latex =\log_{3}(81)$
Al escribir al argumento en forma exponencial, tenemos:
$latex 81={{3}^4}$
Entonces, la respuesta es 4.
EJERCICIO 3
Calcula el valor de $latex \log_{\sqrt{2}}(64)$.
Solución
Podemos usar la ley de la potencia dos veces para reescribir a la expresión y facilitar la resolución del ejercicio:
$latex \log_{\sqrt{2}}(64)=\log_{\sqrt{2}}{{(2)}^6}$
$latex =6\log_{\sqrt{2}}(2)$
$latex =6\log_{\sqrt{2}}{{(\sqrt{2})}^2}$
$latex =6\times 2\log_{\sqrt{2}}(\sqrt{2})$
$latex =6\times 2(1)$
$latex =12$
EJERCICIO 4
Evalúa la siguiente expresión $$\log_{5}(500)-2\log_{5}(2)+\log_{4}(32)+\log_{4}(8)$$.
Solución
Esta expresión parece un poco complicada a primera vista, pero vemos que tenemos solo logaritmos con dos bases diferentes, 4 y 5.
Entonces, podemos usar la regla del producto para combinar a los logaritmos con base 4 y la regla del cociente para combinar a los logaritmos con base 5. Sin embargo, primero tenemos que aplicar la ley de la potencia al logaritmo con base 5:
$$\log_{5}(500)-2\log_{5}(2)+\log_{4}(32)+\log_{4}(8)$$
$$=\log_{5}(500)-\log_{5}{{(2)}^2}+\log_{4}(32)+\log_{4}(8)$$
$$=\log_{5}(500)-\log_{5}(4)+\log_{4}(32)+\log_{4}(8)$$
$latex =\log_{5}(\frac{500}{4})+\log_{4}(32\times 8)$
$latex =\log_{5}(125)+\log_{4}(256)$
Ahora, podemos reescribir a los argumentos como potencias y aplicamos la ley de la potencia de logaritmos:
$latex =\log_{5}({{5}^3})+\log_{4}({{4}^4})$
$latex =3\log_{5}(5)+4\log_{4}(4)$
$latex =3(1)+4(1)$
$latex =7$
EJERCICIO 5
Evalúa la expresión: $latex 2\log_{3}(5)+\log_{3}(40)-3\log_{3}(10)$.
Solución
Podemos empezar usando la ley de la potencia para reescribir a los logaritmos individuales. Luego, usamos la ley del producto y la ley del cociente:
$latex 2\log_{3}(5)+\log_{3}(40)-3\log_{3}(10)$
$latex =\log_{3}({{5}^2})+\log_{3}(40)-\log_{3}({{10}^3})$
$latex =\log_{3}(25)+\log_{3}(40)-\log_{3}(1000)$
$latex =\log_{3}(\frac{25\times 40}{1000})$
$latex =\log_{3}(1)$
Finalmente, aplicamos la ley del cero para resolver:
$latex \log_{3}(1)=0$
EJERCICIO 6
Expande la expresión logarítmica: $latex \log_{3}(27{{x}^2}{{y}^5})$.
Solución
Tenemos un producto de factores dentro del paréntesis, entonces, podemos aplicar la ley del producto para escribir a cada factor separadamente. Podemos simplificar los logaritmos individuales cuando sea posible.
En este caso, usamos la ley de la identidad para simplificar:
$$\log_{3}(27{{x}^2}{{y}^5})=\log_{3}(27)+\log_{3}({{x}^2})+\log_{3}({{y}^5})$$
$latex =\log_{3}({{3}^3})+\log_{3}({{x}^2})+\log_{3}({{y}^5})$
$latex =3\log_{3}(3)+2\log_{3}(x)+5\log_{3}(y)$
$latex =3(1)+2\log_{3}(x)+5\log_{3}(y)$
$latex =3+2\log_{3}(x)+5\log_{3}(y)$
Ejercicios de leyes de los logaritmos para resolver
Usa las leyes de los logaritmos para resolver los siguientes ejercicios. Escoge una respuesta y verifícala para comprobar que seleccionaste la correcta. Si necesitas ayuda, puedes mirar los ejercicios resueltos de arriba o la lista de las leyes de los logaritmos.
Véase también
¿Interesado en aprender más sobre logaritmos? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
