Para encontrar los puntos de intersección de dos circunferencias, empezamos encontrando la ecuación de la cuerda común. Esto es logrado al restar las ecuaciones de las circunferencias para obtener una ecuación lineal. Luego, sustituimos esta ecuación en una de las ecuaciones de las circunferencias y resolvimos.
A continuación, conoceremos el proceso que podemos usar para encontrar los puntos de intersección de dos circunferencias. Luego, resolveremos algunos ejemplos de práctica.
GEOMETRÍA
Relevante para…
Aprender a encontrar los puntos de intersección de dos circunferencias.
GEOMETRÍA
Relevante para…
Aprender a encontrar los puntos de intersección de dos circunferencias.
Cómo encontrar los puntos de intersección de dos circunferencias
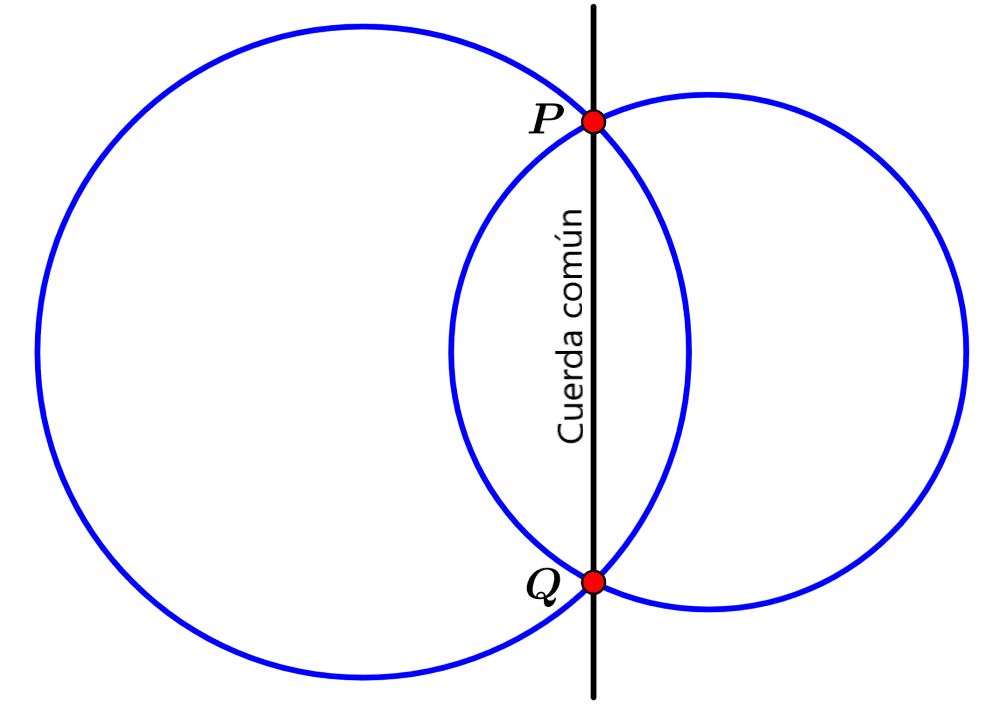
Dos circunferencias pueden intersecar en dos puntos diferentes, como se muestra en el siguiente diagrama:
Las coordenadas de los puntos de intersección, P y Q, satisfacen las ecuaciones de ambas circunferencias. Además, las coordenadas de P y Q también satisfacen la ecuación de la cuerda común.
Considerando esto, podemos encontrar las coordenadas de los puntos de intersección de dos circunferencias, siguiendo los siguientes pasos:
1. Encontrar la ecuación de la cuerda común.
Esta ecuación es una ecuación lineal encontrada al restar a las ecuaciones de las circunferencias, de modo que eliminemos los términos cuadráticos.
2. Resolver la ecuación del paso 1 para una de las variables.
3. Sustituir la ecuación del paso 2 en una de las ecuaciones de las circunferencias.
Al resolver esto, encontraremos ambas coordenadas en x o en y de los puntos.
4. Usar las coordenadas del paso 3 en cualquiera de las ecuaciones de las circunferencias para encontrar las coordenadas faltantes.
Ejercicios resueltos de la intersección de dos circunferencias
EJERCICIO 1
¿Cuáles son las coordenadas de los puntos de intersección de las circunferencias con las ecuaciones $latex x^2+y^2-3x+5y-4=0$ y $latex x^2+y^2-x+4y-7=0$?
Solución
Paso 1: Restando las ecuaciones de las circunferencias, podemos encontrar la ecuación de la cuerda común:
$latex x^2+y^2-3x+5y-4=0$
$latex x^2+y^2-x+4y-7=0~(-$
______________________
$latex -2x+y+3=0$
Paso 2: Resolviendo la ecuación para y, tenemos:
$latex y=2x-3$
Paso 3: Sustituyendo la ecuación del paso 2 en la ecuación de la segunda circunferencia, tenemos:
$latex x^2+y^2-x+4y-7=0$
$$x^2+(2x-3)^2-x+4(2x-3)-7=0$$
$latex 5x^2-5x-10=0$
$latex 5(x-2)(x+1)=0$
Resolviendo, tenemos $latex x=2$ y $latex x=-1$.
Paso 4: Cuando $latex x=2$, tenemos $latex y=1$ y cuando $latex x=-1$, tenemos $latex y=-5$.
Entonces, los puntos de intersección de las circunferencias son $latex (-1,~-5)$ y $latex (2, 1)$.
EJERCICIO 2
Determina las coordenadas de los puntos de intersección de las circunferencias con las ecuaciones $latex x^2+y^2-5x+3y-4=0$ y $latex x^2+y^2-4x+6y-12=0$.
Solución
Paso 1: Al restar las ecuaciones de las circunferencias, tenemos:
$latex x^2+y^2-5x+3y-4=0$
$latex x^2+y^2-4x+6y-12=0~(-$
______________________
$latex -x-3y+8=0$
Paso 2: Resolviendo la ecuación para x, tenemos:
$latex x=-3y+8$
Paso 3: Sustituyendo la ecuación del paso 2 en la ecuación de la primera circunferencia, tenemos:
$latex x^2+y^2-5x+3y-4=0$
$$(-3y+8)^2+y^2-5(-3y+8)+3y-4=0$$
$latex 10y^2-30y+20=0$
$latex 10(y-2)(y-1)=0$
Resolviendo, tenemos $latex y=2$ y $latex y=1$.
Paso 4: Cuando $latex y=2$, tenemos $latex x=2$ y cuando $latex y=1$, tenemos $latex x=5$.
Entonces, los puntos de intersección de las circunferencias son $latex (2, ~2)$ y $latex (5,~ 1)$.
EJERCICIO 3
¿Cuáles son los puntos de intersección de las circunferencias $latex x^2+y^2-4x+3y+5=0$ y $latex x^2+y^2-6x+5y+9=0$?
Solución
Paso 1: Vamos a encontrar la ecuación de la cuerda común al restar las ecuaciones de las circunferencias:
$latex x^2+y^2-4x+3y+5=0$
$latex x^2+y^2-6x+5y+9=0~(-$
______________________
$latex 2x-2y-4=0$
Paso 2: Podemos simplificar la ecuación obtenida al dividir por 2, y al resolver para x, tenemos:
$latex x-y-2=0$
$latex x=y-2$
Paso 3: Vamos a sustituir la ecuación del paso 2 en la ecuación de la primera circunferencia. Entonces, tenemos:
$latex x^2+y^2-4x+3y+5=0$
$$(y-2)^2+y^2+4(y-2)+3y+5=0$$
$latex 2y^2+3y+1=0$
$latex (2y+1)(y+1)=0$
Resolviendo, tenemos $latex y=-\frac{1}{2}$ y $latex y=-1$.
Paso 4: Cuando $latex y=-\frac{1}{2}$, tenemos $latex x=1~\frac{1}{2}$ y cuando $latex y=-1$, tenemos $latex x=1$.
Entonces, los puntos de intersección de las circunferencias son $latex (1 ~\frac{1}{2},~-\frac{1}{2})$ y $latex (1, -1)$.
EJERCICIO 4
Encuentra las coordenadas de los puntos de intersección de las circunferencias $latex x^2+y^2+3x-2y-7=0$ y $latex x^2+y^2+x-y-8=0$.
Solución
Paso 1: Restando las ecuaciones de las circunferencias, tenemos:
$latex x^2+y^2+3x-2y-7=0$
$latex x^2+y^2+x-y-8=0~(-$
______________________
$latex 2x-y+1=0$
Paso 2: Resolviendo la ecuación para y, tenemos:
$latex y=2x+1$
Paso 3: Usando la ecuación del paso 2 en la ecuación de la segunda circunferencia, tenemos:
$latex x^2+y^2+x-y-8=0$
$$x^2+(2x+1)^2+x-(2x+1)-8=0$$
$latex 5x^2+3x-8=0$
$latex (5x+8)(x-1)=0$
Resolviendo, tenemos $latex x=-\frac{8}{3}$ y $latex x=1$.
Paso 4: Cuando $latex x=-\frac{8}{3}$, tenemos $latex y=-\frac{11}{5}$ y cuando $latex x=1$, tenemos $latex y=3$.
Entonces, los puntos de intersección de las circunferencias son $latex (-\frac{8}{3},~\frac{11}{5})$ y $latex (1, 3)$.
EJERCICIO 5
Encuentra las coordenadas de los puntos de intersección de las circunferencias con las ecuaciones $latex x^2+y^2-3x+13y-48=0$ y $latex x^2+y^2+x-3y=0$.
Solución
Paso 1: Encontramos la ecuación de la cuerda común al restar a las ecuaciones de las circunferencias:
$latex x^2+y^2-3x+13y-48=0$
$latex x^2+y^2+x-3y=0~~(-$
______________________
$latex -4x+16y-48=0$
Paso 2: Podemos simplificar la ecuación obtenida al dividir por 4, y al resolver para x, tenemos:
$latex -x+4y-12=0$
$latex x=4y-12$
Paso 3: Sustituyendo la ecuación del paso 2 en la ecuación de la segunda circunferencia, tenemos:
$latex x^2+y^2+x-3y=0$
$$(4y-12)^2+y^2+(4y-12)-3y=0$$
$latex 17y^2-95y+132=0$
$latex (17y-44)(y-3)=0$
Resolviendo, tenemos $latex y=\frac{44}{17}$ y $latex y=3$.
Paso 4: Cuando $latex y=\frac{44}{17}$, tenemos $latex x=-\frac{28}{17}$ y cuando $latex y=3$, tenemos $latex x=0$.
Entonces, los puntos de intersección de las circunferencias son $latex (-\frac{28}{17},~\frac{44}{17})$ y $latex (0, 3)$.
Intersección de dos circunferencias – Ejercicios para resolver
Las circunferencias $latex x^2-10x+y^2-8y+36=0$ y $latex x^2-2x+y^2-12y+32=0$ tienen un solo punto de intersección.
Escribe las coordenadas del punto en la casilla.
Véase también
¿Interesado en aprender más sobre círculos? Puedes mirar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
