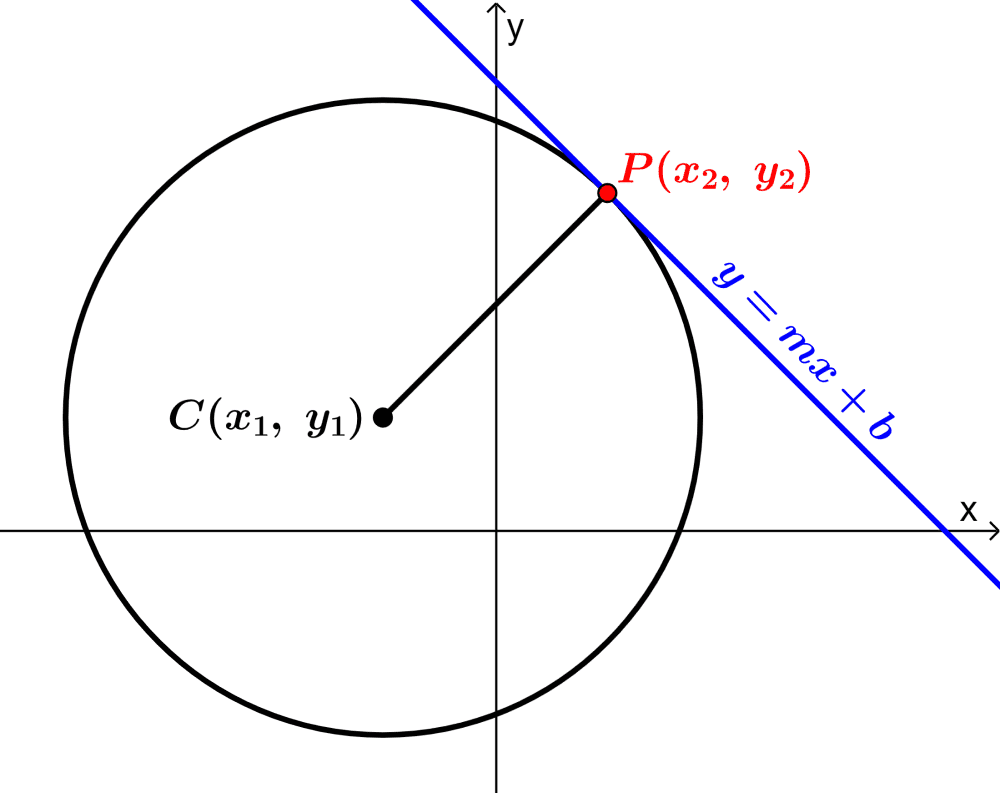
La ecuación de la recta tangente a un círculo es encontrada usando la forma y=mx+b. A su vez, podemos encontrar la pendiente m al determinar la pendiente del radio con el centro del círculo y el punto tangente. Luego, usamos el punto tangente para encontrar el valor de b.
A continuación, aprenderemos cómo encontrar la ecuación de la tangente a un círculo paso a paso. Luego, aplicaremos este proceso para resolver algunos ejercicios de práctica.
GEOMETRÍA
Relevante para…
Aprender a encontrar la ecuación de la tangente a un círculo.
GEOMETRÍA
Relevante para…
Aprender a encontrar la ecuación de la tangente a un círculo.
Cómo encontrar la ecuación de la recta tangente a un círculo
Para encontrar la ecuación de la tangente a un círculo, recordamos que podemos encontrar la ecuación de cualquier recta usando la forma $latex y=mx+b$, en donde m es la pendiente y b es el intercepto en y.
En este caso, la pendiente m es encontrada usando la pendiente del radio y el intercepto en y es encontrado usando las coordenadas del punto tangencial.
Entonces, seguimos los siguientes pasos:
1. Encontrar las coordenadas del centro del círculo.
Si es que la ecuación está dada en su forma estándar, $latex r^2=(x-a)^2+(x-b)^2$, el centro es $latex (a,~b)$. Si es que tenemos una ecuación general del círculo, tenemos que completar el cuadrado para encontrar el centro.
2. Encontrar la pendiente del radio del círculo.
Para esto, usamos la fórmula de la pendiente $latex m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$ con las coordenadas del punto tangencial y el centro del círculo.
3. Encontrar la pendiente de la recta tangente.
Dado que el radio y la tangente son perpendiculares, la pendiente de la tangente es igual al recíproco negativo de la pendiente del radio.
4. Encontrar el valor de b, el intercepto en y.
Para esto, usamos la pendiente del paso 3 y las coordenadas del punto tangencial en la forma $latex y=mx+b$ y resolvemos para b.
Ejercicios resueltos de la ecuación de la tangente a un círculo
EJERCICIO 1
Encuentra la ecuación de la recta tangente al círculo $latex (x+2)^2+(y-3)^2=4$ en el punto $latex P=(0,~4)$.
Solución
Paso 1: Dado que la ecuación del círculo está en forma estándar, podemos fácilmente ver que el centro es igual a $latex (-2, 3)$.
Paso 2: Usamos $latex (x_{1},~y_{1})=(-2, 3)$ y $latex (x_{2},~y_{2})=(0, ~4)$ para encontrar la pendiente del radio del círculo:
$$m_{r}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$$
$$=\frac{4-3}{0+2}$$
$$=\frac{1}{2}$$
Paso 3: La pendiente de la recta tangente es:
$$m=-\frac{1}{m_{r}}$$
$$m=-2$$
Paso 4: Para encontrar el valor de b, usamos $latex (x,~y)=(0,~4)$:
$latex y=mx+b$
$latex 4=-2(0)+b$
$latex b=4$
La ecuación de la recta tangente al círculo en $latex (0, ~4)$ es $latex y=-2x+4$.
EJERCICIO 2
¿Cuál es la ecuación de la recta tangente al círculo $latex (x-1)^2+(y-2)^2=10$ en el punto $latex P=(4,~3)$?
Solución
Paso 1: Tenemos a la ecuación del círculo en su forma estándar, por lo que vemos que el centro es $latex (1, 2)$.
Paso 2: Encontramos la pendiente del radio del círculo usando las coordenadas $latex (x_{1},~y_{1})=(1, 2)$ y $latex (x_{2},~y_{2})=(4, ~3)$ para encontrar la pendiente del radio del círculo:
$$m_{r}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$$
$$=\frac{3-2}{4-1}$$
$$=\frac{1}{3}$$
Paso 3: La pendiente de la recta tangente es:
$$m=-\frac{1}{m_{r}}$$
$$m=-3$$
Paso 4: Usando el punto tangencial $latex (x,~y)=(4,~3)$, encontramos el valor de b:
$latex y=mx+b$
$latex 3=-3(4)+b$
$latex b=15$
La ecuación de la recta tangente al círculo en $latex (4, ~3)$ es $latex y=-3x+15$.
EJERCICIO 3
Encuentra la ecuación de la recta tangente al círculo $latex x^2+y^2+2x-4y-20=0$ en el punto $latex P=(2, 6)$.
Solución
Paso 1: En este caso, la ecuación del círculo está en su forma general. Entonces, la escribimos en su forma estándar al completar el cuadrado de ambas variables:
$latex x^2+y^2+2x-4y-20=0$
$latex x^2+2x+y^2-4y-20=0$
$$(x+1)^2-1+(y-2)^2-4-20=0$$
$latex (x+1)^2+(y-2)^2=25$
Ahora, vemos que el centro es $latex (-1, ~2)$.
Paso 2: La pendiente del radio del círculo es:
$$m_{r}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$$
$$=\frac{6-2}{2+1}$$
$$=\frac{4}{3}$$
Paso 3: La pendiente de la recta tangente es:
$$m=-\frac{1}{m_{r}}$$
$$m=-\frac{3}{4}$$
Paso 4: Para encontrar el valor de b, usamos las coordenadas del punto tangencial $latex (x,~y)=(2,~6)$:
$latex y=mx+b$
$latex 6=-\frac{3}{4}(2)+b$
$latex b=\frac{15}{2}$
La ecuación de la recta tangente al círculo en $latex (2, ~6)$ es $latex y=-\frac{3}{4}x+\frac{15}{2}$.
EJERCICIO 4
¿Cuál es la ecuación de la recta tangente al círculo $latex x^2+y^2-2x-6y+8=0$ en el punto $latex P=(2, 2)$?
Solución
Paso 1: Escribiendo a la ecuación del círculo en su forma estándar, tenemos:
$latex x^2+y^2-2x-6y+8=0$
$latex x^2-2x+y^2-6y+8=0$
$$(x-1)^2-1+(y-3)^2-9+8=0$$
$latex (x-1)^2+(y-3)^2=2$
El centro del círculo es $latex (1, ~3)$.
Paso 2: Encontrando la pendiente del radio del círculo, tenemos:
$$m_{r}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$$
$$=\frac{2-3}{2-1}$$
$latex =-1$
Paso 3: La pendiente de la recta tangente es:
$$m=-\frac{1}{m_{r}}$$
$$m=1$$
Paso 4: Usamos al punto tangencial para encontrar el valor de b:
$latex y=mx+b$
$latex 2=1(2)+b$
$latex b=0$
La ecuación de la recta tangente al círculo en $latex (2, ~2)$ es $latex y=x$.
EJERCICIO 5
Encuentra la ecuación de la recta tangente al círculo $latex x^2+y^2+4x+6y-21=0$ en el punto $latex P=(1, ~2)$.
Solución
Paso 1: Encontrando la forma estándar de la ecuación del círculo dado, tenemos:
$latex x^2+y^2+4x+6y-21=0$
$latex x^2+4x+y^2+6y-21=0$
$$(x+2)^2-4+(y+3)^2-9-21=0$$
$latex (x+2)^2+(y+3)^2=34$
El centro del círculo es $latex (-2,~-3)$.
Paso 2: Encontrando la pendiente del radio del círculo, tenemos:
$$m_{r}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$$
$$=\frac{2+3}{1+2}$$
$$=\frac{5}{3}$$
Paso 3: La pendiente de la recta tangente es:
$$m=-\frac{1}{m_{r}}$$
$$m=-\frac{3}{5}$$
Paso 4: Usamos $latex (x,~y)=(1,~2)$ para encontrar el valor de b:
$latex y=mx+b$
$latex 2=-\frac{3}{5}(1)+b$
$latex b=\frac{13}{5}$
La ecuación de la recta tangente al círculo en $latex (1, ~2)$ es $latex y=-\frac{3}{5}x+\frac{13}{5}$.
EJERCICIO 6
¿Cuál es la ecuación de la recta tangente al círculo $latex x^2+y^2+6x-4y+8=0$ en el punto $latex P=(-1, 1)$?
Solución
Paso 1: Escribiendo a la ecuación del círculo en su forma estándar, tenemos:
$latex x^2+y^2+6x-4y+8=0$
$latex x^2+6x+y^2-4y+8=0$
$$(x+3)^2-9+(y-2)^2-4+8=0$$
$latex (x+3)^2+(y-2)^2=5$
Ahora, vemos que el centro del círculo es $latex (-3, ~2)$.
Paso 2: La pendiente del radio del círculo es:
$$m_{r}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$$
$$=\frac{1-2}{-1+3}$$
$$=-\frac{1}{2}$$
Paso 3: La pendiente de la recta tangente es:
$$m=-\frac{1}{m_{r}}$$
$latex m=2$
Paso 4: Para encontrar el valor de b, usamos $latex (x,~y)=(-1,~1)$:
$latex y=mx+b$
$latex 1=2(-1)+b$
$latex b=3$
La ecuación de la recta tangente al círculo en $latex (-1, ~1)$ es $latex y=2x+3$.
Ecuación de la tangente a un círculo – Ejercicios para resolver
Encuentra la ecuación de la tangente al siguiente círculo en el punto (1, 4):$$ x^2-6x+y^2-6y+18=5$$
Escribe la ecuación en la casilla.
Véase también
¿Interesado en aprender más sobre círculos? Puedes mirar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
